DeepFool对抗算法_学习笔记

前言

本篇博客出于学习交流目的，主要是用来记录自己学习中遇到的问题和心路历程，方便之后回顾。过程中可能引用其他大牛的博客，文末会给出相应链接，侵删！

---

DeepFool算法
特点：提出鲁棒性评估指标
论文原文：DeepFool: a simple and accurate method to fool deep neural networks

正文

之前的博客讲了FGSM算法，但是有人可能会有疑问，怎么确定 ε ε 的大小，取值大小这会对算法效果产生很大影响，那么今天的这个算法可以避免这个问题。
文章首次提出了一个分类器鲁棒性的评估指标：
图像样本： x x ， x∈Rn x ∈ R n
分类器： k^(x) k ^ ( x )
对抗扰动： r r
分类器在 x x 处的鲁棒性 Δ(x;k^) Δ ( x ; k ^ ) ：

Δ(x;k^):=minr||r||2  s.t.k^(x+r)≠k^(x) Δ ( x ; k ^ ) := min r | | r | | 2     s . t . k ^ ( x + r ) ≠ k ^ ( x )

即x到分类边界的距离，下文会更详细理解。

分类器 k^(x) k ^ ( x ) 的鲁棒性：

ρadv(k^)=ExΔ(x;k^)||x||2 ρ a d v ( k ^ ) = E x Δ ( x ; k ^ ) | | x | | 2

样本离分类边界越远，样本2范数越小，评测数值越大表示越鲁棒。

---

我们先从二分类器看，多分类器可以看做是多个二分类器的共同作用。
二分类问题
二分类器： k^(x)=sign(wTx+b):=sign(f(x)) k ^ ( x ) = s i g n ( w T x + b ) := s i g n ( f ( x ) )
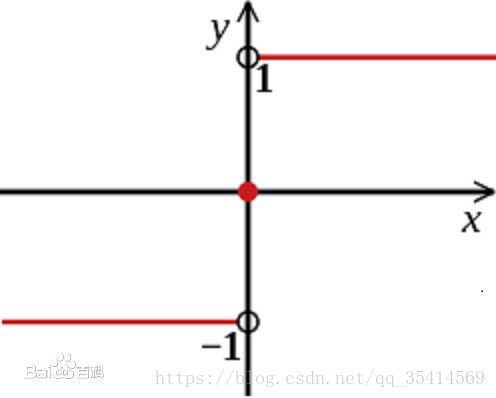图为sign()函数

分类边界： F={x:f(x)=0} F = { x : f ( x ) = 0 } ，分界线两边分别为正负类
扰动向量：
r⋆(x0):=argminr||r||2 r ⋆ ( x 0 ) := arg ⁡ min r | | r | | 2
s.t. sign(f(x0+r))≠sign(f(x0)) s . t .   s i g n ( f ( x 0 + r ) ) ≠ s i g n ( f ( x 0 ) )
=−f(x0)||w||22w = − f ( x 0 ) | | w | | 2 2 w

借助原文中的图例来看公式可以很好理解

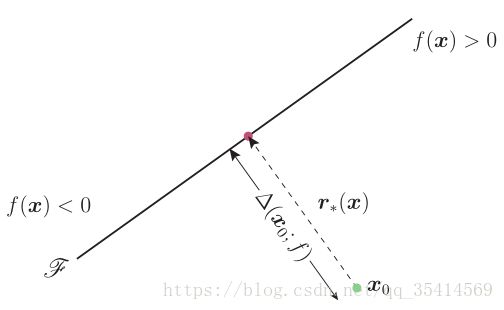
其实这个公式可以理解为样本到分类边界的最短距离 f(x0)∥w∥2 f ( x 0 ) ‖ w ‖ 2 乘上法线方向的单位向量 w∥w∥2 w ‖ w ‖ 2 ,因为始终指向分类边界方向，所以有个负号。

如果是迭代算法，那么扰动计算公式将变为：

argrimin∥ri∥2 subject to f(xi)+▽f(xi)Tri=0 a r g r i m i n ‖ r i ‖ 2   s u b j e c t   t o   f ( x i ) + ▽ f ( x i ) T r i = 0

多分类问题
类标数： c c ，即映射空间 Rn→Rc R n → R c
分类函数： f(x)=WTx+b f ( x ) = W T x + b
分类器： k^(x)=argmaxkfk(x) k ^ ( x ) = arg ⁡ max k f k ( x ) ， fk(x) f k ( x ) 是向量 f(x) f ( x ) 的第 k k 个维度，也可看做是第 k k 个子分类器。
扰动向量：
argminr||r||2 arg ⁡ min r | | r | | 2
s.t.∃k:wTk(x0+r)+bk≥wTk^(x0)(x0+r)+bk^(x0) s . t . ∃ k : w k T ( x 0 + r ) + b k ≥ w k ^ ( x 0 ) T ( x 0 + r ) + b k ^ ( x 0 )
其中 wk w k 是 W W 的第 k k 列，即第 k k 个子分类器的权值向量。
要使得分类结果改变，必须保证至少存在一个非原始类标的分类器结果大于原始分类函数结果。
第 k k 个分类边界： Fk={x:fk(x)−fk^(x0)(x)=0} F k = { x : f k ( x ) − f k ^ ( x 0 ) ( x ) = 0 }
x0 x 0 与所在的凸区域可由超平面 P P 围成：

P=⋂k=1c{x:fk^(x0)(x)≥fk(x)} P = ⋂ k = 1 c { x : f k ^ ( x 0 ) ( x ) ≥ f k ( x ) }

这时候我们需要得到一个点到某分类函数边界的最小距离，即：

l^(x0)=argmink≠k^(x0)|fk(x0)−fk^(x0)(x0)|||wk−wk^(x0)||2 l ^ ( x 0 ) = arg ⁡ min k ≠ k ^ ( x 0 ) | f k ( x 0 ) − f k ^ ( x 0 ) ( x 0 ) | | | w k − w k ^ ( x 0 ) | | 2

同样用原文的图来帮助理解：

假设有4个类， x0 x 0 属于原本第4类，那么我们可以根据 Fk={x:fk(x)−f4(x)=0} F k = { x : f k ( x ) − f 4 ( x ) = 0 } 确定一个超平面如图绿线围成。然后计算分别距离各个分类器的最小距离。

那么我们就得到最小扰动 r⋆(x0) r ⋆ ( x 0 ) ：

r⋆(x0)=|fl^(x0)(x0)−fk^(x0)(x0)|||wl^(x0)−wk^(x0)||22(wl^(x0)−wk^(x0)) r ⋆ ( x 0 ) = | f l ^ ( x 0 ) ( x 0 ) − f k ^ ( x 0 ) ( x 0 ) | | | w l ^ ( x 0 ) − w k ^ ( x 0 ) | | 2 2 ( w l ^ ( x 0 ) − w k ^ ( x 0 ) )

如果是迭代则公式变为如下：

P=⋂k=1c{x:fk(xi)−fk^(x0)(xi)+▽fk(xi)⊤x−▽fk^(x0)(xi)⊤x≤0} P = ⋂ k = 1 c { x : f k ( x i ) − f k ^ ( x 0 ) ( x i ) + ▽ f k ( x i ) ⊤ x − ▽ f k ^ ( x 0 ) ( x i ) ⊤ x ≤ 0 }

小结

由线性推广到非线性也一样，文章还给出了由2范数推广到 lp l p 范数，以及和FGSM算法的实验对比，有兴趣的可以详细看原文。

代码

在cleverhans团队给的demo上修改了一下，可以下载运行mnist数据集进行测试，如果想测试其他数据集或者有任何问题，我们都可以随时探讨。在原库中有些bug或者版本兼容问题已经修改，utils_tf.py中训练是可能会遇到shape不匹配问题。将输入reshape一下就可以了。
下载地址：DeepFool对抗算法
注：依赖cleverhans集成库，或是我资源中的FGSM算法也可以。
cleverhans_github地址：https://github.com/tensorflow/cleverhans