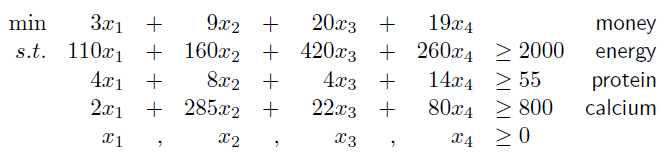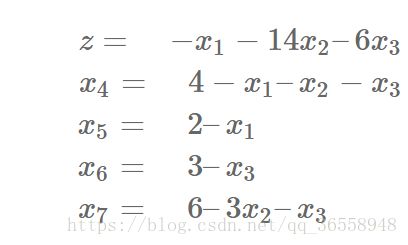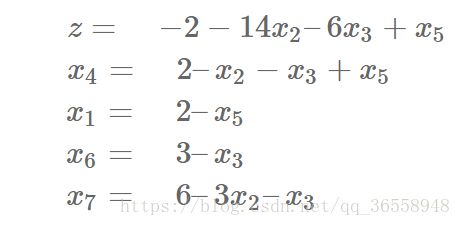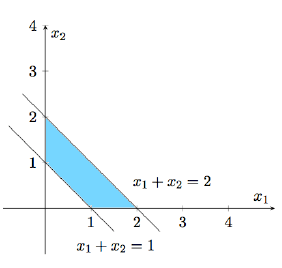线性规划-单纯形算法详解

本博客若无特殊说明则由 hrwhisper 原创发布
转载请点名出处：细语呢喃 > 线性规划-单纯形算法详解
本文地址：https://www.hrwhisper.me/introduction-to-simplex-algorithm

线性规划-单纯形算法详解

 2016年11月24日   hrwhisper  7 Comments 15,246 views

本文将详细的介绍单纯形算法，包括但不限于

• LP问题
• 单纯形算法原理
• 无界、无解、循环等情况
• python代码实现

线性规划问题

首先引入如下的问题：

假设食物的各种营养成分、价格如下表：

Food	Energy（能量）	Protein（蛋白质）	Calcium（钙）	Price
Oatmeal（燕麦）	110	4	2	3
Whole milk（全奶）	160	8	285	9
Cherry pie（草莓派）	420	4	22	20
Pork with beans（猪肉）	260	14	80	19

要求我们买的食物中，至少要有2000的能量，55的蛋白质，800的钙，怎样买最省钱？

设买燕麦、全奶、草莓派、猪肉为x1,x2,x3,x4

于是我们可以写出如下的不等式组

其实这些不等式组就是线性规划方程（Linear programming formulation）：

简单的说，线性规划就是在给定限制的情况下，求解目标。

可行域

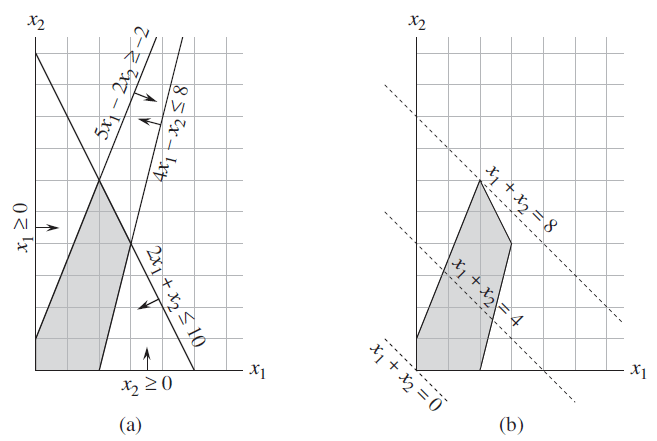
来看一个算法导论中的例子，考虑如下的线性规划：

maxs.t.x1+x24x1–x22x1+x25x1–2x2x1,x2≤≤≥≥810−20

我们可以画出下面的图：

看图a，灰色的区域就是这几个约束条件要求x1,x2所在的区域，而我们最后的解x1,x2也要在这里面。我们把这个区域称为可行域（feasible region）

图b可以直观的看出，最优解为8, 而 x1= 2 , x2=6

 

线性规划标准形式

线性规划的标准形式如下：

mins.t.AxxcTx≤b≥0

 

就是

• 求的是min（算法导论的是max，本文为min）
• 所有的约束为<=的形式
• 所有的变量均 >=0

如何变为标准形式？

• 原来是max, 直接*-1求min
• 若原来约束为=，转为 >= 和<=
• 约束原来为 >= 同样的*-1，就改变了<=
• 若有变量 xi < 0 ，那么用 x‘ – x”来替代，其中 x’>=0 x”>=0

 

线性规划松弛形式

松弛形式为：

mins.t.AxxcTx=b≥0

就是通过引入变量把原来的 <= ，变为=的松弛形式.

如：

x1+x2x1+x2x1,x2≤2≥1≥0

写为松弛形式就是

x1+x2+x3x1+x2+x4x1,x2,x3,x4=2=1≥0

<= vs <

有砸场子的同学会问(╯‵□′)╯︵┻━┻，为什么我们的线性规划的形式都是可以 <= 或者 >=的形式的？把等号去掉可以么？

就是不可以(￣ε(#￣)

举个例子

maxs.t.xx≤1

maxs.t.xx<1

显然第二个是无解的。

 

单纯形算法的思想与例子

如何求解线性规划问题呢？

有一些工具如GLPK，Gurobi 等，不在本文的介绍范围内。

本文要介绍的是单纯形算法，它是求解线性规划的经典方法，虽然它的执行时间在最坏的情况下是非多项式的（指数时间复杂度），但是，在绝大部分情况下或者说实际运行过程中却是多项式时间。

它主要就三个步骤

1. 找到一个初始的基本可行解
2. 不断的进行旋转（pivot）操作
3. 重复2直到结果不能改进为止

以下面的线性规划为例:

mins.t.−x1x1x1x1−+,14x2x23x2x2−++,6x3x3x3x3x3≤≤≤≤≥42360

将其写为松弛的形式：

mins.t.−x1−14x2–6x3x1+x2+x3+x4x1+x5x3++x63x2+x3+x7x1,x2,x3,x4,x5,x6,x7====≥04236

其实，就是等价于（仍然要求 x1,x2,x3,x4,x5,x6,x7 >=0）：

z=−x1−14x2–6x3x4=4−x1–x2−x3x5=2–x1x6=3–x3x7=6–3x2–x3

在上述的等式的左边称为基本变量，而右边称为非基本变量。

现在来考虑基本解就是把等式右边的所有非基本变量设为0，然后计算左边基本变量的值。

这里，容易得到基本解为：(x1,x2….x7) = (0,0,0,4,2,3,6)，而目标值z = 0，其实就是把基本变量xi设置为bi。

一般而言，基本解是可行的，我们称其为基本可行解。初始的基本解不可行的情况见后面的讨论，这里假设初始的基本解就是基本可行解，因此三个步骤中第一步完成了。

现在开始，来讨论上面的第二个步骤，就是旋转的操作。

我们每次选择一个在目标函数中的系数为负的非基本变量xe，然后尽可能的增加xe而不违反约束，并将xe用基本变量xl表示， 然后把xe变为基本变量，xl变为非基本变量。

这里，假设我们选择增加x1，那么在上述的等式（不包括目标函数z那行）中，第1个等式限制了x1 <=4（因为x4>=0），第2个等式有最严格的限制，它限制了x1 <=2，因此我们最多只能将x1增加到2，根据上面的第二个等式，我们有： x1 = 2 – x5，带入上面的等式就实现了xe和xl的替换：

z=−2−14x2–6x3+x5x4=2–x2−x3+x5x1=2–x5x6=3–x3x7=6–3x2–x3

这样其实就是一个转动(pivot)的过程，一次转动选取一个非基本变量（也叫替入变量）xe 和一个基本变量（也叫替出变量） xl ，然后替换二者的角色。执行一次转动的过程与之前所描述的线性规划是等价的。

同样的，将非基本变量设为0，于是得到：(x1,x2….x7) = (2,0,0,2,0,3,6)， Z = -2，说明我们的目标减少到了-2

接下来是单纯形算法的第三步，就是不断的进行转动，直到无法进行改进为止，继续看看刚才的例子：

我们接着再执行一次转动，这次我们可以选择增大x2或者x3，而不能选择x5，因为增大x5之后，z也增大，而我们要求的是最小化z。假设选择了x2，那么第1个等式限制了x2 <=2 , 第4个等式限制了x2 <= 2，假设我们选择x4为替出变量，于是有： x2 = 2 – x3 – x4 + x5 ，带入得：

z=−30+8x3+14x4−13x5x2=2−x3−x4+x5x1=2–x5x6=3–x3x7=2x3+3x4–3x5

此时，我们的基本解变为(x1,x2….x7) = (2,2,0,0,0,3,0)， Z = -30

我们可以继续的选择增大x5，第4个等式具有最严格的限制（0 – 3x5 >=0），我们有x5 = 2/3 x3 + x4 – 1/3 x7

带入得

z=−30–23x3+x4+133x7x2=2–13x3−13x7x1=2–23x3–x4+13x7x6=3–x3x5=23x3+x4–13x7

此时，我们的基本解变为(x1,x2….x7) = (2,2,0,0,0,3,0)， Z = -30，这时候并没有增加，但是下一步，我们可以选择增加 x3。第2个和第3个有最严格的限制，我们选第2个的话，得：x3 = 3 – 3/2 x1 – 3/2 x4 + 1/2 x7，然后老样子，继续带入：

z=−32+x1+2x4+4x7x2=1+12x1+12x4–12x7x3=3–32x1–32x4+12x7x6=32x1+32x4–12x7x5=2–x1

现在，已经没有可以继续增大的值了，停止转动，z=-32就是我们的解，而此时，基本解为：(x1,x2….x7) = (0,1,3,0,2,0,0)，看看最开始的目标函数：z = -x1 -14x2 – 6x3 ,我们将x2=1,x3=3带入得，z=-32，说明我们经过一系列的旋转，最后得到了目标值。

 

退化(Degeneracy)

在旋转的过程中，可能会存在保持目标值不变的情况，这种现象称为退化。比如上面的例子中，两次等于-30.

可以说退化可能会导致循环（cycling）的情况，这是使得单纯形算法不会终止的唯一原因。还好上面的例子中，我们没有产生循环的情况，再次旋转，目标值继续降低。

《算法导论》是这样介绍退化产生循环的：

Degeneracy can prevent the simplex algorithm from terminating, because it can lead to a phenomenon known as cycling: the slack forms at two different iterations of SIMPLEX are identical. Because of degeneracy, SIMPLEX could choose a sequence of pivot operations that leave the objective value unchanged but repeat a slack form within the sequence. Since SIMPLEX is a deterministic algorithm, if it cycles, then it will cycle through the same series of slack forms forever, never terminating.

如何避免退化？一个方法就是使用Bland规则：

在选择替入变量和替出变量的时候，我们总是选择满足条件的下标最小值。

• 替入变量xe：目标条件中，系数为负数的第一个作为替入变量
• 替出变量xl：对所有的约束条件中，选择对xe约束最紧的第一个

在上面的例子中，我也是这么做的。^ ^

另一个方法是加入随机扰动。

 

无界(unbounded)的情况

有的线性规划问题是无界的，举个栗子

对于下面的线性规划

mins.t.−−x1–x2x1–x2x1+x2x1,x2≤1≤1≥0

画出区域为：

显然可以不断的增大。让我们来看看单纯形算法是如何应对的：

上述的写成松弛形式为：

mins.t.−−x1–x2x1–x2+x1+x2x1,x2,x3,x4≥0x3+x4=1=1

也就是，

zx3x4===−x1–x21–x1+x21+x1–x2

选择x1 为替入变量，x3为替出变量，有：

zx1x4===−1–2x2+x31+x2–x32–x3

这时候我们只能选择x2 为替入变量,才能使得目标值变小，但是我们发现，对于x2没有任何的约束，也就是说，x2可以无限大，所以这是没有边界的情况。

这个情况是我们有一个替入变量，但是找不到一个替出变量导致的，这时候就是无界的情况了，写算法的时候注意判断一下即可。

 

单纯形算法的具体实现

说了那么多，代码怎么写呢？

看一下最开始的线性规划的问题（已经是松弛形式）：

mins.t.−x1−14x2–6x3x1+x2+x3+x4x1+x5x3++x63x2+x3+x7x1,x2,x3,x4,x5,x6,x7====≥04236

我们可以得到下面的矩阵：

C=(−1−14−60000)B=⎛⎝⎜⎜⎜4236⎞⎠⎟⎟⎟A=⎛⎝⎜⎜⎜1100100310111000010000100001⎞⎠⎟⎟⎟

• 矩阵A：就是约束条件的系数（等号左边的系数）
• 矩阵B：就是约束条件的值（等号右边）
• 矩阵C：目标函数的系数值

我们将其拼接起来：

S1=⎛⎝⎜⎜⎜⎜⎜⎜04236−11100−141003−6101101000001000001000001⎞⎠⎟⎟⎟⎟⎟⎟

左下角为B，右上角为C，右下角为A，那么左上角呢？我们放的是-z，初始时-z = 0！

将上面那个矩阵和写成 基本变量 = 非基本变量的形式对比：

z=−x1−14x2–6x3x4=4−x1–x2−x3x5=2–x1x6=3–x3x7=6–3x2–x3

我们发现，对于B、C就是一样的，而A取决于基本变量和非基本变量，非基本变量符号相反，基本变量符号相同。

接着以最开始的线性规划求解过程的第二步为例，来看看我们的矩阵是如何进行运算的，第二步我们的结果如下（我们选择了x1为替入变量，x5为替出变量）：

z=−2−14x2–6x3+x5x4=2–x2−x3+x5x1=2–x5x6=3–x3x7=6–3x2–x3

首先看看约束条件的式子，x1 = 2 – x5 我们改写成： 2 = x1 + x5 , 因此这行矩阵就是： (b,a1,a2…..a7) = (2,1,0,0,0,1,0,0)，其它的类推，注意-z，因此我们的矩阵应该是如下形式的：

S2=⎛⎝⎜⎜⎜⎜⎜⎜2223600100−141003−61011010001−11000001000001⎞⎠⎟⎟⎟⎟⎟⎟

OK，那么S1 如何变成S2的？

首先是第2行，我们是将 x1用x5表示(x1= x5 )，在等式的变换中，就是移项，然后每一个都除以x1的系数。其实用矩阵很简单，这里就是mat[2] /= mat[2][1] ，表示矩阵第二行都除以第二行第一个元素

其它行呢？只要有x1的，我们都用x1 = 2 – x5 来表示，就是其它行的x1的系数 * mat[2]，然后相减，mat[i]= mat[i] – mat[2] * mat[i][1] ,这样就实现了约束条件中替入和替出变量的替换！比如第一行，就是mat[1] = mat[1] – mat[2] * 1变成两行直接相减

现在来看目标函数，对于目标函数，我们也是将x1用 2 – x5来表示，参照上面的思路，同样的减法：mat[0] = mat[0] – mat[2] * -1 = mat[0] + mat[2] 。注意到我们的其实我们的z = -2，而左上角的为 2，也就是-z，这就是我们为啥说左上角是-z的原因。

用矩阵的形式来表示后，可以写出simplex beta0.99代码（去除版权信息、空行等，只需要21行！）：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

# -*- coding: utf-8 -*- # @Date    : 2016/11/17 # @Author  : hrwhisper   import numpy as np   class Simplex ( object ) :      def __init__ ( self , obj , max_mode = False ) :          self . max_mode = max_mode    # default is solve min LP, if want to solve max lp,should * -1          self . mat = np . array ( [ [ 0 ] + obj ] ) * ( - 1 if max_mode else 1 )        def add_constraint ( self , a , b ) :          self . mat = np . vstack ( [ self . mat , [ b ] + a ] )        def solve ( self ) :          m , n = self . mat . shape    # m - 1 is the number slack variables we should add          temp , B = np . vstack ( [ np . zeros ( ( 1 , m - 1 ) ) , np . eye ( m - 1 ) ] ) , list ( range ( n - 1 , n + m - 1 ) )    # add diagonal array          mat = self . mat = np . hstack ( [ self . mat , temp ] )    # combine them!          while mat [ 0 , 1 : ] . min ( ) < 0 :              col = np . where ( mat [ 0 , 1 : ] < 0 ) [ 0 ] [ 0 ] + 1    # use Bland's method to avoid degeneracy. use mat[0].argmin() ok?              row = np . array ( [ mat [ i ] [ 0 ] / mat [ i ] [ col ] if mat [ i ] [ col ] > 0 else 0x7fffffff for i in                              range ( 1 , mat . shape [ 0 ] ) ] ) . argmin ( ) + 1    # find the theta index              if mat [ row ] [ col ] <= 0 : return None    # the theta is ∞, the problem is unbounded              mat [ row ] /= mat [ row ] [ col ]              ids = np . arange ( mat . shape [ 0 ] ) != row              mat [ ids ] -= mat [ row ] * mat [ ids , col : col + 1 ]    # for each i!= row do: mat[i]= mat[i] - mat[row] * mat[i][col]              B [ row ] = col          return mat [ 0 ] [ 0 ] * ( 1 if self . max_mode else - 1 ) , { B [ i ] : mat [ i , 0 ] for i in range ( 1 , m ) if B [ i ] < n }

一个调用的例子：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

"""        minimize -x1 - 14x2 - 6x3        st         x1 + x2 + x3 <=4         x1 <= 2         x3 <= 3         3x2 + x3 <= 6         x1 ,x2 ,x3 >= 0        answer :-32     """ t = Simplex ( [ - 1 , - 14 , - 6 ] ) t . add_constraint ( [ 1 , 1 , 1 ] , 4 ) t . add_constraint ( [ 1 , 0 , 0 ] , 2 ) t . add_constraint ( [ 0 , 0 , 1 ] , 3 ) t . add_constraint ( [ 0 , 3 , 1 ] , 6 ) print ( t . solve ( ) ) print ( t . mat )

首先初始化目标函数，然后不断的使用add_constraint添加约束条件。

注意在上面的Simplex类中，我们在初始化中加入了参数max_mode，处理最大值的情况。

然后在16~18行中，我们初始化了最开始的基本变量为B, 需要松弛的变量有m-1个，合并（m-1） *（ m-1）的一个对角阵和一行有m-1个0的数组（这是目标函数），然后将他们和原来的合并起来，这样就构成了我们的S矩阵。

19行判断是否还有元素可以继续被增大（就是系数为负）

20-22行选择合适的替入和替出变量，若无替出变量，说明原问题无界，我们在23行处理了这种情况。

24~27就是旋转的过程，进行矩阵的行变换。并用B数组记录替入的替入变量。

28行我们返回目标值z，若为最小值，则要*-1，最大值则不用（因为一开始已经*-1了）。然后最后对应x的解就是基本变量为对应的bi，非基本变量为0，注意删除我们松弛添加的变量（所以只要判断下标是否 < n）

simplex 0.99 beta 就是这么少的代码这么容易的就实现了！

来，跟我一起喊：python 大法好！

 

初始解 ≠ 基本可行解以及无解的情况

在你高呼python大法好的时候，！

但是我把它称为beta 0.99版本肯定是有原因的，绝大多数情况下，初始解就是基本可行解，但是也有例外啊！

而且还有无解的情况。(╯‵□′)╯︵┻━┻

栗子

栗子1

栗子1登场：

mins.t.x1+2x2x1+x2x1+x2x1,x2≤2≥1≥0

首先转化为标准形式（>= 改成 <=, *-1），然后再转化为松弛形式：

mins.t.x1+2x2x3=2–x1–x2x4=−1+x1+x2x1,x2,x3,x4≥0

而我们假设的非基本变量全为0，于是有：(x1,x2,x3,x4) = (0,0,2,-1)，但是x4 = -1是不满足条件的。即初始解不是基本可行解。

栗子2

再比如下面的例子（栗子2）：

mins.t.x1+2x2x1+x2x1+x2x1,x2≥2≤1≥0

 

其实这个例子就是例子1改变了个符号而已，但是要>=2，然后又要<=1的情况，这个例子显然是无解的。

我们来看看初始解的情况，继续转化为标准形式，然后再转化为松弛形式：

mins.t.x1+2x2x3=−2+x1+x2x4=1–x1–x2x1,x2,x3,x4≥0

同样的，非基本变量全为0，于是有：(x1,x2,x3,x4) = (0,0,-2,1)，但是x3 = -2是不满足条件的。即初始解不是基本可行解。

simplex beta0.99测试

在上面的两个例子中，用我们的simplex beta0.99跑有啥结果呢？

第1个栗子,第一个矩阵为初始的矩阵，接下来是结果和对应的x1,x2值，然后是最后的矩阵

[[ 0. 1. 2. 0. 0.]

[-1. -1. -1. 1. 0.]

[ 2. 1. 1. 0. 1.]]

(-0.0, {})

[[ 0. 1. 2. 0. 0.]

[-1. -1. -1. 1. 0.]

[ 2. 1. 1. 0. 1.]]

可以看到，由于c >=0，直接不迭代了，而这个问题用GLPK计算，正确的结果应该为：z = 1, x1 = 1

第2个栗子：格式同上，结果如下

[[ 0. 1. 2. 0. 0.]

[-2. -1. -1. 1. 0.]

[ 1. 1. 1. 0. 1.]]

(-0.0, {})

[[ 0. 1. 2. 0. 0.]

[-2. -1. -1. 1. 0.]

[ 1. 1. 1. 0. 1.]]

这个应该是无解的。

初始化

从上面的例子中，simplex beta 0.99 可以说是错误的! simplex beta 0.99产生错误的原因就是总把初始解当作基本可行解！

拍拍，打脸(￣ε(#￣)

那么如何做才是正确的呢？

问题回到我们的单纯形算法的第一步：找到一个初始的基本可行解。如何找？

我们首先思考上面的问题为什么会不可行。原因就是因为有bi < 0!

因此，对于一个线性规划问题，有如下的情况：

• 若所有的bi >=0 ，说明初始的基本解就是基本可行解，在这种情况下，simplex beta 0.99是正确的。
• 若有bi < 0, 我们需要进行初始化操作，判断其是否有解（如栗子2），并返回一个基本可行解，然后运行simplex beta 0.99

第一种情况就是之前讨论的，这里讨论第二种情况。

以第一个栗子为例，构造辅助线性规划（auxiliary linear program）如下：

mins.t.x0x1+x2–x0−x1–x2–x0x1,x2,x0≤≤≥02−1

然后求解这个辅助线性规划Laux，如果Laux的最优解x0为0的话，说明这个原线性方程组有解。

下面是算法导论的证明，它证明的是最大化 x0 和我们最小化x0是一样的。  

把Laux 写成松弛形式：

z=x0x3=2–x1–x2+x0x4=−1+x1+x2+x0x1,x2,x3,x4,x0≥0

注意到这个初始解（x1,x2,x3,x4,x0） = (0,0,2,-1,0) 也不是基本可行解。现在马上就可以看到引入x0的原因了，我们把x0做为替入变量，选一个b最小的那一行的基本变量作为替出变量（这里是x4），进行一次旋转操作，得：

z=1–x1–x2+x4x3=2–x1–x2+x0x0=1–x1–x2+x4

进行旋转之后，初始解（x1,x2,x3,x4,x0） 变为 (0,0,2,0,1)，这就是因为x0 的替入 ，使得所有的b >=0

有人可能会问，上面的例子中，只有一个负的，多个负的怎么办？还能保证么？

答案是可以的，因为我们选择替出的是bi 为负的最小的那一行的基本变量，而一开始，我们构建辅助函数时，x0的系数为-1，因此，旋转的时候，矩阵运算相当于其它每一行减去这一行，而b为负，负负得正，必然最后所有的b都>=0。

现在，我们已经有一个基本可行解了，我们求解这个辅助线性规划即可。

和上面的思想一样，这里要么增大x1, 要么增大x2，假设选择x1，然后第二个等式有最严格的限制，选择x0为替出变量，得 x1 = 1 – x2 + x4 – x0

z=x0x3=1–x4+2x0x1=1–x2+x4–x0

此时，基本解为：（x1,x2,x3,x4,x0）= (1,0,1,0,0), 此时z = x0 = 0,无法继续增大某个变量使得z继续减少，因此此时为最优解，就是z =0，说明原问题有解。

接下来，我们要恢复原问题的目标函数，就是用现在的基本变量替代原目标函数中的基本变量（若x0是基本变量，那就要旋转去掉它），此外由于x0 = 0,因此可以将其去掉：

z===x1+2x21+x2+x4–x01+x2+x4

其它的约束条件同理去掉x0可得：

z=1+x2+x4x3=1–x4x1=1–x2+x4

因此，现在，我们通过构造了一个辅助线性规划Laux 将原来的问题转化为上面的线性规划，并且它的初始解就是基本可行解：(x1,x2,x3,x4) = (1,0,1,0)，然后求解这个新的线性规划即可。

我们很幸运的发现（其实是博主偷懒举了个简单的例子(✿◡‿◡)），这里无法通过增大任何的变量使得目标值变小，因此此时就是结果啦，而(x1,x2,x3,x4) = (1,0,1,0) 就是最后的解，z = 1。

下面总结一下上面的过程，

1. 若bi都大于等于0 跳到9
2. 引入x0，创建一个辅助线性规划 Laux
3. 将Laux写成松弛形式
4. 选择bi最小的那一行的基本变量为替出变量，x0为替入变量，进行一次旋转操作
5. 求解Laux
6. 若Laux的最优解为0，那么原问题有解，否则无解，return “no answer”
7. 在有解的情况下，若x0为基本解，那么执行一次旋转，把它变为非基本变量
8. 恢复原始的目标函数，但是将其基本变量替换掉
9. 运行simplex beta 0.99 对新的线性规划方程求解。

PS：有兴趣的读者可以计算一下例子2，会发现辅助函数的最优解不是0,而是0.5，说明无解

 

完整的单纯形算法

结合simplex beta 0.99和初始化的过程，可以写成如下的simplex 1.0代码（去除版权信息，空行等，也只要40行左右，还是简洁^ ^）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

# -*- coding: utf-8 -*- # @Date    : 2016/11/17 # @Author  : hrwhisper   import numpy as np   class Simplex ( object ) :      def __init__ ( self , obj , max_mode = False ) :    # default is solve min LP, if want to solve max lp,should * -1          self . mat , self . max_mode = np . array ( [ [ 0 ] + obj ] ) * ( - 1 if max_mode else 1 ) , max_mode        def add_constraint ( self , a , b ) :          self . mat = np . vstack ( [ self . mat , [ b ] + a ] )        def _simplex ( self , mat , B , m , n ) :          while mat [ 0 , 1 : ] . min ( ) < 0 :              col = np . where ( mat [ 0 , 1 : ] < 0 ) [ 0 ] [ 0 ] + 1    # use Bland's method to avoid degeneracy. use mat[0].argmin() ok?              row = np . array ( [ mat [ i ] [ 0 ] / mat [ i ] [ col ] if mat [ i ] [ col ] > 0 else 0x7fffffff for i in                              range ( 1 , mat . shape [ 0 ] ) ] ) . argmin ( ) + 1    # find the theta index              if mat [ row ] [ col ] <= 0 : return None    # the theta is ∞, the problem is unbounded              self . _pivot ( mat , B , row , col )          return mat [ 0 ] [ 0 ] * ( 1 if self . max_mode else - 1 ) , { B [ i ] : mat [ i , 0 ] for i in range ( 1 , m ) if B [ i ] < n }        def _pivot ( self , mat , B , row , col ) :          mat [ row ] /= mat [ row ] [ col ]          ids = np . arange ( mat . shape [ 0 ] ) != row          mat [ ids ] -= mat [ row ] * mat [ ids , col : col + 1 ]    # for each i!= row do: mat[i]= mat[i] - mat[row] * mat[i][col]          B [ row ] = col        def solve ( self ) :          m , n = self . mat . shape    # m - 1 is the number slack variables we should add          temp , B = np . vstack ( [ np . zeros ( ( 1 , m - 1 ) ) , np . eye ( m - 1 ) ] ) , list ( range ( n - 1 , n + m - 1 ) )    # add diagonal array          mat = self . mat = np . hstack ( [ self . mat , temp ] )    # combine them!          if mat [ 1 : , 0 ] . min ( ) < 0 :    # is the initial basic solution feasible?              row = mat [ 1 : , 0 ] . argmin ( ) + 1    # find the index of min b              temp , mat [ 0 ] = np . copy ( mat [ 0 ] ) , 0    # set first row value to zero, and store the previous value              mat = np . hstack ( [ mat , np . array ( [ 1 ] + [ - 1 ] * ( m - 1 ) ) . reshape ( ( - 1 , 1 ) ) ] )              self . _pivot ( mat , B , row , mat . shape [ 1 ] - 1 )              if self . _simplex ( mat , B , m , n ) [ 0 ] != 0 : return None    # the problem has no answer                if mat . shape [ 1 ] - 1 in B :    # if the x0 in B, we should pivot it.                  self . _pivot ( mat , B , B . index ( mat . shape [ 1 ] - 1 ) , np . where ( mat [ 0 , 1 : ] != 0 ) [ 0 ] [ 0 ] + 1 )              self . mat = np . vstack ( [ temp , mat [ 1 : , : - 1 ] ] )    # recover the first line              for i , x in enumerate ( B [ 1 : ] ) :                  self . mat [ 0 ] -= self . mat [ 0 , x ] * self . mat [ i + 1 ]          return self . _simplex ( self . mat , B , m , n )

上面的代码中，将旋转操作独立为一个方法（23~27），将单纯形算法的核心也独立为一个方法（14~21），这是考虑到要多次调用的原因，并且代码之前的几乎没什么变化，这里不做过多的解释。

主要变化在于solve方法，30~32和之前是一样的，不解释 ♪(^ ∇^*)

33行判断是否有一个b < 0 ？如果有，说明初始解不可行。否则直接执行45行，调用单纯形算法

34~44处理的是不可行的情况，

• 34：首先找一个最小b的下标
• 35和36作用在于保存原来的目标函数，并将第0行设为0，然后添加x0 需要拼接矩阵，其实就是构造辅助线性规划Laux
• 37执行旋转操作，使其初始解可行
• 38行求解Laux 最优值是否为0，是就是有解，否则无解
• 40-41行若最后的x0是基本解，找一个第0行不是0的元素作为替入变量，将x0替出
• 42~44 恢复初始目标函数，删除x0那一列，并且替换目标函数中的基本变量。

好了，代码还是很短，其实能更短，但是会影响可读性！

再来高呼： Python 大法好！

 

从几何角度看单纯形算法

上面我们介绍单纯形算法的时候，是通过最直观的等式变换（就是旋转操作）介绍的。

我们知道，线性规划就是在可行域围成的多胞形中求解，现在从几何的视图来看看单纯形算法。

 

只需考虑顶点

让我再次召唤之前的图：

直观上看，最优解就在顶点上，不需要考虑内部点。

一个引入的证明

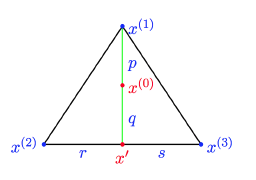
我们假设x(0) 是最优解，连接x(1)和x(0) 与 x(2)和x(3)相交于点x’

我们可以把x(0) 分解，x(0) = λ1 x(1) + (1 – λ1)x’ 其中λ1 = p / (p + q)

同样的把x‘ 分解，x’ = λ2 x(2) + (1 – λ2)x(3) 其中λ2 = r / (r + s)

因此有：x(0) = λ1 x(1) + (1 – λ1)λ2 x(2) + (1 – λ1) (1 – λ2)x(3)，而λ1 + (1 – λ1)λ2 + (1 – λ1) (1 – λ2) = 1

设 cT x(1) 小于等于 cT x(2)， cT x(3)，因此有：

CTx(0)=λ1CTx(1)+(1–λ1)λ2CTx(2)+(1–λ1)(1–λ2)CTx(3)≥λ1CTx(1)+(1–λ1)λ2CTx(1)+(1–λ1)(1–λ2)CTx(1)=CTx(1)

因此，x(1) 并不比x(0) 差。

我们可以推广到更多的情况。(见附件的68页)

 

多边形的顶点等价于矩阵的基

上面提到，最优解一定在顶点上，我们不需要考虑内部的点。

那么，如何获得顶点呢？

可以证明，顶点就是基，基就是顶点。（见附件的72-78页）

我们只需要找到矩阵的基就好了。

 

顶点的游走

我们知道，多边形的顶点就是基，且最优解在顶点上，我们需要做的就是，按照一定的规则沿着边遍历顶点，直到不能更新了为止。

如何从一个顶点到另一个顶点？更新到什么时候为止？

我们先讨论第一个问题。

还是一开始介绍单纯形算法的例子：

mins.t.−