kitti数据集在3D目标检测中的入门(二)可视化详解

推荐阅读第一篇博客：https://blog.csdn.net/qq_37534947/article/details/106628308
因为在写第一篇的时候对于kitti数据集的用法总结的不是太清楚，这里根据可视化代码，然后重新总结一下其主要的流程认知：
一：点云数据bin投影到图像上
一个bin文件对应一个360°方向的点云:

可以看到其中间黑的位置是车所在的位置，以中心点的3D坐标下，一个bin文件存储着多个点的坐标，(x,y,z,r)，r表示反射的强度这里一般用不到。

pointcloud = np.fromfile(str("G:/3Ddet/Point-GNN/000000.bin"), dtype=np.float32, count=-1).reshape([-1, 4])

print(pointcloud.shape)
x = pointcloud[:, 0]  # x position of point
y = pointcloud[:, 1]  # y position of point
z = pointcloud[:, 2]  # z position of point
r = pointcloud[:, 3]  # reflectance value of point
d = np.sqrt(x ** 2 + y ** 2)  # Map Distance from sensor

可以通过以上代码，得到每个点的x，y，z的值，一个bin文件大约有10万多个点。

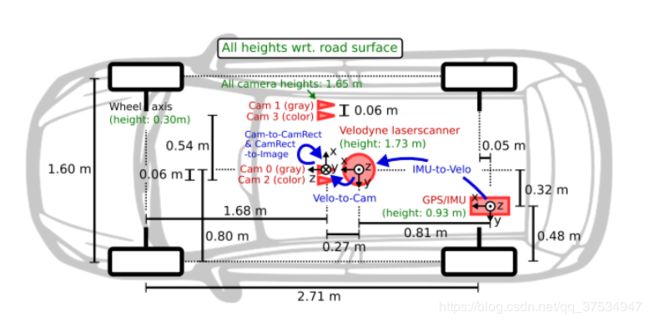
（1）将点云下的坐标系转换到以0号照相机下的坐标系下，需要利用到外参矩阵。
其过程：
1.1：假设n个点，则得到矩阵nx3：

1.2：然后齐次矩阵利用1扩充成nx4大小：

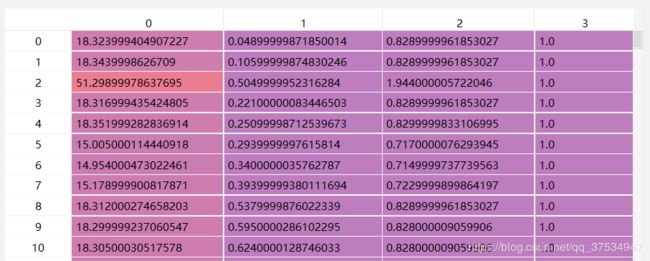
1.3：然后点乘外参矩阵 np.dot(pts_3d_velo, np.transpose(self.V2C))，其中V2C是34列，格式为：

旋转矩阵是坐标系的转换，平移矩阵是坐标原点的移动，从给出的标注文件看出bin文件对应的矩阵有的是不同，这里我认为是因为每天的拍摄的震动会导致稍微有一点不同，但是平移中的0.27m（z轴方向，见上面的车图）大致是不变的。得到结果nx3，即每个点在相机坐标系下的坐标：

1.4：之后利用0号相机的修正矩阵进行修正：
R0修正矩阵3x3：
np.transpose(np.dot(self.R0, np.transpose(pts_3d_ref)))，得到nx3：

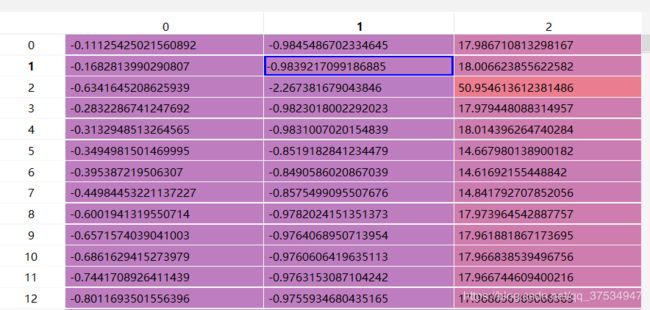
这里为什么修正？主要是随着时间的偏移，0号相机的坐标可能会有偏差，将其校准，然后后面的投影即可通过内参矩阵和位移完成。
1.5：之后齐次矩阵填充1得到nx4，为了后面的运算：

1.6：pts_2d = np.dot(pts_3d_rect, np.transpose(self.P)) 进行内参矩阵的点乘，然后投影到图像上：

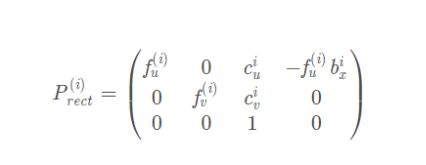
内参矩阵只和相机的内部参数有关：焦距f和光心位置c，每个相机的焦距是一样的。
这里首先需要注意的是：图像的像素坐标系原点在左上角，而上面公式假定原点在图像中心，为了处理这一偏移，设光心在图像上对应的像素坐标为(cu,cv)，所以需要填上cu和cv—cx，cy。

其中的45.7=0.06f=0.06*707=45，上面的最后一列是相机坐标系的偏移，主要是x轴**，y和z轴稍微有点误差**。
得到：

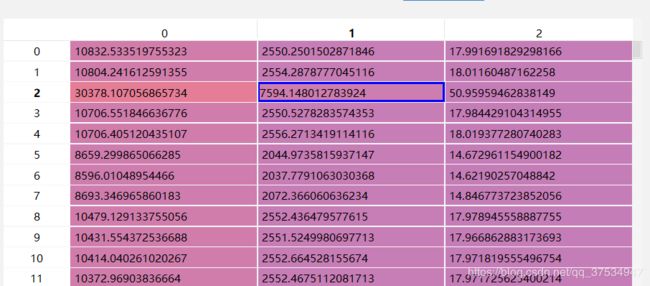
因为内参矩阵的类似于：

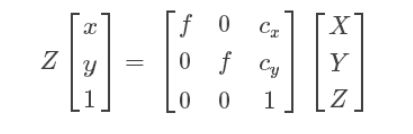
所以要得到图片上的x，y需要pts_2d[:, 0] /= pts_2d[:, 2]； pts_2d[:, 1] /= pts_2d[:, 2]，最后结果为：

最后每个点转换的坐标就完成了。
这里需要注意的几点是：在修正矩阵的时候以及在内参矩阵相乘的时候的有一些小的误差值的相乘，可能主要是由于摄像机的位置变化导致，主要计算细节处，涉及到了内参矩阵和外参矩阵以及图像校正的问题，可以着重看看这个，这里对于其中的细节处不是太深的了解，因为主要参数都已经提供了，所以按其公式直接用即可，而图片主要是为了显示方便而已，一般只利用到点云的话，基本不用考虑这个。
二：将0号照相机3D标注框转换到点云下的坐标系。
0号相机下坐标系的标注：x,y,z,l,w,h，主要提取8个顶点，然后分别转换到点云坐标系下，即作为点云的gt。
其主要步骤为：
2.1： R = roty(obj.ry)，得到标注文件的第15个参数，角度ry：
3D物体的空间方向（rotation_y）取值范围为：-pi ~ pi（单位：rad），它表示，在照相机坐标系下，物体的全局方向角（物体前进方向与相机坐标系x轴的夹角）

R设置为:
[ [cost 0 sint]
[0 1 0]
[sint 0 -cost] ],
其中我看可视化代码写的是
[ [cost 0 sint]
[0 1 0]
[-sint 0 cost] ]，
但是推导后感觉其是错误的，但是现实的结果竟然是一样的，所以需要待考证。

2.2通过角度得到8个点的坐标：

	R = roty(obj.ry)
	# 3d bounding box dimensions
    l = obj.l
    w = obj.w
    h = obj.h

    # 3d bounding box corners
    x_corners = [l / 2, l / 2, -l / 2, -l / 2, l / 2, l / 2, -l / 2, -l / 2]
    y_corners = [0, 0, 0, 0, -h, -h, -h, -h]
    z_corners = [w / 2, -w / 2, -w / 2, w / 2, w / 2, -w / 2, -w / 2, w / 2]

    # rotate and translate 3d bounding box
    corners_3d = np.dot(R, np.vstack([x_corners, y_corners, z_corners]))
    # print corners_3d.shape
    #得到8个点的坐标（x，y，z） 位置是底部（右前，右后，左前，左后） 顶部----
    corners_3d[0, :] = corners_3d[0, :] + obj.t[0]
    corners_3d[1, :] = corners_3d[1, :] + obj.t[1]
    corners_3d[2, :] = corners_3d[2, :] + obj.t[2]

结果为：
#得到8个点的坐标（x，y，z） 位置是底部（右前，右后，左前，左后） 顶部----

其中如何推导来的，主要是利用了相似三角形，可以自己在纸上画一画，不需要考虑此时的y轴，这里假设地面已经是平的了，然后从这里可以看到，（x，y，z）是底部中心点的坐标。
2.3：反矫正，因为（x，y，z）是在矫正后的坐标，所以需要反矫正：
np.transpose(np.dot(np.linalg.inv(self.R0), np.transpose(pts_3d_rect)))
R0见上面，得到：

2.4：齐次式填充1

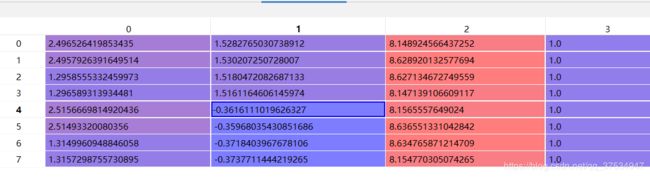
2.5：利用C2V矩阵投影到点云坐标系，np.dot(pts_3d_ref, np.transpose(self.C2V))，其中C2V是由V2C转换而来：

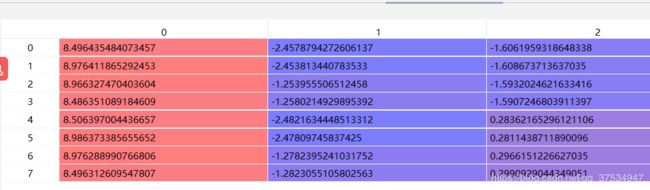
2.6：后面就是画图了
注：以上解释是针对https://github.com/kuixu/kitti_object_vis代码写的。

参考链接：
https://blog.csdn.net/qq_37534947/article/details/106628308