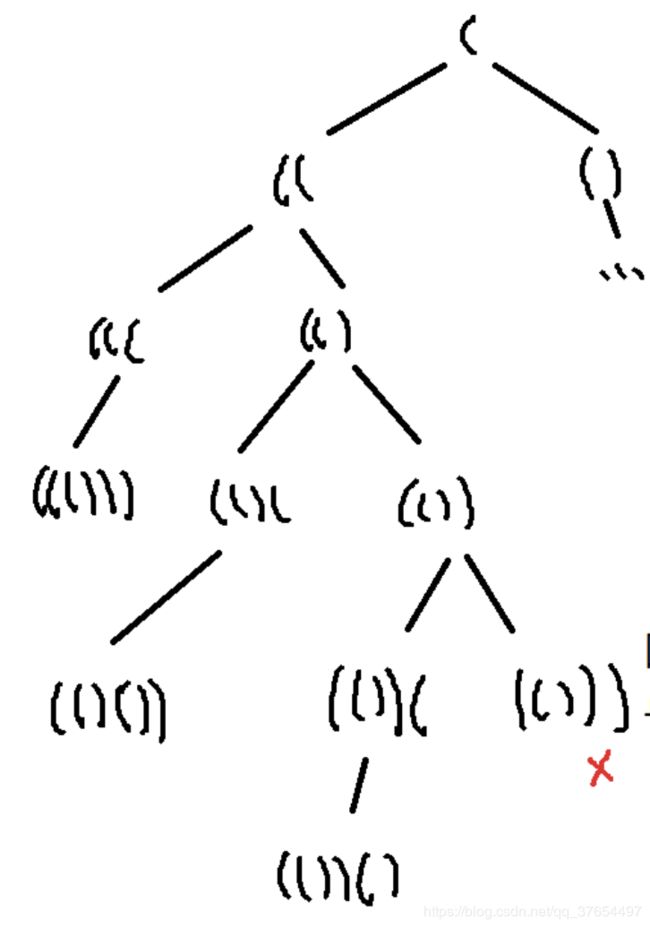常见算法复习整理1
数据结构笔记
1.迭代与递归
递归过程中的递归因子本身可以被忽略(被计入它自己的过程中了)
递归跟踪、递推方程。递归基
减而治之:Decrease and Conquer 线性递归的模式 T(n) = T(n-1)+ O(1)
分而治之:Divide and Conquer 一般出现log(n)都是要用分治法。
这两个都是分治法。
动态规划算法与分治法最大的差别是:适合于用动态规划法求解的问题,经分解后得到的子问题往往不是互相独立的(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)(https://www.cnblogs.com/xsyfl/p/6926269.html)
计算复杂度:递推方程
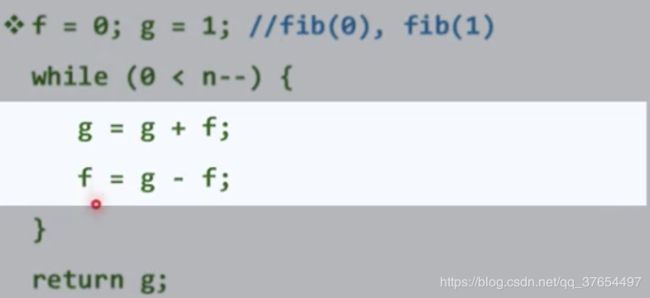
解决递归爆炸(斐波那契数列):递归—>迭代(自底而上)
解决方法A (记忆: memoization ):将已计算过实例的结果制表备查
解决方法B (动态规划: dynamic programming ) 颠倒计算方向:由自顶而下递归,为自底而上迭代
实例1:斐波那契数列
实例2:最长子序列LCS
https://blog.csdn.net/huanghanqian/article/details/78892808
(完成lcs
2.回溯法
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
回溯法中函数的参数一般很有特点,终止条件通常与某个参数有关,一般还有一个参数代表一个子问题的解的形成过程,如22题的str,17题的s,39题的single。。
实例1:leetcode-22-生成括号
注意终止条件为右括号数==n
public List generateParenthesis(int n) {
List res = new ArrayList();
back("",res,0,0,n);
return res;
}
public void back(String str,List list,int l,int r,int n){
if(r==n)////因为right是右括号,数量=n 表明此时已经找到一个结果
list.add(str);
if(l 实例2:leetcode-17-电话号码的字母组合
class Solution {
String[] ss = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
List res = new ArrayList<>();
public List letterCombinations(String digits) {
if(digits.length()==0)
return res;
back("",digits,0);
return res;
}
public void back(String s,String digits,int index){
if(index==digits.length()){
res.add(s);
return;
}
String temp = ss[(digits.charAt(index)-'0')];
for(int i = 0;i 实例3:leetcode-39-组合总和
class Solution {
//类似于走楼梯
public List> combinationSum(int[] candidates, int target) {
List> res = new ArrayList>();
List temp = new ArrayList<>();
Arrays.sort(candidates);
cal(res,temp,candidates,target,0);
return res;
}
public void cal(List> all,List single,int[] candidates,int target,int num){
if(target == 0){
all.add(single);
return;
}
if(candidates[num]>target)
return;
for(int i = num;i list=new ArrayList<>(single);
list.add(candidates[i]);
//递归运算,将i传递至下一次运算是为了避免结果重复
cal(all,list,candidates,target-candidates[i],i);
}
}
} 113. 路径总和 II
class Solution {
List> res = new ArrayList<>();
public List> pathSum(TreeNode root, int sum) {
recall(root,new ArrayList(),sum);
return res;
}
public void recall(TreeNode root,List list,int sum){
if(root==null)
return;
sum -=root.val;
list.add(root.val);
if(sum==0&&root.left==null&&root.right==null)
res.add(list);
List tmp = new ArrayList<>(list);
recall(root.left,list,sum);
recall(root.right,tmp,sum);
}
} 3. 动态规划:
https://blog.csdn.net/hearthougan/article/details/53749841
例1:
class Solution {
/*
设n个结点的树能组成bst个数为dp(n),以点i为根结点构成的bst数目为f(i);
根据以上假设,我们可以先得出dp(0) = 0,dp(1) = 1,这是边界条件;
因为bst的个数应该为以每个结点作为根结点能构成的bst数目的总和,则有dp(n) = f(1) + f(2) + f(3) + ... + f(n):$ \sum_{i=0}^{n}f(i) $
再来看下如何计算f(i)的值,每个结点构成的bst树数目实际上应该等于所有左子孙结点构成bst数目与所有右子孙结点构成bst数目的乘积,即f(i) = dp(i-1) * dp(n-i);
所以最后公式就变成了dp(n) = dp(0) * dp(n-1) + dp(1) * dp(n-2) + ... + dp(n-1) * dp(0);即:$ dp(n)=\sum_{i=0}^{n}dp(i-1)*dp(n-i-1)$
*/
//注意纯迭代怎么实现
public int numTrees(int n) {
if(n<3)
return n;
int []dp = new int[n+1];
dp[0]=1;dp[1]=1;dp[2]=2;
for(int i=3;i<=n;i++){//与上面博客里自底向上的方法一样,i代表对规模为i的问题求解
for(int j=0;j先、中、后序遍历,深广度优先搜索:
https://www.cnblogs.com/xiaolovewei/p/7763867.html
图:
栈与队列 图 树(搜索书、b-tree,红黑树) 词典 堆、优先队列 串
AVL树插入删除算法
https://blog.csdn.net/FreeeLinux/article/details/52204851
1:花朵数_蓝桥杯题目
一个N位的十进制正整数,如果它的每个位上的数字的N次方的和等于这个数本身,则称其为花朵数。
例如:
当N=3时,153就满足条件,因为 1^3 + 5^3 + 3^3 = 153,这样的数字也被称为水仙花数(其中,“^”表示乘方,5^3表示5的3次方,也就是立方)。
当N=4时,1634满足条件,因为 1^4 + 6^4 + 3^4 + 4^4 = 1634。
当N=5时,92727满足条件。
实际上,对N的每个取值,可能有多个数字满足条件。
程序的任务是:求N=21时,所有满足条件的花朵数。
题目分析
看到这个题一般第一想法是暴力枚举,经过简单的计算比较,一般电脑cpu的计算速度在10^10次方/s 这个级别,而10^21次方这个级别的运算量显然超过了合理的时间限制,所以简单的暴力枚举不可取,需要对原计算方法进行化简。
经过简单的枚举,发现花朵数的和与花朵数本身数值无关,只取决于它的21位上0~9 这10个数字出现的次数,如153和351、135、531等等的和都是153,而在暴力枚举的时候会把这几个数都计算一遍。从这可以发现算法改进的地方,即用各个数字出现的次数代替暴力枚举,建立一个数组,存储0-9的出现次数,可知数组的元素之和为21(总次数即位数),因此当 前9个数的次数定下来后,最后一个数字的次数也就定下来了。最后判断是否为花朵数,1)计算他们的和是否是21位,不是的直接pass 2)拿上一步的和,统计各个数出现的次数,与之前建立的数组做比较,若每个数字出现的次数都相等,则打印出结果。
代码需要用到大数运算,递归。
public static void flower()
{
BigInteger[] num={Fn(0),Fn(1),Fn(2),Fn(3),Fn(4),Fn(5),Fn(6),Fn(7),Fn(8),Fn(9)};//定义一个数组存贮每个数字的21次方
int [] cishu=new int [10];//定义一个数组存贮每个数字在21位数中出现的次数
fun(num,cishu,0,0);
}
/*
* 求n的21次方
*/
public static BigInteger Fn(int n)
{
BigInteger sum=BigInteger.ONE;
for(int i=0;i<21;i++)
{
sum=sum.multiply(BigInteger.valueOf(n));
}
return sum;
}
//m表示当前处理的是数组cishu的第几位
//n表示21位的名额已经甩掉了多少
public static void fun(BigInteger[] num, int[] cishu, int m, int n)
{
if(m==9)
{
cishu[9]=21-n;
jisuan(num,cishu);
return ;
}
//对当前位置所有可能进行枚举
for(int i=0;i<21-n;i++)
{
cishu[m]=i;
fun(num,cishu,m+1,n+i);
}
}
public static void jisuan(BigInteger[] num, int[] cishu)
{
BigInteger ss=BigInteger.ZERO;
for(int i=0;i<10;i++)
{
ss=ss.add(num[i].multiply(BigInteger.valueOf(cishu[i])));
}
String str=""+ss;
if(str.length()!=21)
{
return ;
}
int [] result=new int [10];
//result内存放和的21位形式
for(int i=0;i<21;i++)
{
result[str.charAt(i)-'0']++;
}
//测试数组cishu和数组result是否完全匹配
for(int i=0;i<10;i++)
{
if(cishu[i]!=result[i])
{
return ;
}
}
//完全匹配,打印结果
System.out.println(str);
}
2:摩尔投票法
提问: 给定一个int型数组,找出该数组中出现次数大于数组长度一半的int值。
解决方案: 遍历该数组,统计每个int值出现次数,再遍历该集合,找出出现次数大于数组长度一半的int值。
同样的,该解决办法也要求使用Map,否则无法达到线性的时间复杂度。
那么对于这个问题,有没有什么不使用Map的线性算法呢?
答案就是摩尔投票法。利用该算法来解决这个问题,我们可以达到线性的时间复杂度以及常量级的空间复杂度。
摩尔投票法的基本思想很简单,在每一轮投票过程中,从数组中找出一对不同的元素,将其从数组中删除。这样不断的删除直到无法再进行投票,如果数组为空,则没有任何元素出现的次数超过该数组长度的一半。如果只存在一种元素,那么这个元素则可能为目标元素。
那么有没有可能出现最后有两种或两种以上元素呢?根据定义,这是不可能的,因为如果出现这种情况,则代表我们可以继续一轮投票。因此,最终只能是剩下零个或一个元素。
在算法执行过程中,我们使用常量空间实时记录一个候选元素c以及其出现次数f(c),c即为当前阶段出现次数超过半数的元素。根据这样的定义,我们也可以将摩尔投票法看作是一种动态规划算法。
程序开始之前,元素c为空,f(c)=0。遍历数组A:
* 如果f(c)为0,表示截至到当前子数组,并没有候选元素。也就是说之前的遍历过程中并没有找到超过半数的元素。那么,如果超过半数的元素c存在,那么c在剩下的子数组中,出现次数也一定超过半数。因此我们可以将原始问题转化为它的子问题。此时c赋值为当前元素, 同时f(c)=1。
* 如果当前元素A[i] == c, 那么f(c) += 1。(没有找到不同元素,只需要把相同元素累计起来)
* 如果当前元素A[i] != c,那么f(c) -= 1 (相当于删除1个c),不对A[i]做任何处理(相当于删除A[i])
如果遍历结束之后,f(c)不为0,则找到可能元素。
再次遍历一遍数组,记录c真正出现的次数,从而验证c是否真的出现了超过半数。上述算法的时间复杂度为O(n),而由于并不需要真的删除数组元素,我们也并不需要额外的空间来保存原始数组,空间复杂度为O(1)。
//leetcode-169
class Solution
{
public int majorityElement(int[] nums)
{
int major = nums[0];
int count = 1;
for (int i = 1; i < nums.length; i++) {
if (major == nums[i]) {
count++;
} else if (--count == 0) {
major = nums[i + 1];
}
}
return major;
}
}
//未针对题优化的版本
public int majorityElement(int[] nums) {
int majority = -1;
int count = 0;
for (int num : nums) {
if (count == 0) {
majority = num;
count++;
} else {
if (majority == num) {
count++;
} else {
count--;
}
}
}
int counter = 0;
if (count <= 0) {
return -1;
} else {
for (int num : nums) {
if (num == majority) counter ++;
}
}
if (counter > nums.length / 2) {
return majority;
}
return -1;
} //leetcode-229
class Solution {
public List majorityElement(int[] nums) {
/**
首先可以明确的一点是,这样的元素可能有0个、1个、或者2个,再没有别的情况了.
然后,求众数I 里的 Boyer-Moore 算法思路在这里依然可用,但需要些改动:
1) 满足条件的元素最多有两个,那么需要两组变量. count, major变成了
count1, major1; count2, major2;
2) 选出的两个元素,需要验证它们的出现次数是否真的满足条件.
**/
List ret = new ArrayList<>();
if(nums.length < 1) return ret;
int count1 = 0, count2 = 0;
int major1 = nums[0], major2 = nums[0];
for(int num : nums) {
if(num == major1)
count1++;
else if(num == major2)
count2++;
else if(count1 == 0) {
count1 = 1;
major1 = num;
}
else if(count2 == 0) {
count2 = 1;
major2 = num;
}
else {
count1--;
count2--;
}
}
count1 = 0;
count2 = 0;
for(int num : nums) {
if(num == major1)
count1++;
else if(num == major2)
count2++;
}
if(count1 > nums.length/3)
ret.add(major1);
if(major1 != major2 && count2 > nums.length/3)
ret.add(major2);
return ret;
}
} 其实这样的算法也可以衍生到其它频率的问题上,比如说,找出所有出现次数大于n/3的元素。同样可以以线性时间复杂度以及常量空间复杂度来实现。
3. 求子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]class Solution {
//位运算法
public List> subsets(int[] nums) {
List> ret = new ArrayList<>();
int len = nums.length;
for(int i = 0;i tmp = new ArrayList<>();
for(int j = 0;j 4.滑窗法
滑动窗方法算是解决数组或者字符串中,处理连续的字符串段应该想到的一种方法,这里面有变长滑动窗,和定长滑动窗。滑动窗问题总共要处理两个方面,一个是新加入点和处理和移除滑动窗点点的处理。
通用伪代码:
https://blog.csdn.net/haolexiao/article/details/54781671
void slidingwindows(vector nums,int k){
先预处理
然后进行滑动窗的循环,一般是个while循环,同时实现定义好滑动窗的起点和终点,同时还有一个是记录当前状态的数或者数组,比如count
int begin = 0, end = 0;
int count = 0;
while(end public int numSubarrayProductLessThanK(int[] nums, int k) {
if(k==0)
return 0;
int res = 0, l = 0,r = 0;
int len = nums.length,mul = 1;
while(r=k){
mul /= nums[l++];
}
res += r - l;////前面是n位,增加一位后,子数组个数增加n+1个
}
return res;
} 滑窗法模版
https://blog.csdn.net/binling/article/details/45747193
5.最大子序和(字符串的一系列问题:如最长回文xx等等
leetcode-53
Kadane算法扫描一次整个数列的所有数值,在每一个扫描点计算以该点数值为结束点的子数列的最大和(正数和)。该子数列由两部分组成:以前一个位置为结束点的最大子数列、该位置的数值。因为该算法用到了“最佳子结构”(以每个位置为终点的最大子数列都是基于其前一位置的最大子数列计算得出),该算法可看成动态规划的一个例子。
class Solution {
//f[n] = max(0, f[n-1]) + num[n]
/*以第n个数为结束点的子数列的最大和,
存在一个递推关系f(n) = max(f(n-1) + A[n], A[n]);
上面的max(0, f[n-1]) + num[n]等效于max(f(n-1) + A[n], A[n])
*/
public int maxSubArray(int[] nums) {
if(nums.length == 0) return 0;
int max = Integer.MIN_VALUE;
int fn = -1;
int len = nums.length;
for(int i = 0;i6.对称二叉树
递归:
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
//把问题变成判断两棵树是否是对称的
return isSym(root.left, root.right);
}
//判断的是根节点为r1和r2的两棵树是否是对称的
public boolean isSym(TreeNode r1, TreeNode r2){
if(r1 == null && r2 == null) return true;
if(r1 == null || r2 == null) return false;
//这两棵树是对称需要满足的条件:
//1.俩根节点相等。 2.树1的左子树和树2的右子树,树2的左子树和树1的右子树都得是对称的
return r1.val == r2.val && isSym(r1.left, r2.right)
&& isSym(r1.right, r2.left);
}
}迭代
public boolean isSymmetric(TreeNode root) {
Queue q = new LinkedList<>();
q.add(root);
q.add(root);
while (!q.isEmpty()) {
TreeNode t1 = q.poll();
TreeNode t2 = q.poll();
if (t1 == null && t2 == null) continue;
if (t1 == null || t2 == null) return false;
if (t1.val != t2.val) return false;
q.add(t1.left);
q.add(t2.right);
q.add(t1.right);
q.add(t2.left);
}
return true;
} 7.最大子序列、最长递增子序列、最长公共子串、最长公共子序列、字符串编辑距离
https://blog.csdn.net/w_s_h_y/article/details/77447901
https://www.cnblogs.com/AndyJee/p/4465696.html
最长上升子序列o(nlogn)复杂度的解法:
https://blog.csdn.net/wqtltm/article/details/81253935#comments
8.KMP算法与BM算法
1)kmp
https://www.cnblogs.com/tangzhengyue/p/4315393.html:
这里我们借鉴数学归纳法的三个步骤(或者说是动态规划):
1、初始状态
2、假设第j位以及第j位之前的我们都填完了
3、推论第j+1位该怎么填
初始状态我们稍后再说,我们这里直接假设第j位以及第j位之前的我们都填完了。也就是说,从上图来看,我们有如下已知条件:
next[j] == k;
next[k] == 绿色色块所在的索引;
next[绿色色块所在的索引] == 黄色色块所在的索引;
这里要做一个说明:图上的色块大小是一样的(好吧,请忽略色块大小,色块只是代表数组中的一位)。
我们来看下面一个图,可以得到更多的信息:
1.由"next[j] == k;"这个条件,我们可以得到A1子串 == A2子串(根据next数组的定义,前后缀那个)。
2.由"next[k] == 绿色色块所在的索引;"这个条件,我们可以得到B1子串 == B2子串。
3.由"next[绿色色块所在的索引] == 黄色色块所在的索引;"这个条件,我们可以得到C1子串 == C2子串。
4.由1和2(A1 == A2,B1 == B2)可以得到B1 == B2 == B3。
5.由2和3(B1 == B2, C1 == C2)可以得到C1 == C2 == C3。
6.B2 == B3可以得到C3 == C4 == C1 == C2
接下来,我们开始用上面得到的条件来推导如果第j+1位失配时,我们应该填写next[j+1]为多少?
next[j+1]即是找strKey从0到j这个子串的最大前后缀:
#:(#:在这里是个标记,后面会用)我们已知A1 == A2,那么A1和A2分别往后增加一个字符后是否还相等呢?我们得分情况讨论:
(1)如果str[k] == str[j],很明显,我们的next[j+1]就直接等于k+1。
用代码来写就是next[++j] = ++k;
(2)如果str[k] != str[j],那么我们只能从已知的,除了A1,A2之外,最长的B1,B3这个前后缀来做文章了。
那么B1和B3分别往后增加一个字符后是否还相等呢?
由于next[k] == 绿色色块所在的索引,我们先让k = next[k],把k挪到绿色色块的位置,这样我们就可以递归调用"#:"标记处的逻辑了。
由于j+1位之前的next数组我们都是假设已经求出来了的,因此,上面这个递归总会结束,从而得到next[j+1]的值。
我们唯一欠缺的就是初始条件了:
next[0] = -1, k = -1, j = 0
另外有个特殊情况是k为-1时,不能继续递归了,此时next[j+1]应该等于0,即把j回退到首位。
即 next[j+1] = 0; 也可以写成next[++j] = ++k;
public static int[] getNext(String ps)
{
char[] strKey = ps.toCharArray();
int[] next = new int[strKey.length];
// 初始条件
int j = 0;
int k = -1;
next[0] = -1;
// 根据已知的前j位推测第j+1位
while (j < strKey.length - 1)
{
if (k == -1 || strKey[j] == strKey[k])
{
next[++j] = ++k;
}
else
{
k = next[k];
}
}
return next;
}现在再看这段代码应该没有任何问题了吧。
优化:
细心的朋友应该发现了,上面有这样一句话:
(1)如果str[k] == str[j],很明显,我们的next[j+1]就直接等于k+1。用代码来写就是next[++j] = ++k;
可是我们知道,第j+1位是失配了的,如果我们回退j后,发现新的j(也就是此时的++k那位)跟回退之前的j也相等的话,必然也是失配。所以还得继续往前回退。
public static int[] getNext(String ps)
{
char[] strKey = ps.toCharArray();
int[] next = new int[strKey.length];
// 初始条件
int j = 0;
int k = -1;
next[0] = -1;
// 根据已知的前j位推测第j+1位
while (j < strKey.length - 1)
{
if (k == -1 || strKey[j] == strKey[k])
{
// 如果str[j + 1] == str[k + 1],回退后仍然失配,所以要继续回退
if (str[j + 1] == str[k + 1])
{
next[++j] = next[++k];
}
else
{
next[++j] = ++k;
}
}
else
{
k = next[k];
}
}
return next;
}kmp算法主程序:
public static int KMP(String ts, String ps) {
char[] t = ts.toCharArray();
char[] p = ps.toCharArray();
int i = 0; // 主串的位置
int j = 0; // 模式串的位置
int[] next = getNext(ps);
while (i < t.length && j < p.length) {
if (j == -1 || t[i] == p[j]) { // 当j为-1时,要移动的是i,当然j也要归0
i++;
j++;
} else {
// i不需要回溯了
// i = i - j + 1;
j = next[j]; // j回到指定位置
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}9.原地算法
使用原地算法,一般就会牵涉到编解码问题。
//https://segmentfault.com/a/1190000003819277
public void gameOfLife(int[][] board) {
int m = board.length, n = board[0].length;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
int lives = 0;
// 判断上边
if(i > 0){
lives += board[i - 1][j] == 1 || board[i - 1][j] == 2 ? 1 : 0;
}
// 判断左边
if(j > 0){
lives += board[i][j - 1] == 1 || board[i][j - 1] == 2 ? 1 : 0;
}
// 判断下边
if(i < m - 1){
lives += board[i + 1][j] == 1 || board[i + 1][j] == 2 ? 1 : 0;
}
// 判断右边
if(j < n - 1){
lives += board[i][j + 1] == 1 || board[i][j + 1] == 2 ? 1 : 0;
}
// 判断左上角
if(i > 0 && j > 0){
lives += board[i - 1][j - 1] == 1 || board[i - 1][j - 1] == 2 ? 1 : 0;
}
//判断右下角
if(i < m - 1 && j < n - 1){
lives += board[i + 1][j + 1] == 1 || board[i + 1][j + 1] == 2 ? 1 : 0;
}
// 判断右上角
if(i > 0 && j < n - 1){
lives += board[i - 1][j + 1] == 1 || board[i - 1][j + 1] == 2 ? 1 : 0;
}
// 判断左下角
if(i < m - 1 && j > 0){
lives += board[i + 1][j - 1] == 1 || board[i + 1][j - 1] == 2 ? 1 : 0;
}
// 根据周边存活数量更新当前点,结果是0和1的情况不用更新
if(board[i][j] == 0 && lives == 3){
board[i][j] = 3;
} else if(board[i][j] == 1){
if(lives < 2 || lives > 3) board[i][j] = 2;
}
}
}
// 解码
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
board[i][j] = board[i][j] % 2;
}
}
}10.染色问题
图的m着色问题
//不能用图有无环去判断,有环也是可以分的,如1->2->3->4->1
//本题类似于经典的染色算法https://blog.csdn.net/qq_38959715/article/details/82191026
private Map> graph886 = new HashMap<>();// 图存放的数据结构
private int[] color886; // 每个节点的颜色
public boolean possibleBipartition(int N, int[][] dislikes) {
if(N<3)
return true;
color886 = new int[N+1];
Arrays.fill(color886,-1);//-1表示未访问,0和1是两种颜色
for(int i = 1;i<=N;i++){
graph886.put(i,new ArrayList<>());
}
for(int [] edge : dislikes){
graph886.get(edge[0]).add(edge[1]);
graph886.get(edge[1]).add(edge[0]);
}
for(int i = 1;i<=N;i++){
if(color886[i]<0){
color886[i] = 0;
if(!possbi_dfs(i))
return false;
}
}
return true;
}
public boolean possbi_dfs(int now){
for(int next : graph886.get(now)){
if(color886[next]<0){
//第一圈为1 第二圈为0 第三圈为1 依次类推(主要是为了判断相邻的两个层会不会染色冲突)
color886[next] = 1 - color886[now];
if(!possbi_dfs(next))
return false;
}else if(color886[next]==color886[now])
return false;
}
return true;
} 11.并查集
https://www.cnblogs.com/xzxl/p/7226557.html
http://www.cnblogs.com/xzxl/p/7341536.html
//并查集
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
int[] pre = new int[n+1];
//每个pre节点初始化为自己
for(int i = 0;i<= n;i++){
pre[i] = i;
}
for(int [] edge : edges){
int root1 = findRoot(edge[0],pre);
int root2 = findRoot(edge[1],pre);
//有共同的根节点,说明在一个连通子图中,此时这条边不能加入,否则会形成环,因此这条边需要删去
if(root1==root2)
return edge;
//并集,将root1下所有子节点的根节点设为root2,方便下次寻找根节点
adjust(edge[0],root2,pre);
}
return new int[0];
}
//寻找该节点的根节点
private int findRoot(int num,int[]pre){
while(pre[num]!=num)
num = pre[num];
return num;
}
//并集 + 路径压缩
private void adjust(int x,int root,int[] pre){
while(pre[x]!=root){
int temp = pre[x];
pre[x] = root;
x = temp;
}
}12.堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
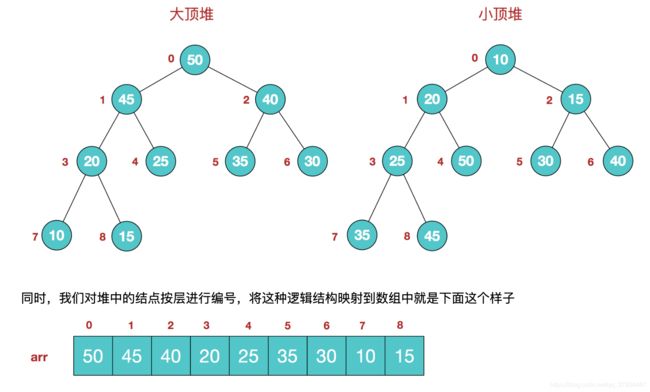
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
代码如下:
public class HeapSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
//1.构建大顶堆
for(int i=arr.length/2-1;i>=0;i--){
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr,i,arr.length);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);//将堆顶元素与末尾元素进行交换
adjustHeap(arr,0,j);//重新对堆进行调整
}
}
//调整大顶堆
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];//先取出当前元素i
for(int k=i*2+1;ktemp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
} 简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
13. 桶排序
14. 线段树
//线段树 也可用前缀和求解 b[i]=b[i-1]+co[i];
//线段树 https://www.cnblogs.com/TheRoadToTheGold/p/6254255.html
//树状数组 https://blog.csdn.net/Small_Orange_glory/article/details/81290634
class NumArray {
private segmentNode root;
private int[] nums;
public NumArray(int[] nums) {
if (nums.length == 0) return ;
this.nums = nums;
root = buildTree(0,nums.length-1);
}
public void update(int i, int val) {
updateNode(root,i,val);
}
public int sumRange(int i, int j) {
return rangeQuery(root,i,j);
}
private int rangeQuery(segmentNode x,int i,int j) {
if (x.start == i && x.end == j) {
return x.sum;
}
int mid = x.start + (x.end - x.start) / 2;
if (j <= mid) return rangeQuery(x.left,i,j);//注意这里的 = 放到i上不行,应该是与mid向下取值有原因
if (i > mid) return rangeQuery(x.right,i,j);
return rangeQuery(x.left,i,mid) + rangeQuery(x.right,mid+1,j);
}
private void updateNode(segmentNode x,int i,int val) {
if (x.start == x.end && x.start == i) {
x.sum = val;
return ;
}
int mid = x.start + (x.end - x.start) / 2;
if (i <= mid) {
updateNode(x.left,i,val);
} else {
updateNode(x.right,i,val);
}
x.sum = x.left.sum + x.right.sum;
return ;
}
private segmentNode buildTree(int start,int end) {
if (start == end) {
return new segmentNode(start,end,nums[start]);
}
int mid = start + (end - start) / 2;
segmentNode node = new segmentNode(start,end,0);
node.left = buildTree(start,mid);
node.right = buildTree(mid+1,end);
node.sum = node.left.sum + node.right.sum;//向上修改,区间修改不适用
return node;
}
class segmentNode {
private int start,end;
private segmentNode left,right;
private int sum;
public segmentNode(int start,int end,int sum) {
this.start = start;
this.end = end;
this.sum = sum;
}
}
}15.最小生成树
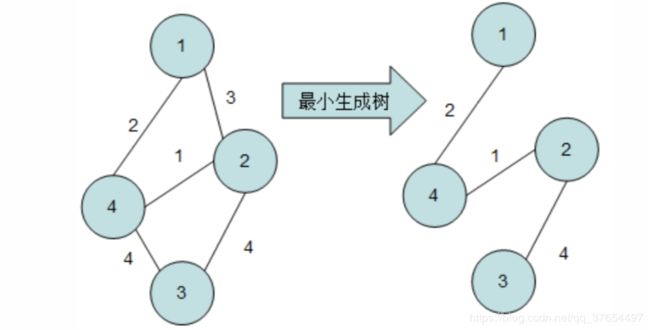
在一个无向连通图中,如果存在一个连通子图包含原图中所有的结点和部分边,且这个子图不存在回路,那么我们称这个子图为原图的一棵生成树。在带权图中,所有的生成树中边权的和最小的那棵(或几棵)被称为最小生成树。
定理:
在要求解的连通图中,任意选择一些点属于集合 A,剩余的点属于集合 B,必定存在一棵最小生成树包含两个顶点分别属于集合 A 和集合 B 的边(即连通 两个集合的边)中权值最小的边。这个结论就是我们将要介绍的求最小生成树 Kruskal 算法的算法原理,它按照按如下步骤求解最小生成树:
1.初始时所有结点属于孤立的集合。
2.按照边权递增顺序遍历所有的边,若遍历到的边两个顶点仍分属不同的集 合(该边即为连通这两个集合的边中权值最小的那条)则确定该边为最小生成树 上的一条边,并将这两个顶点分属的集合合并。
3.遍历完所有边后,原图上所有结点属于同一个集合则被选取的边和原图中 所有结点构成最小生成树;否则原图不连通,最小生成树不存在。
如步骤所示,在用 Kruskal 算法求解最小生成树的过程中涉及到大量的集合 操作,我们恰好可以使用上一节中讨论的并查集来实现这些操作。
1. 邻接矩阵源码
12. 邻接表源码
// 边的结构体
class ENode {
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
public ENode(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
};
// 邻接表中表的顶点
class VNode {
char data; // 顶点信息
ENode firstEdge; // 指向第一条依附该顶点的弧
};
class Graph {
private static final int INF = Integer.MAX_VALUE; // 最大值
char[] vertexs; // 顶点集合
int[][] matrix; // 邻接矩阵
// 得到当前有向图中的所有边信息
public List getEdges() {
List edges = new ArrayList();
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
if (matrix[i][j] != INF) {
ENode edge = new ENode(vertexs[i], vertexs[j], matrix[i][j]);
edges.add(edge);
}
}
}
return edges;
}
}
private static final int INF = Integer.MAX_VALUE; // 最大值
static void qSort(List edges, int low, int high) {
if (low < high) {
int i = low, j = high;
ENode edge = edges.get(low);
while (i < j) {
while (edge.weight < edges.get(j).weight && i < j)
j--;
edges.set(i, edges.get(j));
while (edge.weight > edges.get(i).weight && i < j)
i++;
edges.set(j, edges.get(j));
}
edges.set(i, edge);
qSort(edges, low, i - 1);
qSort(edges, i + 1, high);
}
}
public static void kruskal(Graph G) {
// 1.拿到有向图中所有边
List edges = G.getEdges();
int edgeNum = edges.size();
// 2.对所有有向边进行排序
qSort(edges, 0, edgeNum - 1);
ENode[] minTree = new ENode[G.vertexs.length - 1]; // 结果数组,保存kruskal最小生成树的边
int index = 0; // minTree数组的索引
// 用于保存"已有最小生成树"中每个顶点(以数组下标表示) 与 其经过“最短边”的邻接顶点 (以对应下标的值表示)的并查集
int[] start2end = new int[G.vertexs.length];
// 3.依次将最短且不与T构成回路的边加入T集合
for (int i = 0; i < edgeNum; i++) {
//得到当前最短边 在有向图G中的起始顶点与终结顶点的 下标
int p1 = getIndex(G, edges.get(i).start); // 获取第i条边的"起点"的序号
int p2 = getIndex(G, edges.get(i).end); // 获取第i条边的"终点"的序号
//分别得到在T集合中沿当前最短边的“起点”与“终点”遍历到的最后节点,
//若加入当前最短边后T集合存在回路,则“起点”与“终点”遍历到的最后节点一定是同一节点
int m = getEnd(start2end, p1); // 获取p1在"已有的最小生成树"中的终点
int n = getEnd(start2end, p2); // 获取p2在"已有的最小生成树"中的终点
//当前最短边加入T集合后没有有回路 则将当前最短边加入T集合,并且记录当前最短边的“起点”与“终点”
if (m != n) {
start2end[m] = n; // “起点”即vends的数组下标与“终点”即vends的对应下标的值
minTree[index++] = edges.get(i); // 保存结果
}
}
}
static int getIndex(Graph G, char ch) {
int i = 0;
for (; i < G.vertexs.length; i++)
if (G.vertexs[i] == ch)
return i;
return -1;
}
static int getEnd(int start2end[], int i) {
while (start2end[i] != 0)
i = start2end[i];
return i;
} 16.最小高度树
leetcode310:此问题等同于在无向图中找到一条最长的路径,因为最小高度树的根一定在图的一条最长路径的中点位置,寻找这条最长路径的方法是从任意一点出发,找到最远的点a,然后再从这个最远的点a出发,找到离它最远的点b,a—b即为最长路径。可以用广度优先或者深度优先搜索。
之所以能用这种方法找最长路径,是因为先找到的点a一定是树的叶子节点且处于树中最长或次长的枝上,由此出发找到的b一定是树次长或最长的枝的叶子。
代码如下:
private int maxNode310, maxDepth310;
public List findMinHeightTrees(int n, int[][] edges) {
List roots = new ArrayList<>();
List[] graph = new ArrayList[n];
for(int i=0; i();
for(int i=0; i[] graph, boolean[] visited, int[] prev){
if (depth > maxDepth310) {
maxDepth310 = depth;
maxNode310 = from;
}
for(int next:graph[from]){
if(visited[next]==true)continue;
visited[next] = true;
prev[next] = from;
dfs310(next,depth+1,graph,visited,prev);
}
} 17.矩阵链乘
18.
1)最短路径问题
Floyd 算法
在图的邻接矩阵表示法中,edge[i][j]表示由结点 i 到结点 j 中间 不经过任何结点时的最短距离,那么我们依次为中间允许经过的结点添加结点 1、结点 2、......直到结点 N,当添加完这些结点后,从结点 i 到结点 j 允许经过 所有结点的最短路径长度就可以确定了,该长度即为原图上由结点 i 到结点 j 的 最短路径长度。
我们设 ans[k][i][j]为从结点 i 到结点 j 允许经过编号小于等于 k 的结点时其最短路径长度。如上文,ans[0][i][j]即等于图的邻接矩阵表示中 edge[i][j]的值。我 们通过如下循环,完成所有 k 对应的 ans[k][i][j]值的求解:
for (int k = 1;k <= n;k ++) { //从1至n循环k for (int i = 1;i <= n;i ++) {
for (int j = 1;j <= n;j ++) { //遍历所有的ij
if (ans[k - 1][i][k] == 无穷||ans[k - 1][k][j] == 无穷) { //
若当允许经过前k-1个结点时,i或j不能与k连通,则ij之间到目前为止不存在经过k的路径 ans[k][i][j] = ans[k - 1][i][j]; //保持原值,即从i到j
允许经过前k个点和允许经过前k-1个结点时最短路径长度相同 continue; //继续循环
}
if (ans[k - 1][i][j] == 无穷||ans[k - 1][i][k] + ans[k - 1][k][j] < ans[k - 1][i][j]) //若经过前k-1个结点,i和j不连通 或者 通过经过结点k可
以得到比原来更短的路径 //更新该最短值
}
ans[k][i][j] = ans[k - 1][i][k] + ans[k - 1][k][j]; else ans[k][i][j] = ans[k - 1][i][j]; //否则保持原状
} }经过这样的 n 次循环后,我们即可得到所有结点间允许经过所有结点条件下 的最短路径长度,该路径长度即为我们要求的最短路径长度。即若要求得 ab 之 间的最短路径长度,其答案为 ans[n][a][b]的值。
同时我们注意到,我们在通过 ans[k - 1][i][j]的各值来递推求得 ans[k][i][j]的 值时,所有的 ans[k][i][j]值将由 ans[k - 1][i][j]和 ans[k - 1][i][k] + ans[k - 1][k][j] 的大小关系确定,但同时 ans[k][i][k]和 ans[k][k][j]必定与 ans[k - 1][i][k]和 ans[k - 1][k][j]的值相同,即这些值不会因为本次更新而发生改变。所以我们将如上代码片段简化成如下形式:
for (int k = 1;k <= n;k ++) {
for (int i = 1;i <= n;i ++) {
for (int j = 1;j <= n;j ++) {
if (ans[i][k] == 无穷 || ans[k][j] == 无穷) continue; if(ans[i][j]== 无穷 ||ans[i][k]+ans[k][j]2)单源最短路路径问题
其实在我看来,dijkstra算法和Floyd算法思想一样,不过是在Floyd算法上在针对单个点的最短路径时做了简化。
Dijkstra 算法流程如下:
1.初始化,集合 K 中加入结点 1,结点 1 到结点 1 最短距离为 0,到其它结点为无穷(或不确定)。
2.遍历与集合 K 中结点直接相邻的边(U,V,C),其中 U 属于集合 K,V
不属于集合 K,计算由结点 1 出发按照已经得到的最短路到达 U,再由 U 经过 该边到达 V 时的路径长度。比较所有与集合 K 中结点直接相邻的非集合 K 结点
该路径长度,其中路径长度最小的结点被确定为下一个最短路径确定的结点,其 最短路径长度即为这个路径长度,最后将该结点加入集合 K。
3.若集合 K 中已经包含了所有的点,算法结束;否则重复步骤 2。
//743. 网络延迟时间
//单源最短路径问题
private final int inf1 = 0x3f3f3f3f;
boolean [] visit;
int[] dist;//最短距离
int[][] graph ;
public int networkDelayTime(int[][] times, int N, int K) {
visit = new boolean[N+1];
dist = new int[N+1];
graph = new int[N+1][N+1];
Arrays.fill(dist,inf1);
for(int i=0;i<=N;i++)
for(int j=0;j<=N;j++)
graph[i][j]=i==j?0:inf1;
for(int[] e : times)
graph[e[0]][e[1]] = e[2];
dijkstra(K,N);
int max = 0;
for(int i = 1;imax)
max = dist[i];
}
return max;
}
public void dijkstra(int source ,int N){
dist[source] = 0;
visit[source]=true;
for(int i = 1;idist[index]+graph[index][v])
dist[v]=dist[index]+graph[index][v];
}
}
} 3)dp求解最短路路径问题
用动态规划也可以求出最短路径,时间复杂度为O(n^2),跟没有优化的Dijistra算法一样(优化后的Dijistra算法时间复杂度为O((m+n)lgn))。
![]()
首先这里有15个结点,表现出来的矩阵为:
![]()
左侧1-15表示前一个节点,最上面一行1-15表示后一个节点,记这个图的矩阵为P,那么P[0][1]==5表示节点0与节点1相连,路径长度为5。那么我们如何利用动态规划来求解最短路径?
首先我们需要把整个问题转换成小的子问题,利用小的子问题的最优解求出整个问题的最优解。
我们的目的是求0-15之间的最短路径,由图可知与节点15相连的是结点14和节点13,假设我们已经求出0-13的最短路径的值D13和0-14的最短路径的值D14,那么我们只需要比较D13+d(13-15)和D14+d(14-15)的大小就可以知道从哪个节点出发到节点15的路径最短。按照这个思想一直往前推,推到节点0时结束,自然就求出了节点0-节点15的最短路径,这个思路是递归的,如果用递归的方法,时间复杂度很高,当然你也可以用备忘录,记录已经计算过的值,我这里将递归转换成迭代。
我们先定义一个类class Node,里面存储节点的序号、从0到这个节点的最短路径的值、前一个节点的序号
class node{
public int number;
//value是指从0到这个节点总共要走多远,执行算法前将value的值初始化为无穷大
public int value;
public int parent;
}
//从矩阵a的第一行开始,一行行找相连的节点
for(int i = 0;i<16;i++){
for(int j = 0;j<16;j++){
//找到了相连节点
if(a[i][j]!=0){
//上一个节点的最短路径的值+与下一个节点相连路径上的值
d = n[i].value+a[i][j];
//判断是否比原先的值要小,如果小就将0-j节点的长度替换
if(d最后将n[15].value打印出来就是最短路径的值,再根据parent的值往前找就得到最短路径的解,当然这个例子有不同的路径的解。
leetcode例题:
//787. K 站中转内最便宜的航班 dp 板子题
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
int maxv = Integer.MAX_VALUE;
if(n==1)
return 0;
int[][] dp = new int[n][K+1];
for(int i = 0;i19.字典树
20.LCA 最近公共祖先
Tarjan算法(离线算法)
离线算法,是指首先读入所有的询问(求一次LCA叫做一次询问),然后重新组织查询处理顺序以便得到更高效的处理方法。Tarjan算法是一个常见的用于解决LCA问题的离线算法,它结合了深度优先遍历和并查集,整个算法为线性处理时间。
Tarjan算法是基于并查集的,利用并查集优越的时空复杂度,可以实现LCA问题的O(n+Q)算法,这里Q表示询问 的次数。
同上一个算法一样,Tarjan算法也要用到深度优先搜索,算法大体流程如下:对于新搜索到的一个结点,首先创建由这个结点构成的集合,再对当前结点的每一个子树进行搜索,每搜索完一棵子树,则可确定子树内的LCA询问都已解决。其他的LCA询问的结果必然在这个子树之外,这时把子树所形成的集合与当前结点的集合合并,并将当前结点设为这个集合的祖先。之后继续搜索下一棵子树,直到当前结点的所有子树搜索完。这时把当前结点也设为已被检查过的,同时可以处理有关当前结点的LCA询问,如果有一个从当前结点到结点v的询问,且v已被检查过,则由于进行的是深度优先搜索,当前结点与v的最近公共祖先一定还没有被检查,而这个最近公共祖先的包涵v的子树一定已经搜索过了,那么这个最近公共祖先一定是v所在集合的祖先。
https://www.cnblogs.com/JVxie/p/4854719.html
Tarjan(u)//marge和find为并查集合并函数和查找函数
{
for each(u,v) //访问所有u子节点v
{
Tarjan(v); //继续往下遍历
marge(u,v); //合并v到u上
标记v被访问过;
}
for each(u,e) //访问所有和u有询问关系的e
{
如果e被访问过;
u,e的最近公共祖先为find(e);
}
}#include
#include
#include
#include
#include
#include
#define eps 1e-8
#define memset(a,v) memset(a,v,sizeof(a))
using namespace std;
typedef long long int LL;
const int MAXL(1e4);
const int INF(0x7f7f7f7f);
const int mod(1e9+7);
int dir[4][2]= {{-1,0},{1,0},{0,1},{0,-1}};
int father[MAXL+50];
bool is_root[MAXL+50];
bool vis[MAXL+50];
vectorv[MAXL+50];
int root;
int cx,cy;
int ans;
int Find(int x)
{
if(x!=father[x])
father[x]=Find(father[x]);
return father[x];
}
void Join(int x,int y)
{
int fx=Find(x),fy=Find(y);
if(fx!=fy)
father[fy]=fx;
}
void LCA(int u)
{
for(int i=0; i 按类别刷算法题
一:字符操作类
二:树类
三:动态规划
四:背包问题