NeuralNetworks(BP算法的实现)
***神经网络 (BP算法的实现)***
1.基础知识
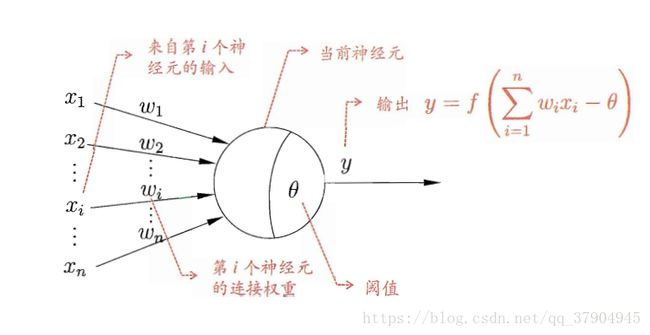
1.1神经元模型
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络
1.2感知机与多层网络
Perceptron 感知机
感知机只有两层神经元组成,而且只有输出层是M-P神经单元也就是功能神经元
1.3 BP算法(error Back Propagation) 误差逆传播算法,也叫反向传播算法
PesudoCode:
输入:训练集
学习率
过程:
1.在(0,1)范围内随机初始化网络中所有的连接权值和阈值
2.repeat
3. for all (Xk,Yk) do
4. 根据当前参数和公式,计算当前样本的输出
5. 根据公式计算出输出层神经元的梯度项
6. 根据公式计算隐层神经元的梯度项
7. 根据公式更新连接权和阈值
8. end for
9. until 达到停止条件
输出:连接权与阈值确定的多层前馈神经网络
注意区分标准BP算法,和累积BP算法(accumulated error backpropagation)
累积BP算法:是将训练集进行读取一遍后才进行更新
标准BP算法:针对一个训练样例进行更新
BP算法容易过拟合,解决过拟合的策略
早停(early stopping):将数据集分为训练集和验证集,训练集用来计算梯度,更新连接权和阈值.
验证集用来估计误当训练集误差减小,但验证集误差升高则停止训练.
正则化(regularization):在目标误差函数增加一个用于描述网络复杂度的部分
1.4 各种模型的介绍
ART网络,SOM网络,结构自适应网络(级连相关网络),Elman网络(recursive neural networks)递归神经网络
Blotzmann机
还有最牛的深度学习(Deep learning)
2.编程实现BP算法,在西瓜数据集3.0上用算法训练一个单隐层神经网络
# input()函数
# 将西瓜数据集3.0进行读取
def input():
"""
@param : none or filepath
@return : dataSet,dataFrame using pandas
Random double or random.uniform()
"""
try:
import pandas as pd
except ImportError:
print("module import error")
with open('/home/dengshuo/GithubCode/ML/CH05/watermelon3.csv') as data_file:
df=pd.read_csv(data_file)
return df# learningRatio()函数
# 初始化函数的学习率
def learningRatio():
"""
@ return : learningRatio
"""
try:
import random
except ImportError:
print('module import error')
learningRatio=random.uniform(0,1)
return learningRatioratio=learningRatio()
print(ratio)
input()
.dataframe thead tr:only-child th { text-align: right; } .dataframe thead th { text-align: left; } .dataframe tbody tr th { vertical-align: top; }
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.697 | 0.460 | 是 |
| 1 | 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 0.774 | 0.376 | 是 |
| 2 | 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.634 | 0.264 | 是 |
| 3 | 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 0.608 | 0.318 | 是 |
| 4 | 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 0.556 | 0.215 | 是 |
| 5 | 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 0.403 | 0.237 | 是 |
| 6 | 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 0.481 | 0.149 | 是 |
| 7 | 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 0.437 | 0.211 | 是 |
| 8 | 9 | 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 0.666 | 0.091 | 否 |
| 9 | 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 0.243 | 0.267 | 否 |
| 10 | 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 0.245 | 0.057 | 否 |
| 11 | 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 0.343 | 0.099 | 否 |
| 12 | 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 0.639 | 0.161 | 否 |
| 13 | 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 0.657 | 0.198 | 否 |
| 14 | 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 0.360 | 0.370 | 否 |
| 15 | 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 0.593 | 0.042 | 否 |
| 16 | 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 0.719 | 0.103 | 否 |
# outputlayer() 函数
# 计算函数输出层的输出值Yk
def outputlayer(df):
"""
@param df: the dataframe of pandas
@return Yk:the output
"""
# 复杂的参数让人头疼# define class()
# define the neural networks structure,创建整个算法的框架
'''
the definition of BP network class
'''
class BP_network:
def __init__(self):
'''
initial variables
'''
# node number each layer
self.i_n = 0
self.h_n = 0
self.o_n = 0
# output value for each layer
self.i_v = []
self.h_v = []
self.o_v = []
# parameters (w, t)
self.ih_w = [] # weight for each link
self.ho_w = []
self.h_t = [] # threshold for each neuron
self.o_t = []
# definition of alternative activation functions and it's derivation
self.fun = {
'Sigmoid': Sigmoid, # 对数几率函数
'SigmoidDerivate': SigmoidDerivate,
'Tanh': Tanh, # 双曲正切函数
'TanhDerivate': TanhDerivate,
}# CreateNN() 函数
# 将架构进行填充
def CreateNN(self, ni, nh, no, actfun):
'''
build a BP network structure and initial parameters
@param ni, nh, no: the neuron number of each layer
@param actfun: string, the name of activation function
'''
# import module packages
import numpy as np
import random
# assignment of node number
# 对每层的结点树的输入值进行赋值
self.i_n = ni
self.h_n = nh
self.o_n = no
# initial value of output for each layer
self.i_v = np.zeros(self.i_n)
self.h_v = np.zeros(self.h_n)
self.o_v = np.zeros(self.o_n)
# initial weights for each link (random initialization)
self.ih_w = np.zeros([self.i_n, self.h_n])
self.ho_w = np.zeros([self.h_n, self.o_n])
# 利用循环来对权值进行赋值
for i in range(self.i_n):
for h in range(self.h_n):
self.ih_w[i][h] = rand(0,1)# float(0,1) # 调用rand()函数
for h in range(self.h_n):
for j in range(self.o_n):
self.ho_w[h][j] = rand(0,1)
# initial threshold for each neuron
self.h_t = np.zeros(self.h_n)
self.o_t = np.zeros(self.o_n)
for h in range(self.h_n): self.h_t[h] = rand(0,1)
for j in range(self.o_n): self.o_t[j] = rand(0,1)
# initial activation function
# 这个不调库能直接用?不是很理解
self.af = self.fun[actfun]
self.afd = self.fun[actfun+'Derivate']
# 随机取值函数的定义
'''
the definition of random function
'''
def rand(a, b):
'''
random value generation for parameter initialization
@param a,b: the upper and lower limitation of the random value
'''
from random import random
return (b - a) * random() + a# define th need functions
# 一些激活函数
'''
the definition of activation functions
'''
def Sigmoid(x):
'''
definition of sigmoid function and it's derivation
'''
from math import exp
return 1.0 / (1.0 + exp(-x))
def SigmoidDerivate(y):
return y * (1 - y)
def Tanh(x):
'''
definition of sigmoid function and it's derivation
'''
from math import tanh
return tanh(x)
def TanhDerivate(y):
return 1 - y*y# predict process through the network
# 计算一个输出
def Pred(self, x):
'''
@param x: the input array for input layer
'''
# activate input layer
for i in range(self.i_n):
self.i_v[i] = x[i]
# activate hidden layer
for h in range(self.h_n):
total = 0.0
for i in range(self.i_n):
total += self.i_v[i] * self.ih_w[i][h]
self.h_v[h] = self.af(total - self.h_t[h])
# activate output layer
for j in range(self.o_n):
total = 0.0
for h in range(self.h_n):
total += self.h_v[h] * self.ho_w[h][j]
self.o_v[j] = self.af(total - self.o_t[j])还有一个问题就是,已经读取的西瓜数据,该以什么样的形式来进行输入
西瓜数据集的离散性变量该如何处理 例如:色泽{青緑,乌黑,浅白}={0,1,2} ??
如何不是这样,怎么实现离散性变量的计算?
# the implementation of BP algorithms on one slide of sample
# backPropagate() 函数
# 后向传播函数,进行计算
def BackPropagate(self, x, y, lr):
'''
@param x, y: array, input and output of the data sample
@param lr: float, the learning rate of gradient decent iteration
'''
# import need module packages
import numpy as np
# get current network output
self.Pred(x)
# calculate the gradient based on output
o_grid = np.zeros(self.o_n)
for j in range(self.o_n):
# 输出层的神经元梯度项,参考西瓜书 5.3 公式(5.10)
o_grid[j] = (y[j] - self.o_v[j]) * self.afd(self.o_v[j])
# 这个self.afd()函数就相当于yk(1-yk)
# caculate the gradient of hidden layer
# 计算隐藏层的梯度项Eh
h_grid = np.zeros(self.h_n)
for h in range(self.h_n):
for j in range(self.o_n):
h_grid[h] += self.ho_w[h][j] * o_grid[j]
h_grid[h] = h_grid[h] * self.afd(self.h_v[h])
# self.afd()函数就是 Bh(1-Bh)
# updating the parameter
# 将参数进行更新
for h in range(self.h_n):
for j in range(self.o_n):
# 更新公式
self.ho_w[h][j] += lr * o_grid[j] * self.h_v[h]
for i in range(self.i_n):
for h in range(self.h_n):
self.ih_w[i][h] += lr * h_grid[h] * self.i_v[i]
for j in range(self.o_n):
self.o_t[j] -= lr * o_grid[j]
for h in range(self.h_n):
self.h_t[h] -= lr * h_grid[h]# define TrainStandard() 函数
# 标准的BP函数,计算累积误差
def TrainStandard(self, data_in, data_out, lr=0.05):
'''
@param lr, learning rate, default 0.05
@param data_in :the networks input data
@param data_out:the output data of output layer
@return: e, accumulated error
@return: e_k, error array of each step
'''
e_k = []
for k in range(len(data_in)):
x = data_in[k]
y = data_out[k]
self.BackPropagate(x, y, lr)
# error in train set for each step
# 计算均方误差
y_delta2 = 0.0
for j in range(self.o_n):
y_delta2 += (self.o_v[j] - y[j]) * (self.o_v[j] - y[j])
e_k.append(y_delta2/2)
# total error of training
# 先计算出累积误差,然后最小化累积误差
e = sum(e_k)/len(e_k)
return e, e_k# 返回预测的标签,好瓜是1,坏瓜是0
def PredLabel(self, X):
'''
predict process through the network
@param X: the input sample set for input layer
@return: y, array, output set (0,1 - class) based on [winner-takes-all]
也就是竞争学习,胜者通吃
'''
import numpy as np
y = []
for m in range(len(X)):
self.Pred(X[m])
if self.o_v[0] > 0.5: y.append(1)
else : y.append(0)
# max_y = self.o_v[0]
# label = 0
# for j in range(1,self.o_n):
# if max_y < self.o_v[j]: label = j
# y.append(label)
return np.array(y)