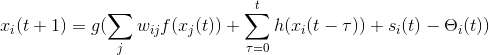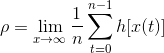混沌神经网络(Chaos Neural Network)
基本概念
吸引子:系统有朝着某个稳态发展的趋势,这个稳态就叫做吸引子。吸引子又分为平庸吸引子和奇异吸引子。
平庸吸引子:有不动点(平衡)、极限环(周期运动)和整数维环面(概周期运动)三种模式。(不动点:函数术语。函数经过有限次迭代回到相同的值的点为周期点,不动点是周期值为1的点。)
奇异吸引子:反应混沌系统运动特征的产物,是一种混沌系统中无需稳态的运动形态。奇异吸引子上的运动对初始值有着极强的敏感依赖性;奇异吸引子具有分维,如2.06维、1.2365维等,通常需要用计算来确定。
Hopfield神经网络:它是一种循环神经网络,从输出到输入有反馈连接。反馈神经网络由于其输出端又反馈到其输入端,所以,Hopfield网络在输入的激励下会产生不断的状态变化。当有输入之后,可以求取出Hopfield的输出,这个输出反馈到输入从而产生新的输出。这个反馈过程会一直进行下去。如果Hopfield网络是一个能收敛的稳定网络,则这个反馈与迭代的计算过程所产生的变化越来越小,一旦达到了稳定平衡状态,那么Hopfield网络就会输出一个稳定的恒值。对于一个Hopfield网络来说,关键是在于确定它在稳定条件下的权系数(无自反馈的权系数对称的Hopfield网络是稳定的网络)。 最早提出的是二值神经网络,也叫离散Hopfield神经网络。1表示激活状态,0表示抑制状态。
前馈网络的输出仅与当前输入与权矩阵决定,与网络先前输出状态无关,且通过引入隐层及非线性转移函数(激活函数)使网络具有复杂的非线性映射能力。前馈网络中,不论是离散还是连续,一般不考虑输入与输出之间在时间上的滞后性,只是表达两者间映射关系。但在Hopfield网络中,需考虑输入输出间的延迟因素,因此需要通过微分方程或差分方程描述网络的动态数学模型。Hopfield网络分为连续型和离散型,分别记为CHNN和DHNN。
常见CNN的设计
四种混沌神经网络的设计:
第一种思路是直接给每个神经元混沌性质,也就是说,换一个混沌迭代函数就相当于找到一种“新的”神经网络。混沌性质是通过显式或隐式迭代来实现的。通过混沌迭代,可以将神经元在一段连续的离散时刻t,t+1,t+2,...时刻的内部状态变量关联起来,并将其他所有的神经元输出加权和当作输入,得到的方程如下:
其中![]() 是神经元在t+1时的内部状态变量,输出的
是神经元在t+1时的内部状态变量,输出的![]() 由传输函数
由传输函数![]() 决定,
决定,![]() 为时滞函数,
为时滞函数,![]() 为外部输入,
为外部输入,![]() 为阈值,如果不考虑时滞,就会缺少第二项。
为阈值,如果不考虑时滞,就会缺少第二项。
第二种思路是直接对经典的神经网络进行改造,利用现有的学习算法,令经典的神经网络(比如 具有隐层的网络)来对混沌吸引子进行学习(如利用Ikeda混沌吸引子),让网络能够在一定程度上模拟混沌吸引子的轨道,再引入时延反馈控制等手段从而令网络能有混沌行为。
第三种思路是一般在Hopfield网络上进行改造,通过引入自反馈来使网络具有暂态混沌的能力。如L.Chen和Aihara提出的暂态混沌神经网络。
第四种思路是给神经元的内部状态变量强加某一种类型的混沌噪声。例如Hayakawa提出的混沌神经网络。
常见性质:
小世界网络:相对于同等规模节点的随机网络,拥有比较短的平均路径长度还有比较大的聚类系数特征的网络模型。
耦合:指两个或者两个以上的电路元件或电网络等的输入和输出之间有着紧密配合还有相互影响,并且通过相互作用从一侧向另一侧传输能量的现象。
联想记忆法:利用识记对象与客观现实的联系、已知与未知的联系、材料内部各部分之间的联系来记忆的方法。
模式识别:对表征事物或现象的各种形式的(数值的、文字的和逻辑关系的)信息进行处理和分析信息进行处理和分析,来对事物或者现象进行描述、辨认、分类以及解释的过程。
混沌模式识别:对任意模式,系统都能够正确地对这种模式进行分类,但系统的输出并不稳定在这个模式上,而是会呈现出相应的动态特性。
混沌神经网络“不稳定”,不能通过有监督学习和无监督学习来研究。
首次提出混沌神经网络的概念:Adachi神经网络
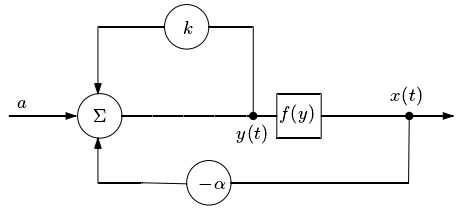
Adachi神经网络结构图:假设外部激励函数为常数a,神经元的内部状态变量为y(t),神经元在时刻t的输出为x(t),不应性反馈常数为α(通常为正值),不应性衰减因子为k。则可表示为:
![]()
单个神经元的模型为下图:
Adachi神经元模型和Nagumo-Sato神经元模型的重要区别是,Nagumo-Sato模型传输函数为阶跃函数,Adachi模型传输函数为Sigmoid函数。平均激活率的定义为:
超越方程:是指包含超越函数(指的是变量之间不能用有限次加、减、乘、除、乘方、开方运算表示的函数,如三角函数、对数函数、反三角函数、指数函数等等就是超越函数)的方程。
lyapunov(李雅普诺夫)指数:用来描述系统对初始值的极端敏感性。两个相差无几的初值所产生的轨迹,随着时间的推移按照指数方式进行分离,lyapunov指数就是用来定量描述这个现象的量。lyapunov指数可以衡量系统是否存在动力学混沌,正的lyapunov指数意味着在系统相空间中不管初始两条轨线的间距多么小,其差别都能随时间的演化成指数率增加而达到无法预测,这就是混沌现象。
任何一个神经网络都包含三个重要构件:神经元模型、学习算法和网络拓扑结构。
为了降低神经元之间连接的复杂性,尝试将Adachi神经网络由完全耦合结构改为线性结构。一棵具有N个节点的树仅有N-1条边。修改后的网络拓扑结构变成:任意两个神经元之间能通过生成树联系起来,连接所有神经元的总边数是N-1。改变了网络的拓扑结构,要用梯度搜索法(比较简单的算法,广泛应用于各类神经网络和机器学习)设置网络新的权值。
若Adachi网络受到的外部激励为已知模式,那么网络的输出将类似于周期轨道,利用这一点可以实现模式识别。混沌模式识别性质:对于一个已知的外部激励模式,输出和外部激励之间会产生“共鸣”,即在网络的动态演化过程中,输入的外部激励模式被频繁检索;而对于一个未知的外部激励模式,输出就呈现出混沌状态。
模式识别:就是通过计算机用数学技术方法来研究模式的自动处理和判读。是指对表征事物或现象的各种形式的(数值的、文字的和逻辑关系的)信息进行处理和分析,来对事物或现象进行描述、辨认、分类和解释的过程,是信息科学和人工智能的重要组成部分。
小世界网络:60年代美国学者Milgram通过社会调查得出的一项成果。世界上任何两个互不相识的人,平均来说,通过6个人就可以建立联系,通常也被称作为六度分离原则。Watts和Strogts对小世界网络进行了研究。构造方法:1、首先生成邻近耦合网络,每个节点和与其相邻的左右各k/2个节点相连。2、对网络中的每一条边,重复以下操作:断开之前的连接,用固定的概率P和网络中任意选择的一个节点相连。这个模型被称为WS模型。当p=1时,该网络就变成完全随机网络;当p=0时,网络仍然为临近耦合网络。
由于WS模型在进行重连接时可能会使一些节点孤立从而造成网络不连通,故Newman和Watts对这个模型做了相应的改动:1、首先生成邻近耦合网络,每个节点和与其相邻的左右各k/2个节点相连。2、用固定概率P在随机选择的两个节点之间加上一条边。这个模型为NW模型。当p=1时,该网络就变成了完全耦合网络;当p=0时,该网络保持不变,仍为邻近耦合网络。
NW模型与WS模型的最主要区别在于增边还是减边。从本质上讲,当随机重连概率或随机增加概率很小并且网络边数很大时,这两个模型是相同的。
SmallWorld-Adachi 网络具有较好的模式识别性质。在适当的参数设置下,当外部激励为已知模式时,网络的输出会与外部激励发生“共鸣”,即外部输入模式会被频繁识别,相反,其它模式却不出现;当外部激励为噪音模式时,与之对应的模式也会被识别,而噪音模式本身很少出现;当外部激励为未知模式时,网络不能将该激励与任何已知模式对应。
混沌神经网络
混沌神经网络如何从不稳定的轨道中提取信息,考虑两种方法。
频数统计:在迭代过程中,若网络的输出和某个记忆向量的Hamming距离为0(或接近0)的情况频繁出现,就可以认为该记忆向量被成功识别。若出现网络的输出和多个记忆向量的Hamming距离为0的情况,就认为Hamming距离为0出现最多的记忆向量被识别。
傅里叶分析:也需要计算Hamming距离。由于网络的输出和记忆向量之间的Hamming距离多数时会比较大,少数时较小或者为0,因此当Hamming距离由大变小时会有明显的“毛刺”,从而可以采用傅里叶分析手段提取出这些毛刺,进而可以判断网络是否对记忆向量进行了成功识别。而且傅里叶手段很成熟,不论采用硬件或软件都能实现,而且具有较高的效率。
混沌与加密的算法与思路:1、利用混沌系统生成伪随机序列,利用该序列作为密钥加密(通常是异或运算)明文信息流。这种算法可以归结到混沌流密码中去。2、利用明文和混沌系统的控制参数作为密钥,重复使用正向或反向的迭代来获取密文。这种算法可以归结到混沌分组密码中去。3、利用混沌系统的非线性性质,设计混沌S盒。将该S盒直接用于传统的分组密码中(例如DES)。4、利用驱动-响应的办法来达到混沌系统之间的同步,从而实现保密通信。具体思想是:在发送端,将信息和混沌信号一起调制成类似于噪声的波形;接收端从接收到的波形中解调恢复真正的信息。根据发送端调制、生成发送信号和接收端解调信号所采取策略的不同,可将利用混沌同步实现信息保密的方法分为以下几种:
(1)混沌调制类型:发送端利用混沌系统和待发送信息动态地生成发送信号,该信号可看成是混沌系统状态变量和信息信号的函数。发送信号传输到接收端作为驱动信号,实现接收端和发送端的同步,从而以逆函数的形式恢复信息信号。
(2)混沌键控系统:在发送端有多个混沌系统,根据要传送的码值选择不同的混沌系统,这样发送信号由一段段代表不同混沌吸引子的混沌信号组成。发送端的各个混沌系统在接收端有对应的同步系统。用接收的信号驱动各个同步系统,根据码元周期内各个同步系统达到同步的情况来判断这个周期内所传送的码值。
(3)参数调制的方式:用离散的或模拟的信息调制发送端混沌系统的一个或多个参数,信号传送到接收端后,以自适应方式实现同步,在达到同步的同时估计出时变的参数,并从参数中提取信息。
(4)利用混沌系统的符号动力学性质,采用混沌控制的方法,要求输出的混沌信号跟踪预定的符号序列,实现传输信号对预定信息的编码。在接收端对接收信号进行解码获得相应的信息,从而实现保密通信。
(5)差分混沌键控和混沌扩频等方式,利用混沌信号的自相关和互相关特性来满足特定的通信需求。
其中基于(1)-(3)的混沌密码算法被称为“数字”混沌密码算法,基于混沌同步的密码算法称为“模拟”混沌密码算法。
一些应用:https://blog.csdn.net/hey_mr_airplane/article/details/80347487
https://blog.csdn.net/hey_mr_airplane/article/details/80446430
转载自:hey_mr_airplane的相关文章