Arrays.toString(）和oString()区别,2进制怎样表示负数， 原码 2 反码 3. 补码,byte&oxff到底为什么 (byte) 0x97=-105：java 2进制补码

目录

Arrays.toString(）和oString()区别：

 

​

补充：String.getByte();就是将String的每一个字符串转化成AScii

并且byte存储只能是整形，小数进行取整；

​

1. 原码

2. 反码

3. 补码

为什么存在补码；

 (byte) 0x97=-105

---

Arrays.toString(）和oString()区别：

    public static String toString(byte[] a) {
        if (a == null)
            return "null";
        int iMax = a.length - 1;
        if (iMax == -1)
            return "[]";

        StringBuilder b = new StringBuilder();
        b.append('[');
        for (int i = 0; ; i++) {
            b.append(a[i]);
            if (i == iMax)
                return b.append(']').toString();
            b.append(", ");
        }
    }

 

测试：

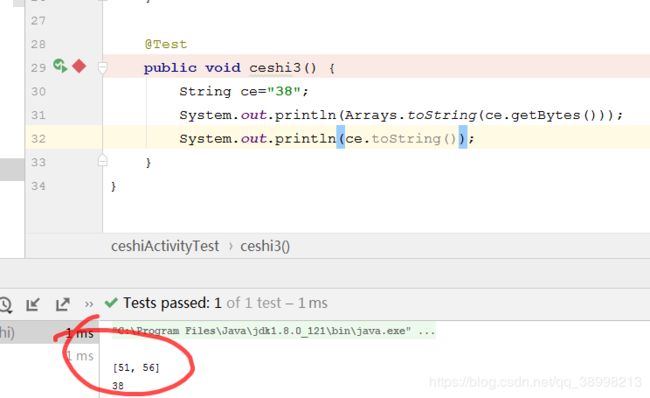
    @Test
    public void ceshi3() {
        String ce="38";
        System.out.println(Arrays.toString(ce.getBytes()));
        int aa=0x38;
        ce.toString();
        System.out.println(aa);
    }

补充：String.getByte();就是将String的每一个字符串转化成AScii

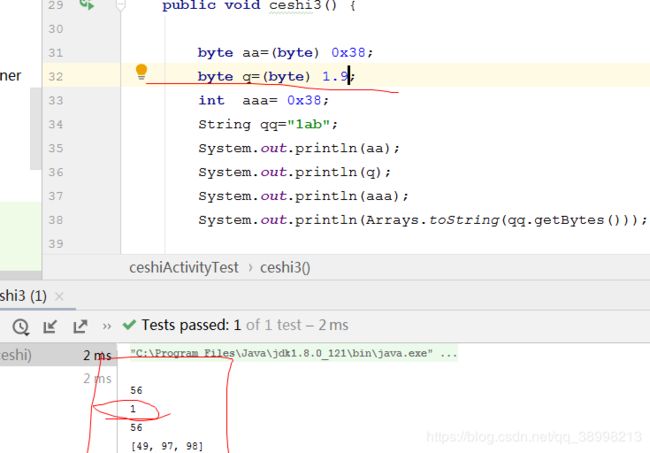
    @Test
    public void ceshi3() {

        byte aa=(byte) 0x38;
        byte q=(byte) 1;
        int  aaa= 0x38;
        String qq="1ab";
        System.out.println(aa);
        System.out.println(q);
        System.out.println(aaa);
        System.out.println(Arrays.toString(qq.getBytes()));

    }

并且byte存储只能是整形，小数进行取整；

1. 原码

原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

[+1]原 = 0000 0001

[-1]原 = 1000 0001

第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:

[1111 1111 , 0111 1111]

即：[-127 , 127]

2. 反码

反码的表示方法是:

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

[+1] = [00000001]原 = [00000001]反

[-1] = [10000001]原 = [11111110]反

可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.

3. 补码

正数的补码就是其本身

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1] = [10000001]原 = [11111110]反 = [11111111]补

 

为什么存在补码；

但对于二进制运算而言，原码的运算不够方便，当两个数相加时，先要判断这两个数的符号是否相同，符号不同的话，还要判断哪一个数的绝对值更大。所以在计算机中，通常都是采用补码形式。
正整数的补码与原码形式相同，例如+7的8位二进制补码是00000111；而负整数的补码则可以通过下列方式得到：将这个负整数的绝对值求反加1，连同符号位1一起表示就可以了。例如-7的8位二进制补码：将-7的绝对值7求反加1得1111001，连同符号位1一起就是11111001。
你也可以练习一下+13和-13的8位二进制补码：+13d=00001101，-13d=11110011。

 

 (byte) 0x97=-105

实际上在数值类型转换时，只有当遇到负数时才会出现问题，根本原因就是Java中的负数不是采用直观的方式进行编码，而是采用“2的补码”方式，这样的好处是加法和减法操作可以同时使用加法完成，但是在开发时却会遇到很多奇怪的问题，例如(byte)128的结果是-128，即一个大的正数，截断后却变成了负数。

下面这行代码的输出是什么？

public static void main(String[] args) {
  System.out.println(0xffffffff);
}

下面两行代码的输出相同吗？

public static void main(String[] args) {
  byte b=-1;
  System.out.println((int)(char)b);
  System.out.println((int)(char)(b & 0xff));
}

正如你所看到的：
第1个代码片段的运行结果是：-1
第2个代码片段的运行结果是：65535和255

public class Multicast{
  public static void main (String[] args){
    System.out.println((int)(char)(byte)-1);
  }
}

 

解释 举个简单的例子:

byte[]  b = new byte[5];

b[0] = -12;

byte   8位二进制   =   1个字节    char   2个字节   short (2个字节)    int（4个字节） long（8个字节） float  （4个字节） double（8个字节）

计算机存储数据机制：正数存储的二进制原码,负数存储的是二进制的补码。  补码是负数的绝对值反码加1。

比如-12，-12 的绝对值原码是：0000 1100  取反： 1111 0011  加1：  1111 0100

byte --> int   就是由8位变 32 位 高24位全部补1： 1111 1111 1111 1111 1111 1111 1111 0100 ;

0xFF 是计算机十六进制的表示： 0x就是代表十六进制，A B C D E F  分别代表10 11 12 13 14 15   F就是15  一个F 代表4位二进制：可以看做 是   8  4  2  1。

0xFF的二进制表示就是：1111 1111。   高24位补0：0000 0000 0000 0000 0000 0000 1111 1111;

-12的补码与0xFF 进行与（&）操作  最后就是0000 0000 0000 0000 0000 0000 1111 0100 

转换为十进制就是 244。

byte类型的数字要&0xff再赋值给int类型，其本质原因就是想保持二进制补码的一致性。

当byte要转化为int的时候，高的24位必然会补1，这样，其二进制补码其实已经不一致了，&0xff可以将高的24位置为0，低8位保持原样。这样做的目的就是为了保证二进制数据的一致性。

有人问为什么上面的式子中b[0]不是8位而是32位，因为当系统检测到byte可能会转化成int或者说byte与int类型进行运算的时候，就会将byte的内存空间高位补1（也就是按符号位补位）扩充到32位，再参与运算。
 

一、Java中如何编码负数？

    Java采用”2的补码“(Two's Complement)编码负数，它是一种数值的编码方法，要分二步完成：第一步，每一个二进制位都取相反值，0变成1，1变成0。比如，+8的二进制编码是00001000，取反后就是11110111。第二步，将上一步得到的值加1。11110111就变成11111000。所以，00001000的2的补码就是11111000。也就是说，-8在计算机（8位机）中就是用11111000表示。关于“2的补码”的详细信息，请参考阮一峰的博文《关于2的补码》，博文地址附在本文的参考部分。

二、什么是符号扩展(Sign Extension)?

    符号扩展（Sign Extension）用于在数值类型转换时扩展二进制位的长度，以保证转换后的数值和原数值的符号（正或负）和大小相同，一般用于较窄的类型（如byte）向较宽的类型（如int）转换。扩展二进制位长度指的是，在原数值的二进制位左边补齐若干个符号位（0表示正，1表示负）。

    举例来说，如果用6个bit表示十进制数10，二进制码为"00 1010"，如果将它进行符号扩展为16bits长度，结果是"0000 0000 0000 1010"，即在左边补上10个0（因为10是正数，符号为0），符号扩展前后数值的大小和符号都保持不变；如果用10bits表示十进制数-15，使用“2的补码”编码后，二进制码为"11 1111 0001"，如果将它进行符号扩展为16bits，结果是"1111 1111 1111 0001",即在左边补上6个1（因为-15是负数，符号为1），符号扩展前后数值的大小和符号都保持不变。

三、Java类型转换规则

1. Java中整型字面量   

 Java中int型字面量的书写方式有以下几种：

    - 十进制方式，直接书写十进制数字

    - 八进制方式，格式以0打头，例如012表示十进制10

    - 十六进制方式，格式为0x打头，例如0xff表示十进制255

 需要注意的是，在Java中012和0xff返回的都是int型数据，即长度是32位。

2. Java的数值类型转换规则

    这个规则是《Java解惑》总结的：如果最初的数值类型是有符号的，那么就执行符号扩展；如果是char类型，那么不管它要被转换成什么类型，都执行零扩展。还有另外一条规则也需要记住，如果目标类型的长度小于源类型的长度，则直接截取目标类型的长度。例如将int型转换成byte型，直接截取int型的右边8位。

四、解析“多重转型”问题

  连续三次类型转换的表达式如下：

(int)(char)(byte)-1

1. int(32位) -> byte(8位)

  -1是int型的字面量，根据“2的补码”编码规则，编码结果为0xffffffff，即32位全部置1.转换成byte类型时，直接截取最后8位，所以byte结果为0xff，对应的十进制值是-1.

2. byte(8位) -> char(16位)

  由于byte是有符号类型，所以在转换成char型（16位）时需要进行符号扩展，即在0xff左边连续补上8个1（1是0xff的符号位），结果是0xffff。由于char是无符号类型，所以0xffff表示的十进制数是65535。

3. char(16位) -> int(32位)

  由于char是无符号类型，转换成int型时进行零扩展，即在0xffff左边连续补上16个0，结果是0x0000ffff,对应的十进制数是65535。

五、几个转型的例子

  在进行类型转换时，一定要了解表达式的含义，不能光靠感觉。最好的方法是将你的意图明确表达出来。

  在将一个char型数值c转型为一个宽度更宽的类型时，并且不希望有符号扩展，可以如下编码：

int i = c & 0xffff;

  上文曾提到过，0xffff是int型字面量，所以在进行&操作之前，编译器会自动将c转型成int型，即在c的二进制编码前添加16个0，然后再和0xffff进行&操作，所表达的意图是强制将前16置0，后16位保持不变。虽然这个操作不是必须的，但是明确表达了不进行符号扩展的意图。

如果需要符号扩展，则可以如下编码：

int i = (short)c; //Cast causes sign extension

  首先将c转换成short类型，它和char是 等宽度的，并且是有符号类型，再将short类型转换成int类型时，会自动进行符号扩展，即如果short为负数，则在左边补上16个1，否则补上16个0.

  如果在将一个byte数值b转型为一个char时，并且不希望有符号扩展，那么必须使用一个位掩码来限制它：

char c = (char)(b & 0xff);

  (b & 0xff)的结果是32位的int类型，前24被强制置0，后8位保持不变，然后转换成char型时，直接截取后16位。这样不管b是正数还是负数，转换成char时，都相当于是在左边补上8个0，即进行零扩展而不是符号扩展。

  如果需要符号扩展，则编码如下：

char c = (char)b; //Sign extension is performed

此时为了明确表达需要符号扩展的意图，注释是必须的。

六、小结

    实际上在数值类型转换时，只有当遇到负数时才会出现问题，根本原因就是Java中的负数不是采用直观的方式进行编码，而是采用“2的补码”方式，这样的好处是加法和减法操作可以同时使用加法电路完成，但是在开发时却会遇到很多奇怪的问题，例如(byte)128的结果是-128，即一个大的正数，截断后却变成了负数。3.2节中引用了一些转型规则，应用这些规则可以很容地解决常见的转型问题。