非参数统计 作业(第五章第六章)
第五章 分类数据关联性分析
习题5.11
数据描述
本案例所用到的数据来源于问卷调查,目的是探究问卷各项满意度是否存在差异
分析思路
满意度为类变量,可进行Ridit分析,根据Ridit分析原理编写相应检验程序ridit.test,该函数返回每个处理的得分、95%置信区间、统计量W值以及Kruskal—Wallis检验p值。
分析过程
载入数据,分析数据结构
data<-read.csv(file="D:\\MyDownloads\\5.11.csv",header = T)
str(as.matrix(data))
int [1:5, 1:5] 90 47 20 28 34 20 34 13 32 28 ...
- attr(*, "dimnames")=List of 2
..$ : NULL
..$ : chr [1:5] "非常不满意" "不满意" "一般" "满意" ...
根据5.6节中Ridit检验法原理,编写ridit.test()函数
ridi.test<-function(x)
{
order.num=ncol(x)
treat.num=nrow(x)
rowsum=rowSums(x)#O_i.
colsum=colSums(x)#O_.i
total=sum(rowsum)
N=(colsum/2)[1:order.num]+c(0,(cumsum(colsum))[1:order.num-1])
ri=N/total#每个顺序类的得分
p_coni=x/outer(rowsum,rep(1,order.num),"*")##概率阵——i水平下属于第j顺序类的概率、
pi.=rowsum/total
score=p_coni%*%ri
confi_inter=matrix(c(score-1/sqrt(3*rowsum),score+1/sqrt(3*rowsum)))
if(length(rle(sort(ri))$lengths)==length(ri))#不打结
{
w=(12*total/(total+1)*sum(rowsum*(score-0.5)^2))
}
if(length(rle(sort(ri))$lengths)<=length(ri))#打结
{
tao<-rle(sort(ri))$lengths
T=1-sum(tao^3-tao)/(order.num^3-order.num)
w=(12*total/((total+1)*T))*sum(rowsum*(score-0.5)^2)}
pvalue=pchisq(w,treat.num-1,lower.tail = FALSE)
list(score,confi_inter=confi_inter,W=w,pvalue=pvalue)
}
options(digits = 4)##设结果为4位有效数字
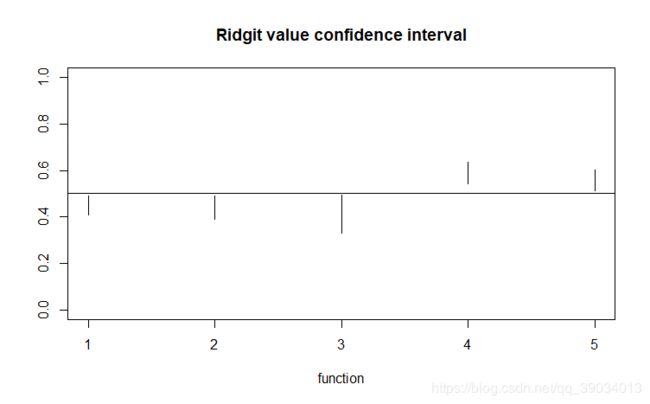
根据已编写的ridit.test()函数对已准备好的数据进行检验,并画出Ridit得分置信区间图·
res_data=ridi.test(as.matrix(data))
graph_data<-res_data$confi_inter
plot(0,0,ylim = c(0,1),xlim = c(1,5),xlab = "function",ylab = "",main="Ridgit value confidence interval",col="gray7")
abline(h=0.5)
for(i in 1:(nrow(graph_data)/2))lines(c(i,i),c(graph_data[i],graph_data[i+5]))
结论
| Riditscore | Confidence Interval | W | P-value | |
|---|---|---|---|---|
| 0.4492 | 0.409 | 0.4893 | 37.85 | 1.20E-07 |
| 0.439 | 0.3888 | 0.4893 | ||
| 0.411 | 0.3293 | 0.4926 | ||
| 0.5877 | 0.5412 | 0.6342 | ||
| 0.558 | 0.5129 | 0.6031 |
取alpha=0.05,故通过检验,即各项满意度之间的差别是显著的,由上图可知,问项4、5满意度比较高,问项1、2、3满意度较低
第六章 秩相关与分位数回归
习题 6.1
数据描述
该数据为各省份文盲率与人均GDP,目的是探究两个变量之间的关系
分析思路
可通过不同检验统计量Pearson、Spearman、Kendall辨别相关性,编写相应检验程序cor.pearson、cor.spearman,cor.kendall,函数返回每个检验的p值与相关系数。
分析过程
导入数据,对数据进行描述性统计分析
iliteracy<-c(7.33,10.80,15.60,8.86,9.70,18.52,17.71,21.24,23.20,14.24,13.82,17.97,10.00,10.15,17.05,10.94,20.97,16.40,16.59,17.40,14.12,18.99,30.18,28.48,61.13,21.00,32.88,42.14,25.02,14.65)
GDP<-c(15044,12270,5345,7730,22275,8447,9455,8136,6834,9513,4081,5500,5163,4220,4259,6468,3881,3715,4032,5122,4130,3763,2093,3715,2732,3313,2901,3748,3731,5167)
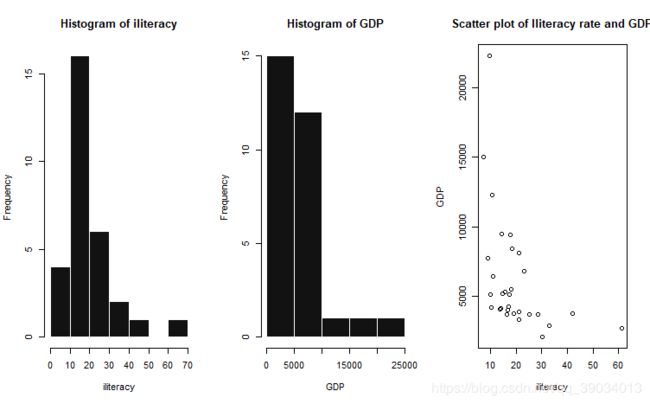
par(mfrow = c(1, 3))
hist(iliteracy,border = F,col = "gray7")
hist(GDP,border = F,col = "gray7")
plot(iliteracy,GDP,main="Scatter plot of Iliteracy rate and GDP")
观察上图猜测两变量间具有负相关性
编写cor.pearson、cor.spearman,cor.kendall函数
cor.pearson<-function(x,y)
{
x1<-x-mean(x)
y1<-y-mean(y)
numerator<-sum(x1*y1)
denominator<-sqrt(sum(x1^2)*sum(y1^2))
cor<-numerator/denominator
Z<-cor*sqrt(length(x)-2)/sqrt(1-cor^2)
p_value<-2*pt(Z,length(x)-2)
list(p_value=p_value,cor=cor)
}
cor.spearman<-function(x,y)
{
x.rank<-rank(x)
y.rank<-rank(y)
x1<-x.rank-mean(x.rank)
y1<-y.rank-mean(y.rank)
numerator<-sum(x1*y1)
denominator<-sqrt(sum(x1^2)*sum(y1^2))
cor<-numerator/denominator
Z<-cor*sqrt(length(x)-2)/sqrt(1-cor.test^2)
p_value<-2*pt(Z,length(x)-2)
list(p_value=p_value,cor=cor)
}
cor.kendall<-function(x,y)
{
options(digits = 4)
n<-length(x)
s=0
c=0
for(i in 1:(n-1)){
for(j in (i+1):n){
s=s+sign((iliteracy[i]-iliteracy[j])*(GDP[i]-GDP[j]))
c=c+1
}
}
tau <- 2/(n*(n-1))*s
Z <- tau*sqrt((9*n*(n-1))/(2*(2*n+5)))
p_value<-2*pnorm(Z)
list(p_value=p_value,cor=cor)
}
根据已编写的函数对已准备好的数据进行检验
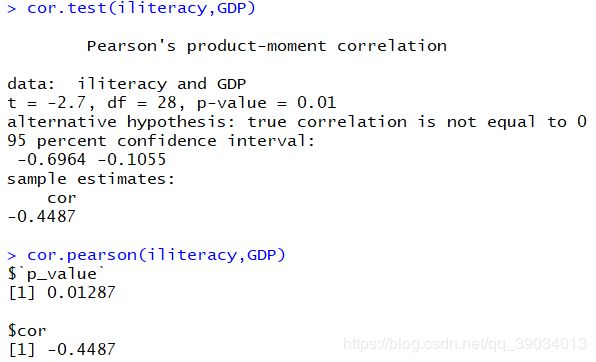
cor.test(iliteracy,GDP)
cor.pearson(iliteracy,GDP)
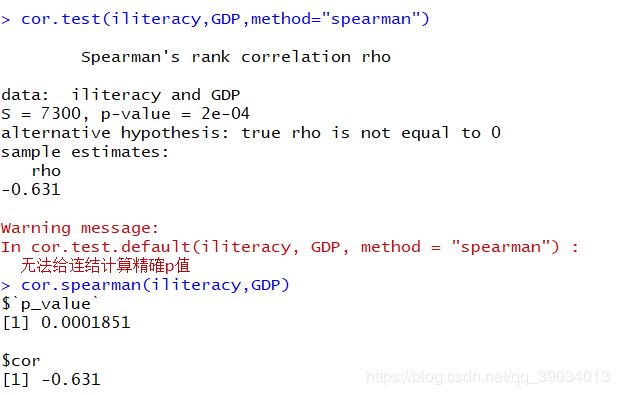
cor.test(iliteracy,GDP,method="spearman")
cor.spearman(iliteracy,GDP)
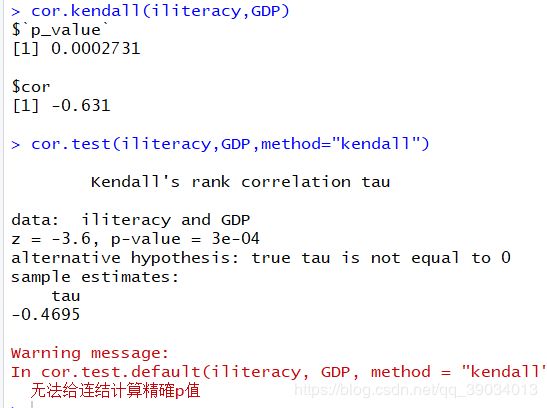
cor.kendall(iliteracy,GDP)
cor.test(iliteracy,GDP,method="kendall")
结果如下
Pearson检验
Kendall检验
结论
三种检验结果均拒绝原假设,均为负相关