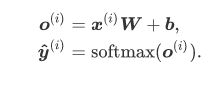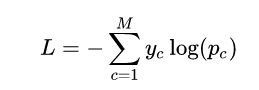动手学深度学习PyTorch版---day01

 

目录

Day01

1.线性回归

方法1---手动实现

方法2---pytorch实现

2.Softmax

1.相关概念

2.交叉熵损失函数

3.从零实现softmax回归

4.pytorch实现softmax回归

3.多层感知机

---

Day01

线性回归，softmax回归与分类模型，多层感知机

参考：https://tangshusen.me/Dive-into-DL-PyTorch/#/

《动手学深度学习》组队学习 学员学习手册  https://shimo.im/docs/pdr3wkyHKrxJYdyT/read

1.线性回归

方法1---手动实现

import torch
#import IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random

num_inputs = 2
num_examples = 1000

true_w = [2, -3,4]
true_b = 4.2

features = torch.randn(num_examples,num_inputs,
                       dtype=torch.float32) #标准正态分布
labels = true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                      dtype=torch.float32)
# plt.figure()
# #画散点图
# plt.scatter(features[:,1].numpy(),labels.numpy(),1)
# plt.show()

#读取数据
def data_iter(batch_size,features,labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i:min(i+batch_size, num_examples)])
        yield features.index_select(0, j), labels.index_select(0, j)

batch_size = 10
for X,y in data_iter(batch_size, features, labels):
    print(X,'\n', y)
    break

# 初始化模型参数
w = torch.tensor(np.random.normal(0,0.01,(num_inputs,1)),dtype=torch.float32)
b = torch.zeros(1,dtype=torch.float32)

w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

#定义模型
def linreg(X, w, b):
    return torch.mm(X,w)+b

#定义损失函数
def squared_loss(y_hat, y):
    return (y_hat-y.view(y_hat.size()))**2/2

#定义优化函数
def sgd(params, lr, batch_size):
    for param in params:
        param.data -= lr*param.grad/batch_size   #注意 .data

#train
lr = 0.03
num_epoches = 5

net = linreg
loss = squared_loss

for epoch in range(num_epoches):
    for X,y in data_iter(batch_size, features, labels):
        l = loss(net(X,w,b),y).sum()
        l.backward()
        sgd([w,b],lr,batch_size)
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b),labels)
    print('epoch %d, loss %f' % (epoch+1, train_l.mean().item()))

方法2---pytorch实现

import torch
from torch import nn
from torch.nn import init
import torch.optim as optim
import numpy as np
import torch.utils.data as Data

#生成数据
num_inputs = 2
num_examples = 1000

true_w = [2,-3.4]
true_b = 4.2

features = torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)),dtype=torch.float)
labels = true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
labels += torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float)

#读取数据集
batch_size=10
#combine features and labels of dataset
dataset = Data.TensorDataset(features, labels)
#put dataset into DataLoader
data_iter = Data.DataLoader(
    dataset=dataset,    #torch TensorDataset format
    batch_size=batch_size,
    shuffle=True,
    num_workers=0, #read data in multithreading
)
# for X,y in data_iter:
#     print(X,'\n',y)
#     break


#定义模型
class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(n_feature,1)

    def forward(self,x):
        y = self.linear(x)
        return y

    # 定义权值初始化
    def initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                torch.nn.init.normal_(m.weight.data, 0, 0.01)
                m.bias.data.zero_()

net = LinearNet(num_inputs)     #num_inputs传参n_feature
net.initialize_weights()
# print(net)

#loss
loss=nn.MSELoss()

#定义优化函数
optimizer = optim.SGD(net.parameters(),lr=0.03)
#print(optimizer)

#training
num_epoches=3
for epoch in range(1,num_epoches+1):
    for X,y in data_iter:
        output = net(X)
        l = loss(output,y.view(-1,1))
        optimizer.zero_grad()  #reset gradient
        l.backward()
        optimizer.step()
    print('epoch %d,loss %f' % (epoch, l.item()))

2.Softmax

1.相关概念

• softmax回归的输出层也是一个全连接层。

• softmax运算符，将输出值变换成值为正且和为1的概率分布
• 解决问题

• softmax回归对样本i分类的矢量计算表达式为

                                    

2.交叉熵损失函数

                               

3.从零实现softmax回归

import torch
import numpy as np

num_inputs = 784
num_outputs = 10

W = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_outputs)), dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float)
W.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

def softmax(X):
    X_exp = X.exp()
    partition = X_exp.sum(dim=1, keepdim=True)
    # print("X size is ", X_exp.size())
    # print("partition size is ", partition, partition.size())
    return X_exp / partition  # 这里应用了广播机制
X = torch.rand((2, 5))
X_prob = softmax(X)
print(X_prob, '\n', X_prob.sum(dim=1))

#softmax回归模型
def net(X):
    return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)

#定义损失函数
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.gather(1, y.view(-1, 1))

def cross_entropy(y_hat, y):
    return - torch.log(y_hat.gather(1, y.view(-1, 1)))

#定义准确率
def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum /n

def accuracy(y_hat, y):
    return (y_hat.argmax(dim=1) == y).float().mean().item()

4.pytorch实现softmax回归

import torch
from torch import nn
from torch.nn import init
import numpy as np

num_inputs = 784
num_outputs = 10

class LinearNet(nn.Module):
    def __init__(self, num_inputs, num_outputs):
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(num_inputs, num_outputs)

    def forward(self, x):  # x 的形状: (batch, 1, 28, 28)
        y = self.linear(x.view(x.shape[0], -1))
        return y


# net = LinearNet(num_inputs, num_outputs)

class FlattenLayer(nn.Module):
    def __init__(self):
        super(FlattenLayer, self).__init__()

    def forward(self, x):  # x 的形状: (batch, *, *, ...)
        return x.view(x.shape[0], -1)


from collections import OrderedDict

net = nn.Sequential(
    # FlattenLayer(),
    # LinearNet(num_inputs, num_outputs)
    OrderedDict([
        ('flatten', FlattenLayer()),
        ('linear', nn.Linear(num_inputs, num_outputs))])  # 或者写成我们自己定义的 LinearNet(num_inputs, num_outputs) 也可以
)

#初始化
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)

#loss
loss = nn.CrossEntropyLoss()

#优化函数
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)

3.多层感知机

1.sigmoid