LeetCode 实践练习1-5

LeetCode—1

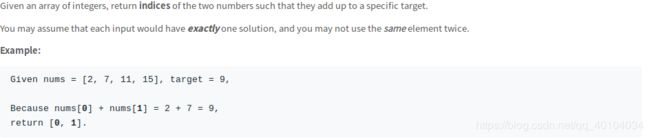
1.暴力法
遍历数组其余部分来进行来寻找所对应部分。时间复杂度为$O(n^2)$ 空间复杂度为$O(n)$
（疑问：每个不是利用了两次吗？）

public int[] twoSum(int[] nums, int target) {
    for (int i = 0; i < nums.length; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] == target - nums[i]) {
                return new int[] { i, j };
            }
        }
    }
    throw new IllegalArgumentException("No two sum solution");
}

2.两遍哈希表
利用哈希表将元素和索引，对应利用空间换时间。时间复杂度为$O(n)$ 空间复杂度为$O(n)$

public int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        map.put(nums[i], i);
    }
    for (int i = 0; i < nums.length; i++) {
        int complement = target - nums[i];
        if (map.containsKey(complement) && map.get(complement) != i) {
            return new int[] { i, map.get(complement) };
        }
    }
    throw new IllegalArgumentException("No two sum solution");
}

3.一遍哈希表
利用哈希表，在进行迭代进行插入元素同时，在同时检查表中是否含有满足条件的目标元素，有则立即返回。时间复杂度为$O(n)$ 空间复杂度为$O(n)$

public int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        int complement = target - nums[i];
        if (map.containsKey(complement)) {
            return new int[] { map.get(complement), i };
        }
        map.put(nums[i], i);
    }
    throw new IllegalArgumentException("No two sum solution");
}

Python_哈希解法

def twoSum(self, nums, target):
        d={}
        for i,num in enumerate(nums):
            if target-num in d:
            	return d[target-num],i
                #return d[target-num]+1, i+1 python数组从零索引开始
            d[num]=i

LeetCode—2

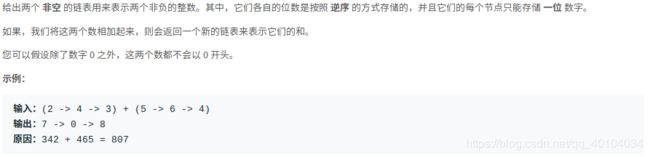
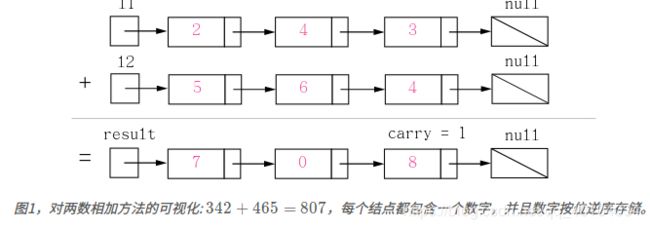思路：用变量跟踪进位，并从包含最低为有效位的表头开始模拟逐位相加的过程。
伪代码：

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    ListNode dummyHead = new ListNode(0);
    ListNode p = l1, q = l2, curr = dummyHead;
    int carry = 0;
    while (p != null || q != null) {
        int x = (p != null) ? p.val : 0;
        int y = (q != null) ? q.val : 0;
        int sum = carry + x + y;
        carry = sum / 10;
        curr.next = new ListNode(sum % 10);
        curr = curr.next;
        if (p != null) p = p.next;
        if (q != null) q = q.next;
    }
    if (carry > 0) {
        curr.next = new ListNode(carry);
    }
    return dummyHead.next;
}

python3-解法

class Solution:
    def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
        new = ListNode(0)
        n = new
        carry = 0
        while(l1 or l2):
            x = l1.val if l1 else 0
            y = l2.val if l2 else 0
            sum = x + y + carry
            carry = sum // 10
            n.next = ListNode(sum%10)
            n = n.next
            if(l1 != None):
                l1 = l1.next
            if(l2 != None):
                l2 = l2.next
        if (carry > 0):
            n.next = ListNode(carry)
        return new.next

时间复杂度：$O(max(m,n))$,空间复杂度$O(max(m,n))$
如果链表中的数字不是按逆序存储的呢？

LeetCode—3

方法一：暴力法（不推荐，太慢）
思路：逐个检查所有的子字符串，看它是否不含有重复的字符。
1.函数-枚举给定字符串所有子字符串
2.函数-查看一个字符串是否有重复字符

public class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length();
        int ans = 0;
        for (int i = 0; i < n; i++)
            for (int j = i + 1; j <= n; j++)
                if (allUnique(s, i, j)) ans = Math.max(ans, j - i);
        return ans;
    }

    public boolean allUnique(String s, int start, int end) {
        Set<Character> set = new HashSet<>();
        for (int i = start; i < end; i++) {
            Character ch = s.charAt(i);
            if (set.contains(ch)) return false;
            set.add(ch);
        }
        return true;
    }
}

时间复杂度：$O(n^3)$ 空间复杂度：$O(min(n,m))$

方法二：滑动窗口
使用HashSet作为滑动窗口，我们可以用$O(1)$的时间来完成对字符是否在当前的字符串中的检查。

public class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length();
        Set<Character> set = new HashSet<>();
        int ans = 0, i = 0, j = 0;
        while (i < n && j < n) {
            // try to extend the range [i, j]
            if (!set.contains(s.charAt(j))){
                set.add(s.charAt(j++));
                ans = Math.max(ans, j - i);
            }
            else {
                set.remove(s.charAt(i++));
            }
        }
        return ans;
    }
}

时间复杂度：$O(2n)=O(n)$, 空间复杂度：$O(min(m,n))$

方法三：优化的滑动窗口
方法二最多需要执行2n个步骤。事实上，他可以被进一步有为仅需要n个步骤。我们可以定义。我们可以定义字符到索引的映射，而不是使用集合来判断一个字符是否存在。 当我们找到重复的字符时，我们可以立即跳过该窗口。

public class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length(), ans = 0;
        Map<Character, Integer> map = new HashMap<>(); // current index of character
        // try to extend the range [i, j]
        for (int j = 0, i = 0; j < n; j++) {
            if (map.containsKey(s.charAt(j))) {
                i = Math.max(map.get(s.charAt(j)), i);//get根据键取值 跟窗口头索引比较
            }
            ans = Math.max(ans, j - i + 1);
            map.put(s.charAt(j), j + 1);
        }
        return ans;
    }
}

时间复杂度：$O(n)$, 空间复杂度：$O(min(m,n))$

python3-解法：

class Solution:
    # @return an integer
    def lengthOfLongestSubstring(self, s):
        start = maxLength = 0
        usedChar = {}
        
        for i in range(len(s)):
            if s[i] in usedChar and start <= usedChar[s[i]]:
                start = usedChar[s[i]] + 1
            else:
                maxLength = max(maxLength, i - start + 1)

            usedChar[s[i]] = i

        return maxLength

LeetCode—4

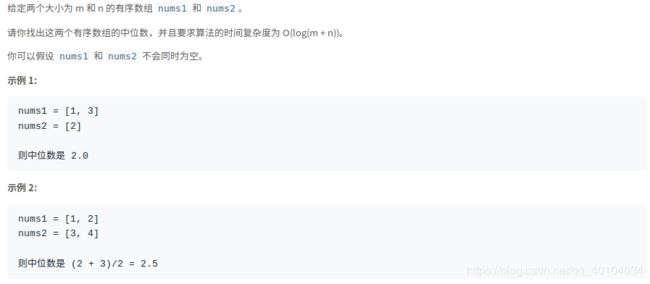自己的思路：先计算m+n为奇数还是偶数，奇数中位数索引则为[(m+n)/2],偶数索引则为(m+n)/2，（(m+n)/2）+1.在进行数组合并时，合并到索引处，得出中位数。
但是时间复杂度限制为$O(log(m+n))$,因此应该使用二分法来求解。应该是在两个数组之间使用二分法。
对于奇数与偶数的分情况讨论，可以使用一个小tirck，分别找第（m+n+1）/2,(m+n+2)/2,然后求其平均值。

好，这里我们需要定义一个函数来在两个有序数组中找到第K个元素，下面重点来看如何实现找到第K个元素。首先，为了避免产生新的数组从而增加时间复杂度，我们使用两个变量i和j分别来标记数组nums1和nums2的起始位置。然后来处理一些corner cases，比如当某一个数组的起始位置大于等于其数组长度时，说明其所有数字均已经被淘汰了，相当于一个空数组了，那么实际上就变成了在另一个数组中找数字，直接就可以找出来了。还有就是如果K=1的话，那么我们只要比较nums1和nums2的起始位置i和j上的数字就可以了。难点就在于一般的情况怎么处理？因为我们需要在两个有序数组中找到第K个元素，为了加快搜索的速度，我们要使用二分法，那么对谁二分呢，数组么？其实要对K二分，意思是我们需要分别在nums1和nums2中查找第K/2个元素，注意这里由于两个数组的长度不定，所以有可能某个数组没有第K/2个数字，所以我们需要先check一下，数组中到底存不存在第K/2个数字，如果存在就取出来，否则就赋值上一个整型最大值。如果某个数组没有第K/2个数字，那么我们就淘汰另一个数字的前K/2个数字即可。有没有可能两个数组都不存在第K/2个数字呢，这道题里是不可能的，因为我们的K不是任意给的，而是给的m+n的中间值，所以必定至少会有一个数组是存在第K/2个数字的。最后就是二分法的核心啦，比较这两个数组的第K/2小的数字midVal1和midVal2的大小，如果第一个数组的第K/2个数字小的话，那么说明我们要找的数字肯定不在nums1中的前K/2个数字，所以我们可以将其淘汰，将nums1的起始位置向后移动K/2个，并且此时的K也自减去K/2，调用递归。反之，我们淘汰nums2中的前K/2个数字，并将nums2的起始位置向后移动K/2个，并且此时的K也自减去K/2，调用递归即可，参见代码如下：

C++解法：

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size(), left = (m + n + 1) / 2, right = (m + n + 2) / 2;
        return (findKth(nums1, 0, nums2, 0, left) + findKth(nums1, 0, nums2, 0, right)) / 2.0;
    }
    int findKth(vector<int>& nums1, int i, vector<int>& nums2, int j, int k) {
        if (i >= nums1.size()) return nums2[j + k - 1];
        if (j >= nums2.size()) return nums1[i + k - 1];
        if (k == 1) return min(nums1[i], nums2[j]);
        int midVal1 = (i + k / 2 - 1 < nums1.size()) ? nums1[i + k / 2 - 1] : INT_MAX;
        int midVal2 = (j + k / 2 - 1 < nums2.size()) ? nums2[j + k / 2 - 1] : INT_MAX;
        if (midVal1 < midVal2) {
            return findKth(nums1, i + k / 2, nums2, j, k - k / 2);
        } else {
            return findKth(nums1, i, nums2, j + k / 2, k - k / 2);
        }
    }
};

python解法：

def median(A, B):
    m, n = len(A), len(B)
    if m > n:
        A, B, m, n = B, A, n, m
    if n == 0:
        raise ValueError

    imin, imax, half_len = 0, m, (m + n + 1) / 2
    while imin <= imax:
        i = (imin + imax) / 2
        j = half_len - i
        if i < m and B[j-1] > A[i]:
            # i is too small, must increase it
            imin = i + 1
        elif i > 0 and A[i-1] > B[j]:
            # i is too big, must decrease it
            imax = i - 1
        else:
            # i is perfect

            if i == 0: max_of_left = B[j-1]
            elif j == 0: max_of_left = A[i-1]
            else: max_of_left = max(A[i-1], B[j-1])

            if (m + n) % 2 == 1:
                return max_of_left

            if i == m: min_of_right = B[j]
            elif j == n: min_of_right = A[i]
            else: min_of_right = min(A[i], B[j])

            return (max_of_left + min_of_right) / 2.0

LeetCode—5

回文是一个正读和反读都相同的字符串.
方法一：最长公共子串
每当我们找到最长的公共子串的候选项时，都需要检查子串的索引是否与反向子串的原始索引相同，例如：子串为：abcd 反向 dcba 索引分别为1234 与 4321 不同，而abcba 索引为12321 反向为 12321.因此若相同，则更新母亲啊找到的最长回文子串；如果不是，我们就跳过这个候选项并继续寻找下一个候选。复杂度$O(n^2)$
方法二：暴力法
选出所有字符串的开始和结束位置，检验是不是回文（不推荐）时间复杂度$O(n^3)$,空间复杂度$O(1)$
方法三：动态规划
改进暴力法避免在验证回文是进行不必要的重复计算。
时间复杂度：$O(n^2)$. 空间复杂度:$O(n^2)$
方法四：中心扩展算法
利用恒定的空间，在$O(n^2)$时间内解决这个问题。
回文可以从它的中心展开，并且只有2n-1个这样的中心。
方法五：Manacher算法（马拉车算法）
Manacher算法
代码：

#include 
#include 
#include 

using namespace std;

string Manacher(string s) {
    // Insert '#'
    string t = "$#";
    for (int i = 0; i < s.size(); ++i) {
        t += s[i];
        t += "#";
    }
    // Process t
    vector<int> p(t.size(), 0);
    int mx = 0, id = 0, resLen = 0, resCenter = 0;
    for (int i = 1; i < t.size(); ++i) {
        p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while (t[i + p[i]] == t[i - p[i]]) ++p[i];
        if (mx < i + p[i]) {
            mx = i + p[i];
            id = i;
        }
        if (resLen < p[i]) {
            resLen = p[i];
            resCenter = i;
        }
    }
    return s.substr((resCenter - resLen) / 2, resLen - 1);
}

int main() {
    string s1 = "12212";
    cout << Manacher(s1) << endl;
    string s2 = "122122";
    cout << Manacher(s2) << endl;
    string s = "waabwswfd";
    cout << Manacher(s) << endl;
}