Pytorch 学习(三):Pytorch 线性回归模型实现
Pytorch 入门:线性回归实现
本方法源自《动手学深度学习》(Pytorch版)github项目
对于一个简单线性回归问题,使用 Pytorch 利用梯度下降法进行解决
问题陈述
对于公式 ![]() ,其中
,其中 ![]() 为公式参数的真值。现需要创建模拟数据、构建线性回归模型并对参数进行梯度求解。
为公式参数的真值。现需要创建模拟数据、构建线性回归模型并对参数进行梯度求解。
实验过程
- 创建
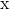 和
和 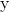 的数据,随机生成 1000 个
的数据,随机生成 1000 个 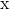 样本,根据公式计算出
样本,根据公式计算出 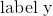 并添加随机噪声,编写 batch 的数据读取方式
并添加随机噪声,编写 batch 的数据读取方式 - 构建线性回归计算过程、损失函数、SGD 梯度下降过程并对参数
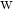 和
和 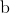 初始化
初始化 - 利用梯度下降进行迭代计算
代码实现
方法一:先造轮子再上车,从盘古开天辟地开始说起
import torch
import numpy as np
import random
true_w = [2.0, -3.4]
true_b = 4.2
num_inputs = 2
num_examples = 1000
# 1000 个样本构建
features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
labels = features.mm(torch.tensor(true_w).view(2, 1)) + true_b
# 添加均值为 0,方差为 0.01 的随机噪声给 y,从而对其进行拟合
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)
# 构建以 batch 为单位的数据
batch_size = 10
def batch_iter(batch_size, features, labels):
nums = len(features)
indices = list(range(nums))
random.shuffle(indices)
for i in range(0, nums, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size, nums)])
yield features.index_select(0, j), labels.index_select(0, j)
# yield 以迭代器的形式返回
# index_select(dim, indices) 选取 dim 维度上的 indices 数据
# 构建线性回归模型
def linearReg(w, b, X):
return X.mm(w) + b
def square_loss(y_, y):
return (y_ - y) ** 2 / 2.0
def SGD(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad_fn / batch_size
# 通过 .data 改变梯度不会影响梯度回传的值
# w, b intilization
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32, requries_grad=True)
b = torch.ones(1, dtype=torch.float32, requries_grad=True)
# 迭代下降
lr = 0.03
epochs = 3
net = linearReg
loss = square_loss
for epo in range(1, epochs + 1):
for X, y_ in batch_iter(batch_size, features, labels):
y = net(w, b, X)
l = loss(y_, y)
l.backward() # 梯度回传
SGD([w, b], lr, batch_size) # 梯度下降
# 梯度清零
w.gard.data.zero_()
b.gard.data.zero_()
train_l = loss(net(w, b, features), labels)
print('epoch: %d, loss: %f' % (epo, train_l))
# 查看拟合结果
print('w: [%f, %f], b: %f' % (w[0].item(), w[1].item(), b.item()))
方法二:先上车再说话,我是调包侠
import torch
import torch.nn as nn
import torch.utils.data as Data
import torch.optim as optim
from torch.nn import init
true_w = [2.0, -3.4]
true_b = 4.2
# 相似的数据构造
num_inputs = 2
num_examples = 1000
features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
labels = features.mm(torch.tensor(true_w).view(2, 1)) + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)
# 调用函数创建 batch 形式的数据
batch_size = 10
dataset = Data.TensorDataset(features, labels)
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
# 构建线性回归模型
class linearNet(nn.module):
def __init__(self, n_features):
super(linearNet, self).__init__()
self.linear = nn.linear(n_features, 1)
def forward(x):
return self.linear(x)
loss = nn.MSEloss()
optimizer = optim.SGD(net.parameters(), lr=0.03)
# w, b intilization
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)
# 叠加下降
net = linearNet(num_inputs)
epochs = 3
for epo in range(1, epochs + 1):
for X, y_ in data_iter:
y = net(X)
l = loss(y_, y.view(-1, 1))
optimizer.zero_grad() # 梯度清零
l.backward() # 梯度回传
optimizer.step() # 梯度下降
print('epoch: %d, loss: %f' % (epo, l.item()))