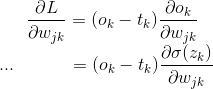机器学习：自己动手实现神经网络，从感知机（perceptron）到多层神经网络

一、神经网络的由来

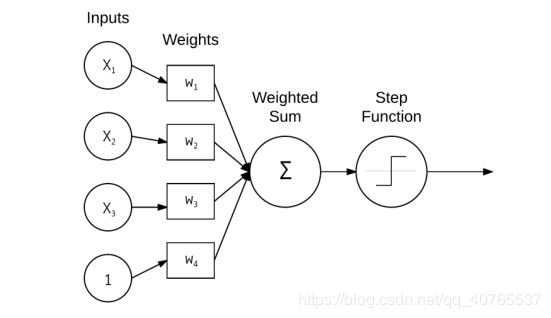
1958年，感知机(Perception)模型横空出世，在上个世纪一度掀起一股AI热。

感知机实际上是一个线性的模型，可以理解成只有一层的神经网络。

代码实现：

import numpy as np

class Perceptron:
    def __init__(self, N, alpha=0.1):
        self.W = np.random.randn(N+1)/np.sqrt(N)
        self.alpha = alpha

    def step(self, x):
        return 1 if x > 0 else 0
    
    def fit(self, X, y, epochs=10):
        # 在训练数据后面添加一列1来模拟bias   (X_n)(W_n)+b <=> (X_n+1)(W_n+1)
        X = np.c_[X, np.ones((X.shape[0]))]
        for epoch in np.arange(0, epochs):
            for (x, target) in zip(X,y):
                p = self.step(np.dot(x, self.W))

                if p != target:
                    error = p-target
                    self.W += - self.alpha * error * x
    
    def predict(self, X, addBias=True):
        #保证X至少是二维的数组
        X = np.atleast_2d(X)

        if addBias:
            X = np.c_[X,np.ones((X.shape[0]))]
        
        return self.step(np.dot(X, self.W))

但是感知机是有缺陷的，它不能处理XOR型的数据，在下面的第三个图中无法找到一条线（超平面）把不同类别的数据区分开。

 二、多层神经网络

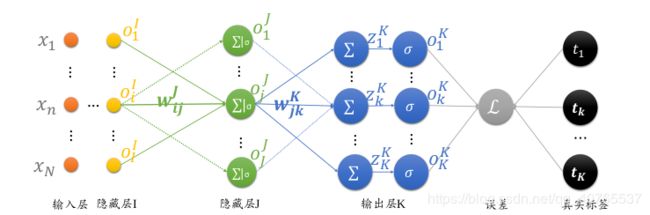
多层神经网络的训练主要是有两个步骤，前向传播（the forward pass，feedforward）和反向传播（the backward pass， backpropagation）。多层神经网络会比单层的复杂，一个是前向传播更多层，一个是反向传播的求偏微分比较复杂，反向传播算法也称为BP算法。

考虑下面这样的网络

 因为神经网络训练的过程就是参数w更新的过程，对于任意参数 ，我们想要让它：

L就是损失函数，alpha是学习率，通过这样更新参数，可以使Loss不断变小

所以问题就聚焦在了怎么求偏微分上，定义损失函数为方差square loss

对于参数来说，它的偏微分就是

sigmoid函数的导数 就是 可以自己简单去推一下，带入上式可得

上面的公式中省去了上标，上标的意思代表第几层，这里的公式推导是倒数第一层，即上标为K的层。

类似的，我们可以反向倒数第二层的参数的偏微分，再把图放一次：

根据链式法则，有：

再用后面的结果带入前面的公式得到：

通过定义变量,每一层的梯度表达式变得更加清晰简洁,其中可以简单理解为当前连接对误差函数的贡献值。

类似的可以求各层的偏微分。

实现：

neuralnetwork.py

import numpy as np 

class NeuralNetwork:
    def __init__(self, layers, alpha=0.1):
        self.W = []
        self.layers = layers
        self.alpha = alpha
        for i in np.arange(0, len(layers)-2):
            # 随机初始化一个权重矩阵，将每个层的节点数连接在一起，为偏置bias添加一个位
            w = np.random.randn(layers[i] + 1, layers[i+1] + 1)
            self.W.append(w / np.sqrt(layers[i]))
        # 最后两层是比较特殊的，因为最后一层是输出，不需要添加偏置bias
        w = np.random.randn(layers[-2] + 1, layers[-1])
        self.W.append(w / np.sqrt(layers[-2]))
    
    def __repr__(self):
        # 返回一个字符串显示神经网络的结构
        return "NeuralNetwork:{}".format("-".join(str(l) for l in self.layers))
    
    def sigmoid(self,x):
        return 1.0 / (1 + np.exp(-x))
    
    def sigmoid_deriv(self, x):
        # compute the derivative of the sigmoid function ASSUMING
        # that ‘x‘ has already been passed through the ‘sigmoid‘
        # function
        return x*(1-x)
    
    def fit(self, X, y, epochs=1000, displayUpdate=100):
        X = np.c_[X, np.ones((X.shape[0]))]

        for epoch in np.arange(0, epochs):
            for (x, target) in zip(X, y):
                self.fit_partial(x, target)
            
            if epoch == 0 or (epoch + 1) % displayUpdate == 0:
                loss = self.calculate_loss(X, y)
                print("[INFO] epoch={}, loss={:.7f}".format(
                    epoch + 1, loss))
    
    def fit_partial(self, x, y):
        # 将一维的数组或者单个的数转化为三维的数组
        A = [np.atleast_2d(x)]
        for layer in np.arange(0, len(self.W)):
            net = A[layer].dot(self.W[layer])

            out = self.sigmoid(net)
            A.append(out)
        # 反向传播的第一个阶段是计算
        # 预测值(激活列表中的最终输出激活)和真实目标值之间的差异               
        error = A[-1] - y
        # 从这里开始，我们需要应用链式法则，并构建我们的delta ' D '列表;
        # delta中的第一个项就是输出层的误差乘以我们对输出值的激活函数的导数
        D = [error * self.sigmoid_deriv(A[-1])]
        for layer in np.arange(len(A)-2, 0, -1):
            delta = D[-1].dot(self.W[layer].T)
            delta = delta * self.sigmoid_deriv(A[layer])
            D.append(delta)
        D = D[::-1]   #将D逆序

        for layer in np.arange(0, len(self.W)):
            self.W[layer] += -self.alpha*A[layer].T.dot(D[layer])

    def predict(self, X, addBias=True):
        p = np.atleast_2d(X)

        if addBias:
            p = np.c_[p, np.ones((p.shape[0]))]
        
        for layer in np.arange(0, len(self.W)):
            p = self.sigmoid(np.dot(p, self.W[layer]))
        
        return p
    
    def calculate_loss(self, X, targets):
        targets = np.atleast_2d(targets)
        predictions = self.predict(X, addBias=False)
        loss = 0.5 * np.sum((predictions-targets)**2)
        return loss

 test.py

from neuralnetwork import NeuralNetwork
import numpy as np

X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([[0],[1],[1],[0]])

nn = NeuralNetwork([2,2,1], alpha=0.5)
nn.fit(X,y,epochs=10000)

for (x, target) in zip(X, y):
    pred = nn.predict(x)[0][0]
    step = 1 if pred>0.5 else 0
    print("[INFO] data={}, ground-truth={},pred={:.4f},step={}".format(
        x, target[0], pred, step))


输出：
[INFO] epoch=1, loss=0.5106667
[INFO] epoch=100, loss=0.4977335
[INFO] epoch=200, loss=0.4918748
...
[INFO] epoch=9800, loss=0.1258784
[INFO] epoch=9900, loss=0.1258671
[INFO] epoch=10000, loss=0.1258561
[INFO] data=[0 0], ground-truth=0,pred=0.0104,step=0
[INFO] data=[0 1], ground-truth=1,pred=0.9824,step=1
[INFO] data=[1 0], ground-truth=1,pred=0.9824,step=1
[INFO] data=[1 1], ground-truth=0,pred=0.5010,step=1

 

参考资料：

https://segmentfault.com/a/1190000021529971