开关变换器小信号建模
DCDC变换器建模
- 一、开关电源建模基本概念
- 二、CCM下变换器建模
- 1.状态平均的概念
- 2.推导变换器的状态空间平均方程
- 3.对变换器的状态空间平均方程进行线性化处理
- 4.平均开关模型
- 三、DCM下变换器建模
- 1.DCM下变换器的状态空间平均方程
- 2.对状态空间平均方程进行线性化处理
- 四、基于电流峰值控制的CCM变换器建模
- 1.电流峰值控制的概念
- 2.峰值电流控制的稳定性问题
- 3.一阶模型
- 五、基于电流峰值控制的DCM变换器建模
- 1.建立状态平均模型
- 2.对状态平均模型进行线性化处理
在开关电源领域,建立变换器模型,分析变换器模型特点,选择合适的补偿网络,进行环路分析,从而理论上设计出一个稳定的电源,验证其动态、稳态指标满足需求,这样一套完整步骤很重要。《电力电子系统建模及控制》一书对 建立变换器模型这一步进行了详细分析,有时间的读者建议阅读原书学习。
一、开关电源建模基本概念
阅读本文之前,读者要具备一些基本知识
- DC/DC变换器系统的构成。
- 什么是一个电路拓扑的状态量,状态量方程如何推导。
二、CCM下变换器建模
读完本节,读者要能回答以下问题:
- 什么是状态平均?为什么要用状态平均方法?状态平均方法的特点与缺陷?
- 为什么需要对状态方程线性化与添加扰动分离小信号?
- 简述基于状态平均法建立反激电源小信号模型的步骤。
- 简述基于平均开关法建立反激电源小信号模型的步骤。
1.状态平均的概念
DC/DC变换器包含非线性元件,是一个非线性系统,不容易分析。但当变换器运行在某一稳态工作点附近,电路状态量的小信号扰动量之间呈现线性关系。因此,尽管DC变换器为非线性系统,但在研究它在某一稳态工作点附近的动态特性时,仍把它当做线性系统来近似,这就要用到状态空间平均的概念。
具体而言,当系统工作在某一稳态工作点,控制信号出现一个低频扰动时,变换器输出电压也被低频调制。输出电压中低频交流分量与控制信号低频扰动幅值成正比,频率相同,这就是线性电路的特征。
那么,当控制信号出现一个低频扰动时,输出电压里面只有低频量么?
实际上,由于要经过高频PWM调制,输出电压中除直流和低频交流分量外,还有开关频率(及其边带)和开关频率谐波(及其边带)成分。当开关频率较高、谐波幅值较低时,开关频率量的能量才可以忽略,这时候小信号的扰动量间的关系才近似为线性关系了。
在数学表达式上如何实现忽略开关频率量呢?答案如下:对某个量进行开关周期平均运算,将保留信号中低频部分,而滤除开关频率成分,定义这种运算为开关周期平均算子
![]()
状态量电感电流、电容电压经开关周期平均算子后仍然满足电磁感应定律。

利用开关周期平均算子表示的电路方程就是状态空间平均方程。
2.推导变换器的状态空间平均方程
以反激变换器为例推导其状态空间平均方程(大信号方程),反激电源电路结构如下。

详细推导步骤如下:
- 第一步,基于开关周期平均算子定义式列写电路状态量方程,如下所示:

- 第二步,基于开关周期平均算子的定义式,对方程变形推导

- 第三步,整理上式

- 至此,我们得到了反激电源的状态空间平均方程。可以发现,方程中存在变量 d(t)、d’(t) 与状态变量IL 、UG、U 的乘积项,属于非线性方程,无法采用经典控制理论,使用起来不方便,因此需要对方程进行线性化处理。
3.对变换器的状态空间平均方程进行线性化处理
若反激电源工作在某一静态工作点,占空比 、输入电压、电感电流、电容电压、输入电流的稳态值分别为D、Ug、IL、Uo、Ig。带入到状态空间平均方程,求解出稳定工作点各物理量之间的关系:
![]()
然后用扰动法求解小信号动态模型。如果对输入电压和占空比在直流工作点附近叠加微小扰动,即
![]()
于是将引起反激变换器电路中各状态变量和输出量的微小扰动,也即
![]()
将上式带入到状态空间平均方程(以及输入电流方程),消去直流稳态项,忽略二阶交流项(两个扰动量相乘认为是无穷小项),得到反激电源线性化小信号交流模型。

4.平均开关模型
基于数学方法的状态空间平均方法计算复杂,而且不直观。如果通过电路变换,求得小信号交流模型,将更为直观,使用起来更方便,这就是平均开关模型的出发点。
平均开关模型的理论依据是这样的:任一DC/DC变换器可分割成两个子电路,一个子电路为线性定常电路(电感、电容、电阻组成的电路),另一个为开关网络。前者在电路变换中无需进行处理、后者如何变换成线性定常电路是关键。
以反激电源为例进行分析,具体步骤如下:
第一步,首先将其按照线性定常电路与开关网络进行分割。

第二步:使用受控源等效开关网络子电路。

第三步:应用扰动法,分离直流项与二阶交流项,得到线性化处理后的电路。

第四步:将副边绕组折合到原边绕组。
三、DCM下变换器建模
读完本节,读者要能回答以下问题:
- DCM下变换器建模与CCM有什么不同?
- 简述DCM下反激电源的建模过程
1.DCM下变换器的状态空间平均方程
下面以反激变换器为例加以介绍。将反激电源如图绘制,图中虚线框部分构成一个二端口网络。DCM状态有三个模态d1、d2、d3。前两模态与CCM一致,d3期间电感电流发生断续。

![]()
详细建模过程如下:
- 步骤1 推导二端口开关网络的输入电压平均值
在DCM方式下,即使在暂态过程中,电感电压在一个开关周期中的平均值也为零,由此可得:

输入端口电压u1(t)一个开关周期中的平均值为:

将d2和d3用d1表示,化简上述方程,推导出二端口开关网络的输入电压平均值等于电源电压平均值。
![]()
2. 步骤2 推导二端口开关网络的输入电流平均值

定义
![]()
与之对比,我们回顾下CCM方式下输入端口方程,这里也体现了DCM状态与CCM状态有何不同。
![]()
3. 步骤3 推导二端口开关网络的输出电压平均值
步骤同步骤一,过程略。
![]()
5. 步骤4 推导二端口开关网络的输出电流平均值

观察上述方程,可见输出端口的输出功率等于输入端口的输入功率,即二端口开关网络没有功率损耗。
至此,我们求出了反激电源原边电压、电流,副边电压、电流之间满足的关系式。
6. 步骤5 绘制DCM反激变换器开关周期平均模型

将前文推导出来的表达式绘制到图中,得到上图所示的反激电源开关周期平均模型。列写出二端口开关网络的状态空间平均方程如下,可以发现,方程中存在d(t)与v(t)的乘积项,属于非线性方程,无法采用经典控制理论,使用起来不方便,因此需要对方程线性化。

2.对状态空间平均方程进行线性化处理
若反激电源工作在某一静态工作点,由二端口网络功率平衡得到:
![]()
然后用扰动法求解小信号动态模型。在直流工作点附近叠加微小扰动,并进行泰勒展开即

忽略泰勒级数展开的高阶项,然后消去直流项,得到输入端口方程:
![]()
类似地对于输出端口方程作同样处理,推导出输出端口方程为:

绘制出端口网络模型:

在实际应用中,通常忽略小信号模型中的电感,这样可以使得其模型大为简化。
令 Rp=r2//R(r2是输出端口内阻、R是负载阻抗),推导出控制至输出的传递函数以及输入至输出传递函数。


上面推导过程中,匝比概念被隐去了。在匝比为1下推导没问题,匝比不为1时要对哪些概念进行修正呢?
四、基于电流峰值控制的CCM变换器建模
读完本节,读者要能回答以下问题:
- 什么是峰值电流控制?控制框图的构成?简述控制机理?
- 峰值电流控制的稳定性问题?
- 什么是CPM一阶模型?一阶模型框图的构成?一阶模型的适用条件?
1.电流峰值控制的概念
电流峰值控制(CPM)中,用通过功率管的电流波形替代普通PWM调制电路中的载波信号,与控制输出相比较,以获得PWM调制信号。
下图给出反激电源采用电流峰值控制的原理图,每个开关周期之初,由时钟脉冲置位RS锁存器,导通开关;当电感电流增大至调制信号,比较器复位RS锁存器,关断开关。

2.峰值电流控制的稳定性问题
3.一阶模型
 首先绘制峰值电流控制的系统框图,内环采用电流峰值控制,外环采用电压补偿网络的系统框图如上图。为设计电压环,需先建立内环动态模型。
首先绘制峰值电流控制的系统框图,内环采用电流峰值控制,外环采用电压补偿网络的系统框图如上图。为设计电压环,需先建立内环动态模型。
对峰值电流控制的机理做适当假设,可以简化模型建立的复杂程度。例如这里,我们假设当变化器工作于CCM状态,可以忽略电感电流纹波,假定电感电流完全跟踪指令电流,即内环(闭环)传递函数为iL=ic 。将iL=ic 带入原模型(反激电源线性化小信号方程)并消去占空比 ,得到

为了求控制至输出传递函数,再令ug=0 ,于是可求得:

五、基于电流峰值控制的DCM变换器建模
读完本节,读者要能回答以下问题:
1.简述DCM下峰值电流控制的反激电源的建模过程。
1.建立状态平均模型
尽管一阶模型可以较快建立模型,展开后续设计。但一阶模型忽略了电感纹波和补偿锯齿波,因此仅适用于电感电流纹波较小,同时补偿锯齿波电流斜率较小的场合。实际上,当电感电流脉动较大,电感电流平均值与电流指令之间差异较大,一阶模型不再适用。一个极端的例子就是当工作在电流断续方式时,电感电流平均值只有电流指令的一半以下,显然,与一阶模型差别很大。
前文已经推导了DCM反激变换器的模型建立,本节分析采用电流峰值控制时,模型建立过程有何不同,详细步骤如下。

-
步骤1 推导二端口开关网络的输入端口方程
二端口开关网络的输入电流开关周期平均值为:

电流峰值控制下,电流指令与占空比满足以下关系:

结合两式,化简得到:
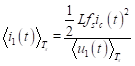
-
步骤2 推导二端口开关网络的输出端口方程
二端口开关网络的输入电流开关周期平均值为:

电流峰值控制下,电流指令与占空比满足以下关系:

结合两式,化简得到:

-
步骤3 整理上式

上述状态空间的开关周期平均值方程是反激电源断续模态下基于峰值电流控制的状态空间平均方程。可以发现,方程中存在变量之间 的乘积项,属于非线性方程,无法采用经典控制理论,使用起来不方便,因此需要对方程线性化。
2.对状态平均模型进行线性化处理
若反激电源工作在某一静态工作点,电流指令 ic=Ic,带入到状态空间平均方程,求解出稳定量的关系式:
![]()
![]()
首先引入扰动,然后在静态工作点附近作泰勒级数展开,例如对于输出端口,可以得到:

忽略泰勒级数展开的高阶项,然后消去直流项,得到输出端口的交流小信号线性方程:

又有副边绕组侧,负载的交流小信号线性方程如下(直接由电路得到):
![]()
对输出端口与负载方程联立求解,消去i2(s) ,最终得到:




