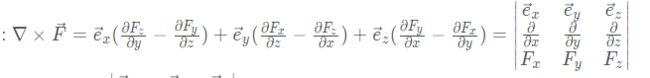电磁场考前总结
第一章公式整理
第二章公式整理(并没有整理多少)
概念
标量：一个只用大小描述的物理量。
矢量：一个既有大小又有方向特性的物理量。
矢量的几何表示：一个矢量可用一条有方向的线段来表示 。
场：确定空间区域上的每一点都有确定物理量与之对应，称在该区域上定义了一个场。
等值面：标量场取得同一数值的点在空间形成的曲面。
如果两个不为零的矢量的点积等于零，则此两个矢量必然相互 正交 。
标量场的梯度是一标量 场，表示某一点处标量场的 变化率。
方向导数表示场沿某方向的空间变化率
梯度描述标量场在某点的最大变化率及其变化最大的方向
电荷 是产生电场的源， 电流 是产生磁场的源。
电荷守恒定律:电荷既不能被创造，也不能被消灭，只能从物体的一部分转移到另一部分，或者从一个物体转移到另一个物体。
电介质的分子分为 无极 分子和 有极 分子。
在电场作用下，介质中无极分子的束缚电荷发生位移，有极分子的固有电偶极矩的取向趋
于电场方向，这种现象称为电介质的 极化
无极分子的极化称为 位移 极化，有极分子的极化称为 取向 极化
判断
- 单位矢量是常矢量。(错)
矢量的模和方向都不随空间坐标变化而变化的矢量为常矢量。单位矢量是指模等于1的向量。
- 标量场的等值面可以相交。(错)
同一个点不可能有两个物理量
- 矢量叉乘满足交换律(错)
- 矢量点乘满足结合律(错)
如我们所知，点乘是投影，
所以不满足结合律
- 静电场是无旋场，故电场强度沿任一条闭合路径的积分为零(对)
重要公式定理
几个重要计算
1. e ⃗ A = A ∣ A ∣ \vec{e}_A=\frac{A}{|A|} eA=∣A∣A
2. ∣ A ⃗ − B ⃗ ∣ |\vec{A}-\vec{B}| ∣A−B∣注意是模
3. A ⃗ ⋅ B ⃗ \vec{A}\cdot\vec{B} A⋅B点乘后是个值(标量)
4. c o s θ A B = A ⃗ ⋅ B ⃗ ∣ A ⃗ ∣ ∣ B ⃗ ∣ cos\theta_{AB}=\frac{\vec{A}\cdot\vec{B}}{|\vec{A}||\vec{B}|} cosθAB=∣A∣∣B∣A⋅B, θ A B = c o s − 1 A ⃗ ⋅ B ⃗ ∣ A ⃗ ∣ ∣ B ⃗ ∣ \theta_{AB}=cos^{-1}\frac{\vec{A}\cdot\vec{B}}{|\vec{A}||\vec{B}|} θAB=cos−1∣A∣∣B∣A⋅B
5.A在B上的分量
A B = ∣ A ⃗ ∣ c o s θ A B = A ⃗ ⋅ B ⃗ ∣ B ⃗ ∣ A_B=|\vec{A}|cos\theta_{AB}=\frac{\vec{A}\cdot\vec{B}}{|\vec{B}|} AB=∣A∣cosθAB=∣B∣A⋅B
6.叉积
叉积计算公式
注意:中间一个值做矩阵时要带符号
- 距离矢量：用末点减初点得到的矢量
- 点乘即投影，如求某矢量在x上的分量，就将该矢量点乘 e ⃗ x \vec{e}_x ex即可
- 求某矢量与x，y，z的夹角，用
将A替换成某矢量，B替换成 e ⃗ x \vec{e}_x ex， e ⃗ y \vec{e}_y ey， e ⃗ z \vec{e}_z ez即可
补充公式:
第一第二都是分配律
第三是转换
第四个可以记忆成先将B单独拿出来，中间量B为正，其余两个任意组合
- 坐标系转换
三个坐标系的转换画个图就知道了
直角(x,y,z)
圆柱( ρ , ϕ , z \rho,\phi,z ρ,ϕ,z)
球( r , θ , ϕ r,\theta,\phi r,θ,ϕ)
圆柱和球里的 ϕ \phi ϕ是一样的，都是xy平面的偏角， θ \theta θ是俯仰角
`
- 方向余弦
即矢量与x，y，z的夹角
- 梯度是最大变化率方向
梯度求解公式，哈密顿算子和标量函数结合
求某一方向的方向导数，先算出标量场的梯度，然后点乘该方向单位矢量，即在该方向上的投影。
- 散度的物理意义是单位闭合面内通过的矢量
求解方式就是点乘
- 旋度的物理意义是旋涡源密度矢量
求解方式:叉积
- 求解过程中会涉及到坐标的转换(重要！)
几个重要公式，散度定理，斯托克斯定理，格林公式要看一下，不过估计考不到
真是课堂造航母，考试拧螺丝
第二章
几个重要定理
库仑（Coulomb）定律(1785年)
真空中静止点电荷 q1 对 q2 的作用力:
F ⃗ 12 = e ⃗ R q 1 q 2 4 π ε 0 R 12 2 = q 1 q 2 R ⃗ 12 4 π ε 0 R 12 3 \vec{F}_{12}=\vec{e}_R\frac{q_1q_2}{4\pi\varepsilon_0R^2_{12}}=\frac{q_1q_2\vec{R}_{12}}{4\pi\varepsilon_0R^3_{12}} F12=eR4πε0R122q1q2=4πε0R123q1q2R12
静电场的散度（微分形式）：
∇ ⋅ E ⃗ ( r ⃗ ) = ρ ( r ⃗ ) ε 0 \nabla\cdot \vec{E}(\vec{r})=\frac{\rho(\vec{r})}{\varepsilon_0} ∇⋅E(r)=ε0ρ(r)(推导见书P43)
静电场的高斯定理(积分形式)：
∮ S E ⃗ ( r ⃗ ) ⋅ d S ⃗ = 1 ε 0 ∫ V ρ ( r ⃗ ) d V \oint_S \vec{E}(\vec{r})\cdot d\vec{S}=\frac{1}{\varepsilon_0}\int_V\rho(\vec{r})dV ∮SE(r)⋅dS=ε01∫Vρ(r)dV
高斯定理表明：静电场是有源场，电场线起始于正电荷，终止于负电荷。
静电场的旋度（微分形式）：
∇ × E ⃗ ( r ⃗ ) = 0 \nabla\times \vec{E}(\vec{r})=0 ∇×E(r)=0
静电场的环路定理(积分形式)：
∫ c E ⃗ ( r ⃗ ) ⋅ d l ⃗ = 0 \int_{c}\vec{E}(\vec{r})\cdot d\vec{l}=0 ∫cE(r)⋅dl=0
环路定理表明:静电场是无旋场，是保守场，电场力做功和路径无关
实验表明，真空中的载流回路C1对 载流回路C2的作用力
F ⃗ 12 = μ 0 4 π ∫ C 2 ∫ C 1 I 2 d l ⃗ 2 × ( I 1 d l ⃗ 1 × R ⃗ 12 ) R 12 3 \vec{F}_{12}=\frac{\mu_0}{4\pi}\int_{C_2}\int_{C_1}\frac{I_2d\vec{l}_2\times(I_1d\vec{l}_1\times\vec{R}_{12})}{{R}_{12}^3} F12=4πμ0∫C2∫C1R123I2dl2×(I1dl1×R12)
恒定场的散度(微分形式)：
∇ ⋅ B ⃗ ( r ⃗ ) = 0 \nabla\cdot\vec{B}(\vec{r})=0 ∇⋅B(r)=0
磁通连续性原理(积分形式):
∫ S B ⃗ ( r ⃗ ) ⋅ d S ⃗ = 0 \int_S\vec{B}(\vec{r})\cdot d\vec{S}=0 ∫SB(r)⋅dS=0
磁通连续性原理表明：恒定磁场是无源场，磁场线是无起点和终点的闭合曲线
恒定磁场的旋度(微分形式):
∇ × B ⃗ ( r ⃗ ) = μ 0 J ⃗ ( r ⃗ ) \nabla\times\vec{B}(\vec{r})=\mu_0\vec{J}(\vec{r}) ∇×B(r)=μ0J(r)
安培环路定理(积分形式):
∮ C B ⃗ ( r ⃗ ) ⋅ d l ⃗ = μ 0 ∫ S J ⃗ ( r ⃗ ) ⋅ d S ⃗ = μ 0 I \oint_{C}\vec{B}(\vec{r})\cdot d\vec{l}=\mu_0\int_{S}\vec{J}(\vec{r})\cdot d\vec{S}=\mu_0I ∮CB(r)⋅dl=μ0∫SJ(r)⋅dS=μ0I
安培环路定理表明:恒定磁场是有旋场，是非保守场，电流是磁场的漩涡源
电流连续性方程
积分形式: ∮ S J ⃗ ⋅ d S = − d q d t = − d d t ∫ V ρ d V \oint_S \vec{J}\cdot dS=-\frac{dq}{dt}=-\frac{d}{dt}\int_V\rho dV ∮SJ⋅dS=−dtdq=−dtd∫VρdV
(流出闭合面S的电流等于体积V内单位时间所减少的电荷量)
微分形式: ∇ ⋅ J ⃗ = − ∂ ρ ∂ t \nabla\cdot\vec{J}=-\frac{\partial \rho}{\partial t} ∇⋅J=−∂t∂ρ
极化强度矢量 P ⃗ = x e ε 0 E ⃗ \vec{P}=x_e\varepsilon_0\vec{E} P=xeε0E
任意闭合曲面电位移矢量 D 的通量等于该曲面包含自由电荷的代数和
∇ ⋅ D ⃗ = ρ \nabla \cdot \vec{D}=\rho ∇⋅D=ρ
其积分形式为 ∮ S D ⃗ ⋅ d S ⃗ = ∫ V ρ d V \oint_S\vec{D}\cdot d\vec{S}=\int_V\rho dV ∮SD⋅dS=∫VρdV