城市交通咨询模拟系统，利用该系统实现至少两种最优决策：最短路程到达、最省时到达等线路规划。

1．任务：设计一个城市交通咨询模拟系统，利用该系统实现至少两种最优决策：最短路程到达、最省时到达等线路规划。
2．内容：
用户驾车出行由于出行目的的不同对道路路线选择的要求也有不同。例如，有的希望在途中的路程尽可能短，有的则可能希望路程中时间最短。为了能满足广大旅客的需求，编制一个城市交通咨询模拟系统，选取城市部分位置、道路抽象为程序所需要图的顶点和边，并以城市道路长度（路程），道路的某时段的速度等信息作为图结点中的弧信息，为旅客提供这两种最优决策的交通咨询。

1、主要数据类型与变量

1.1 顶点，边，图的存储结构，还有宏定义，定点最大数，和无穷大

#define MAX_VERTEX_NUM 9  //顶点最大个数
#define INF 999 //代表无穷大
typedef struct {
    int no; //顶点编号
    char info; //顶点信息
}VertexType; //顶点类型
typedef struct GNode *PtrToGNode;

typedef struct GNode{
    double edges[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//领接矩阵的定义
    int n,e;//顶点数和边数
    VertexType vex[MAX_VERTEX_NUM];//存放定点的信息
}Mgraph;
typedef PtrToGNode MGraph;

typedef struct ENode *PtrToENode;
struct ENode {
    int V1, V2; /* 有向边 */
    double Weight; /* 权重km */
    int speed;/* 速度km/h */
};
typedef PtrToENode Edge;
1.2静态全局成员（目的：调用和修改方便）
dist数组，存放最短路径
static double dist[MAX_VERTEX_NUM];
Path数组，存放每个节点的前驱节点
static int path[MAX_VERTEX_NUM];
存放速度的二维数组，方便图中对应的坐标能找到对应的速度
static int speed[MAX_VERTEX_NUM][MAX_VERTEX_NUM];

1.3函数结构说明
typedef PtrToENode Edge;
/**
 * 迪杰特斯拉最短路径算法
 * @param g 领接矩阵的图
 * @param v 起始顶点
 * @param dist 存放V到每个节点的最短路径的数组
 * @param path 存放每个节点的前驱节点
 */
void Dijkstra(Mgraph g,int v,double dist[],int path[]);
/**
 * 目的是通过键盘输入创建图
 * @return
 */
MGraph BuildGraph();
/**
 * 通过输入的顶点数初始化图，方便BuildGraph函数调用
 * @param VertexNum 顶点数
 * @return 返回初始化成功的图
 */
MGraph CreateGraph( int VertexNum );
/**
 * 打印dist和path两个数组
 */
void printMap();
/**
 * 目的是在边图中增加速度的数据
 * @param g 原来没有速度的图
 * @param speed 跟图一样的数组，但是对应的坐标存放的是速度
 */
void addSpeed(Mgraph *g,int speed[][MAX_VERTEX_NUM]);
/**
 * 把最后关键的数据，返回到文件中，然后通过数据展示构建图在前端页面上
 * @param path 存放的路径
 * @param data 存放的数据
 */
void writeFile(string path,string data);

2、算法或程序模块
2.1 程序流程解释：
①创建图（领接矩阵）：通过输入顶点数，边数，每条边的起点终点，每条边对应的速度，通过BuildGraph函数构造出来。
②通过迪杰特斯拉算法求出最短路径，将dist和path数组的数据记录一下，然后增加二维数组speed存放图的每个坐标所对应的速度，在通过T=S/V的公式计算出每条边所需要的时间（代替原来的路程），然后再使用一次迪杰特斯拉算法求出最短时间。
③输出两次记录的dist和path数组到前端页面，通过前端和数据构建出图的样式，最短路径和最短时间为红色，否则为绿色。
核心函数解释
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
MGraph CreateGraph( int VertexNum )
{ Vertex V, W;
    MGraph Graph;
    Graph = (MGraph )malloc(sizeof(MGraph));
    Graph->n = VertexNum;
    Graph->e = 0;
/* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for (V=0; V<Graph->n; V++)
        for (W=0; W<Graph->n; W++)
            Graph->edges[V][W] = INF; /* 或INFINITY */
    return Graph;
}

MGraph BuildGraph()
{ MGraph Graph;
    Edge E = (Edge)malloc(MAX_VERTEX_NUM * sizeof(struct ENode));
    int  V;
    int Nv, i;
    cout<<"请输入定点数"<<endl;
    scanf("%d", &Nv);
    Graph = CreateGraph(Nv);
    cout<<"请输入总边数"<<endl;
    scanf("%d", &(Graph->e));
    if ( Graph->e != 0 ) {
        for (i=0; i<Graph->e; i++) {
           cout<<"请输入边的信息，from，to，和权重"<<endl;
            scanf("%d %d %lf",&E->V1, &E->V2, &E->Weight);
            cout<<"请输入速度："<<endl;
            scanf("%d",&speed[E->V1][E->V2]);
            /* 插入边  */
            Graph->edges[E->V1][E->V2] = E->Weight;
        }
    }
/* 如果顶点有数据的话，读入数据 */
 /*   for (V=0; Vn; V++){
        scanf(" %c", &(Graph->vex[V]));
    }*/
    return Graph;
}
void Dijkstra(Mgraph g,int v,double dist[],int path[]){
    int i,j,u;
    double min;
    bool collected[MAX_VERTEX_NUM];
    /*从这句开始对各数组进行初始化*/
    for (int i = 0; i < g.n; ++i) {
        dist[i] = g.edges[v][i];
        collected[i] = false;
        if(g.edges[v][i]<INF)
            path[i] = v;
        else
            path[i] = -1;
    }
    collected[v] = true; path[v] = -1;
    for (int k = 0; k < g.n-1; ++k) {
        min = INF;
        //v = 未收录顶点中dist的最小者
        for (int i = 0; i < g.n; ++i) {
            //如果该点没有被收录，且路径小于当前的最小值
            if(collected[i]==false && dist[i]<min){
                u=i;
                min = dist[i];
            }
        }
        collected[u] = true; //将选出的点并入最短路径中
        //如果不存在，则break
        for (int i = 0; i < g.n; ++i) {
            /*这个if语句判断顶点u的加入是否会出现通往顶点j的更短的路径，如果出现，则改变原来路径及其长度，否则什么都不做*/
            if(collected[i]==false && dist[u]+g.edges[u][i] < dist[i]){
                dist[i] = dist[u]+g.edges[u][i];
                path[i] = u; //更新前面的节点
            }
        }
    }
}

主程序main函数
int main(){
    MGraph graph = (MGraph )malloc(sizeof(MGraph)); 
    graph= BuildGraph(); //建图
    Dijkstra(*graph,0,dist,path); //求最短路径
    ... 
    addSpeed(graph,speed);//增加速度
    Dijkstra(*graph,0,dist,path);//求最短时间
    ...
}

三、测试

1、方案
方案：根据指导书上的图结点创建图。


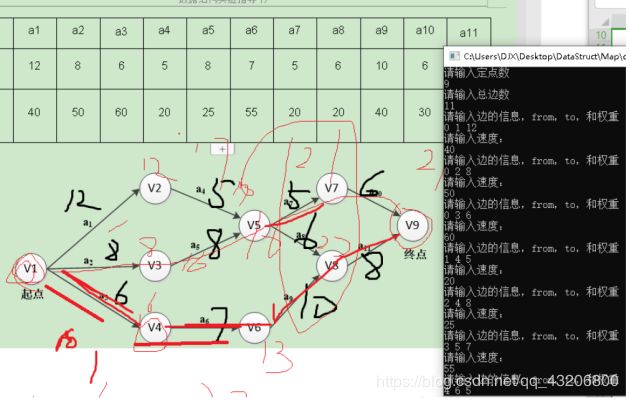
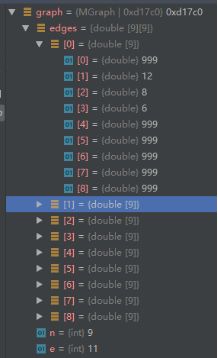
成功创建图结点
2、结果（第一个是最短路径的dist和path数组，第二个是最短时间的dist和path数组）

最后将这些数据传输到前端，方便展示到达目的地的最短路径和最短时间，手动选择目的地将会根据path数组把经过的结点标记为橙色

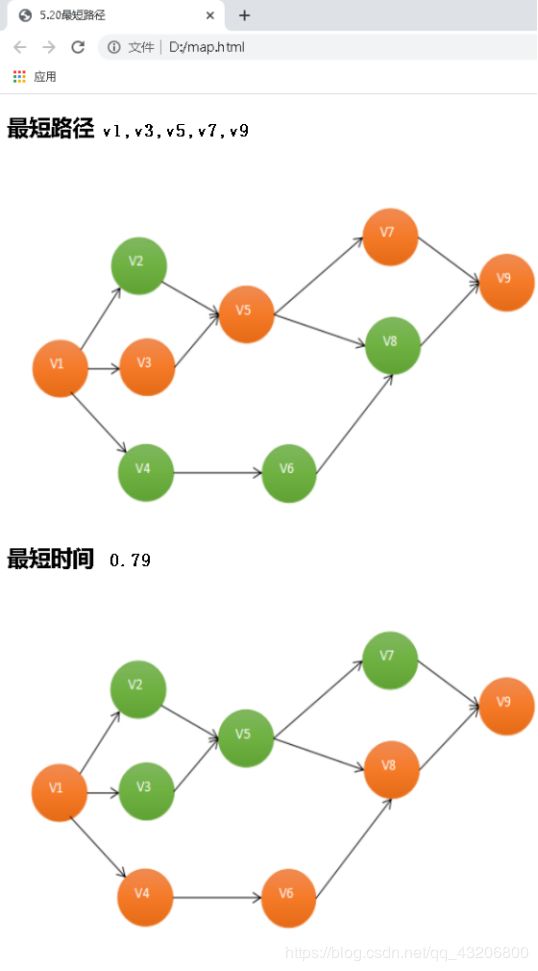
结果检验：
手动笔算最短路径和最短时间看是否与之输出结果对应。
V1->v9:最短路径27，最短时间约等于8/10。
结果与之对应，正确。

四、总结与讨论

本次实验主要我主要运用了迪杰特斯拉算法来求带权图的最短路径和最短时间，此算法理解时容易，但通过代码实现的时候会遇到很多不理想的情况，比如需要通过bool类型数组确定节点是否被收录过，通过dist和path数组来交替赋值，细节上慢慢改动才成功实现了该算法，然后求最短时间加入了一个二维数组来代替每条边的速度。
遇到的问题：①数据类型的定义，在求最短时间时，使用int型的路程、速度、领接矩阵然后通过公式T=S/V算出来的值不精确，导致结果错误，后来改动为double类型才正确②单独开一个二维数组存放时间增加了空间复杂度，再进行第二次迪杰特斯拉算法也增加时间复杂度，应该在设计边节点时加入速度，然后使用领接表比较好弄，不过因为设计的时候选了领接矩阵所以不好改动③在进行数据输出为图像的时候使用了前端的知识，起初选中的顶点不会变色，后来自己查询了相关的css知识使之成功变橙色。

程序的源代码
#include 
#include 
#include 
#include 
using namespace std;

#define MAX_VERTEX_NUM 9  //顶点最大个数
#define INF 999
typedef struct {
    int no; //定点编号
    char info; //定点信息
}VertexType; //定点类型
typedef struct GNode *PtrToGNode;

typedef struct GNode{
    double edges[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//领接矩阵的定义
    int n,e;//顶点数和边数
    VertexType vex[MAX_VERTEX_NUM];//存放定点的信息
}Mgraph;
typedef PtrToGNode MGraph;

typedef struct ENode *PtrToENode;
struct ENode {
    int V1, V2; /* 有向边 */
    double Weight; /* 权重km */
    int speed;/* 速度km/h */
};
typedef PtrToENode Edge;
/**
 * 迪杰特斯拉最短路径算法
 * @param g 领接矩阵的图
 * @param v 起始顶点
 * @param dist 存放V到每个节点的最短路径的数组
 * @param path 存放每个节点的前驱节点
 */
void Dijkstra(Mgraph g,int v,double dist[],int path[]);
/**
 * 目的是通过键盘输入创建图
 * @return
 */
MGraph BuildGraph();
/**
 * 通过输入的顶点数初始化图，方便BuildGraph函数调用
 * @param VertexNum 顶点数
 * @return 返回初始化成功的图
 */
MGraph CreateGraph( int VertexNum );
/**
 * 打印dist和path两个数组
 */
void printMap();
/**
 * 目的是在边图中增加速度的数据
 * @param g 原来没有速度的图
 * @param speed 跟图一样的数组，但是对应的坐标存放的是速度
 */
void addSpeed(Mgraph *g,int speed[][MAX_VERTEX_NUM]);
/**
 * 把最后关键的数据，返回到文件中，然后通过数据展示构建图在前端页面上
 * @param path 存放的路径
 * @param data 存放的数据
 */
void writeFile(string path,string data);

static double dist[MAX_VERTEX_NUM];
static int path[MAX_VERTEX_NUM];
static int speed[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
void test(int dist[]);
int main(){
    MGraph graph = (MGraph )malloc(sizeof(MGraph));
    graph= BuildGraph();
    Dijkstra(*graph,0,dist,path);
    writeFile("D:\\map.txt",dist);
    addSpeed(graph,speed);
    Dijkstra(*graph,0,dist,path);
    writeFile("D:\\map.txt",dist);
}
// 写文件
void writeFile(string path,double data)
{
    //1、创建输出流对象，并打开
    ofstream ofs(path,ios::out);
    //2、写文件
    for (int i = 0; i < MAX_VERTEX_NUM; ++i) {
        ofs<<data<<endl;
    }
    //3、关闭文件
    ofs.close();
}
void addSpeed(Mgraph *g,int speed[][MAX_VERTEX_NUM]){
    for (int i = 0; i < g->n; ++i)
        for (int j = 0; j < g->n; ++j) {
            if(g->edges[i][j]!=INF && speed[i][j]!=0){
                double t =(g->edges[i][j]/(speed[i][j]*1.0));
                g->edges[i][j] = t;
            }
        }
}

typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
MGraph CreateGraph( int VertexNum )
{ Vertex V, W;
    MGraph Graph;
    Graph = (MGraph )malloc(sizeof(MGraph));
    Graph->n = VertexNum;
    Graph->e = 0;
/* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
    for (V=0; V<Graph->n; V++)
        for (W=0; W<Graph->n; W++)
            Graph->edges[V][W] = INF; /* 或INFINITY */
    return Graph;
}



MGraph BuildGraph()
{ MGraph Graph;
    Edge E = (Edge)malloc(MAX_VERTEX_NUM * sizeof(struct ENode));
    int  V;
    int Nv, i;
    cout<<"请输入定点数"<<endl;
    scanf("%d", &Nv);
    Graph = CreateGraph(Nv);
    cout<<"请输入总边数"<<endl;
    scanf("%d", &(Graph->e));
    if ( Graph->e != 0 ) {
        for (i=0; i<Graph->e; i++) {
           cout<<"请输入边的信息，from，to，和权重"<<endl;
            scanf("%d %d %lf",&E->V1, &E->V2, &E->Weight);
            cout<<"请输入速度："<<endl;
            scanf("%d",&speed[E->V1][E->V2]);
            /* 插入边  */
            Graph->edges[E->V1][E->V2] = E->Weight;
        }
    }
/* 如果顶点有数据的话，读入数据 */
 /*   for (V=0; Vn; V++){
        scanf(" %c", &(Graph->vex[V]));
    }*/
    return Graph;
}

void Dijkstra(Mgraph g,int v,double dist[],int path[]){
    int i,j,u;
    double min;
    bool collected[MAX_VERTEX_NUM];
    /*从这句开始对各数组进行初始化*/
    for (int i = 0; i < g.n; ++i) {
        dist[i] = g.edges[v][i];
        collected[i] = false;
        if(g.edges[v][i]<INF)
            path[i] = v;
        else
            path[i] = -1;
    }
    collected[v] = true; path[v] = -1;
    for (int k = 0; k < g.n-1; ++k) {
        min = INF;
        //v = 未收录顶点中dist的最小者
        for (int i = 0; i < g.n; ++i) {
            //如果该点没有被收录，且路径小于当前的最小值
            if(collected[i]==false && dist[i]<min){
                u=i;
                min = dist[i];
            }
        }
        collected[u] = true; //将选出的点并入最短路径中
        //如果不存在，则break
        for (int i = 0; i < g.n; ++i) {
            /*这个if语句判断顶点u的加入是否会出现通往顶点j的更短的路径，如果出现，则改变原来路径及其长度，否则什么都不做*/
            if(collected[i]==false && dist[u]+g.edges[u][i] < dist[i]){
                dist[i] = dist[u]+g.edges[u][i];
                path[i] = u; //更新前面的节点
            }
        }
    }
}