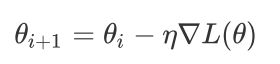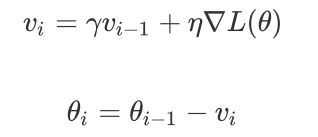神经网络(二)(pytorch)
优化算法1-梯度下降法
import numpy sa np
import torch
from torchvision.datasets import MNIST #导入pytorch内置的mnist数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
%matplotlib inline
def data_tf(x):
x = np.array(x,dtype='float32') / 255 #将数据变到0 ~ 1 之间
x = (x - 0.5) / 0.5 #标准化
x = x.reshape((-1,))
x = torch.from_numpy(x)
return x
trai_set = MNIST('./data',train=True,transform=data_tf,download=True)#载入数据集申明定义的数据变换
test_set = MNIST('./data',train=False,transform=data_tf,download=True)
#定义loss函数
criterion = nn.CrossEntropyLoss()随机梯度下降法:
从0开始写:
def sgd_update(parameters,lr):
for param in parameters:
param.data = param.data - lr * param.grad.data可以先把batch size设置为1
train_data = DataLoader(train_set,batch_size=1,shuffle=True)
#使用Sequential定义3层神经网络
net = nn.Sequential(
nn.Linear(784,200),
nn.ReLU(),
nn.Linear(200,10),
)
#开始训练
losses1 = []
idx = 0
start = time.time() #计时开始
for e in range(5):
train_loss = 0
for im,label in train_data:
im = Variable(im)
label = Variable(label)
#前向传播
net.zero_grad()
loss.backward()
sgd_update(net.parameters(),1e-2) #使用0.01的学习率
#记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses1.append(loss.data[0])
idx += 1
print('epoch:{},Train Loss:{:.6f}'.format(e,train_loss / len(train_data)))
end = time.time()#计时结束
print('使用时间::{:.5f}s'.format(end - start))x_axis = np.linspace(0,5,len(losses1),endpoint=True)
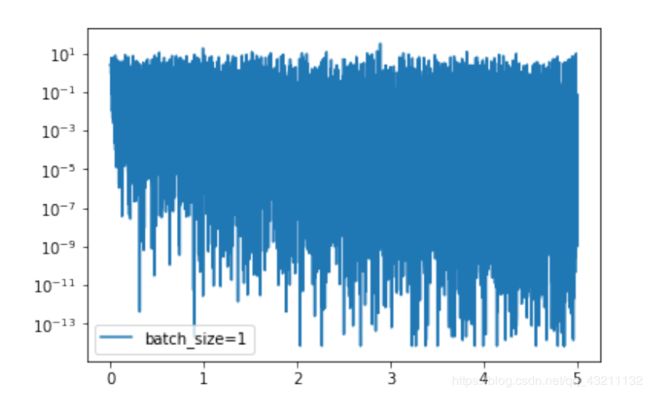
plt.semilogy(x_axis,losses1,label='batch_size=1')
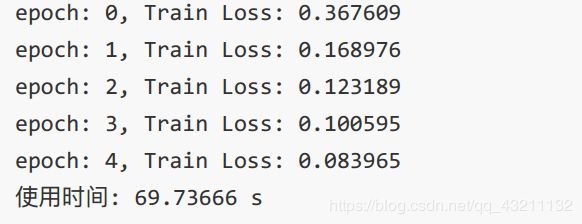
plt.legend(loc='best')可以看出,loss在剧烈震荡,因为每次都是只对一个样本点做计算,每一层的梯度都具有很高的随机性,而且需要耗费了大量的时间。
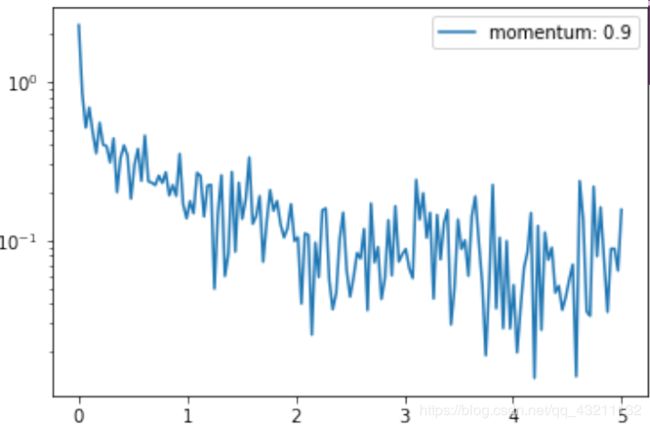
优化算法2-动量法
公式:
vi是当前速度,r是动量参数,是一个小于1的整数,后面的参数是学习率。
def sgd_momentum(parameters,vs,lr,garam):
for param,v in zip(parameters,vs):
v[:] = garam * v + lr * param.grad.data
param.data = param.data - vimport numpy sa np
import torch
from torchvision.datasets import MNIST #导入pytorch内置的mnist数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
%matplotlib inline
def data_tf(x):
x = np.array(x,dtype='float32') / 255 #将数据变到0 ~ 1 之间
x = (x - 0.5) / 0.5 #标准化
x = x.reshape((-1,))
x = torch.from_numpy(x)
return x
trai_set = MNIST('./data',train=True,transform=data_tf,download=True)#载入数据集申明定义的数据变换
test_set = MNIST('./data',train=False,transform=data_tf,download=True)
#定义loss函数
criterion = nn.CrossEntropyLoss()train_data = DataLoader(train_set,batch_size=1,shuffle=True)
#使用Sequential定义3层神经网络
net = nn.Sequential(
nn.Linear(784,200),
nn.ReLU(),
nn.Linear(200,10),
)
#将速度初始化和参数形状相同的零张量
vs = []
for param in net.parameters():
vs.append(torch.zeros_like(param.data))
#或者直接用自带的
#optimizer = torch.optim.SGD(net.parameters(),lr=1e-2,momentum=0.9)#加动量
#开始训练
losses1 = []
start = time.time() #计时开始
for e in range(5):
train_loss = 0
for im,label in train_data:
im = Variable(im)
label = Variable(label)
#前向传播
net.zero_grad()
loss.backward()
sgd_update(net.parameters(),1e-2) #使用0.01的学习率
#记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses1.append(loss.data[0])
idx += 1
print('epoch:{},Train Loss:{:.6f}'.format(e,train_loss / len(train_data)))
end = time.time()#计时结束
print('使用时间::{:.5f}s'.format(end - start))
加完动量之后loss能下降非常快,但一定要小心学习率和动量参数,这两个值会直接影响到每次更新的幅度,所以可以多事几个值。
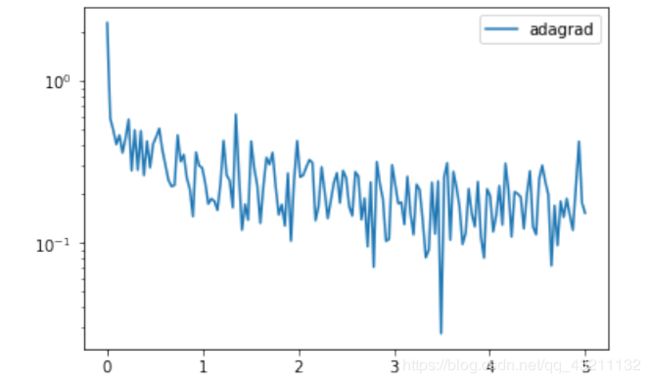
优化算法3-Adagrad
def sgd_adagrad(parameters,sqrt,lr):
eps = 1e-10
for param,sqr in zip(parameters,sqrt):
sqr[:] = sqr + param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - divimport numpy sa np
import torch
from torchvision.datasets import MNIST #导入pytorch内置的mnist数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
%matplotlib inline
def data_tf(x):
x = np.array(x,dtype='float32') / 255 #将数据变到0 ~ 1 之间
x = (x - 0.5) / 0.5 #标准化
x = x.reshape((-1,))
x = torch.from_numpy(x)
return x
trai_set = MNIST('./data',train=True,transform=data_tf,download=True)#载入数据集申明定义的数据变换
test_set = MNIST('./data',train=False,transform=data_tf,download=True)
#定义loss函数
criterion = nn.CrossEntropyLoss()train_data = DataLoader(train_set,batch_size=1,shuffle=True)
#使用Sequential定义3层神经网络
net = nn.Sequential(
nn.Linear(784,200),
nn.ReLU(),
nn.Linear(200,10),
)
#初始化梯度平方项
sqrt = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
#开始训练
losses = []
idx = 0
start = time.time() #计时开始
for e in range(5):
train_loss = 0
for im,label in train_data:
im = Variable(im)
label = Variable(label)
#前向传播
net.zero_grad()
loss.backward()
sgd_update(net.parameters(),1e-2) #使用0.01的学习率
#记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses1.append(loss.data[0])
idx += 1
print('epoch:{},Train Loss:{:.6f}'.format(e,train_loss / len(train_data)))
end = time.time()#计时结束
print('使用时间::{:.5f}s'.format(end - start))
优化算法4-RMSProp
def rmsprop(parameters,sqrs,lr,alpha):
eps = 1e-10
for param,sqr in zip(parameters,aqrs):
sqr[;] = alpha * sqr + (1 - alpha) * param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div替换:
#初始化梯度平方项
sqrs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))优化算法6-Adam
Adam是一个结合了动量法和RMSProp的优化算法,其结合了两者的优点。
def adam(parameters,vs,sqrs,lr,t,beta1=0.9,bata2=0.999):
eps = 1e-8
for param,v,sqr in zip(parameters,vs,sqrs):
v[:] = lata1 * v + (1 - beta1) * param.grad.data
sqr[:] = beta2 * sqr + (1 - beta2) * param.grad.data ** 2
v_hat = v / (1 - beta1 ** t)
s_hat = sqr / (1 - beta2 ** t)
param.data = param.data - lr * v_hat / torch.sqrt(s_hat + eps)替换:
#初始化梯度平方项和动量项
sqrs = []
vs = []
for param in net.paremeters():
sqrs.append(torch.zeros_like(param.data))
vs.append(torch.zeros_like(param.data))
t = 1