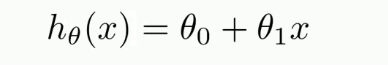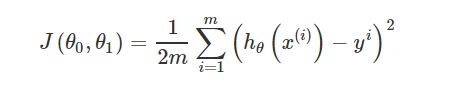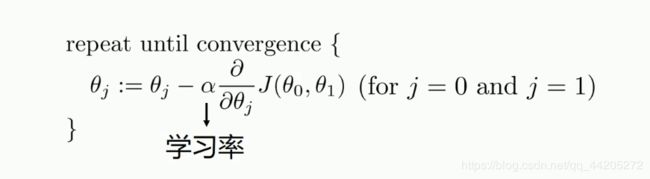线性回归以及非线性回归

一元线性回归

只含有一个自变量，对应的方程是一条直线

代价函数（损失函数）

• 这个代价函数也称为平方误差代价函数
• 思想：对于训练样本（x, y）来说，选择θ0，θ1 使h(x) 接近y
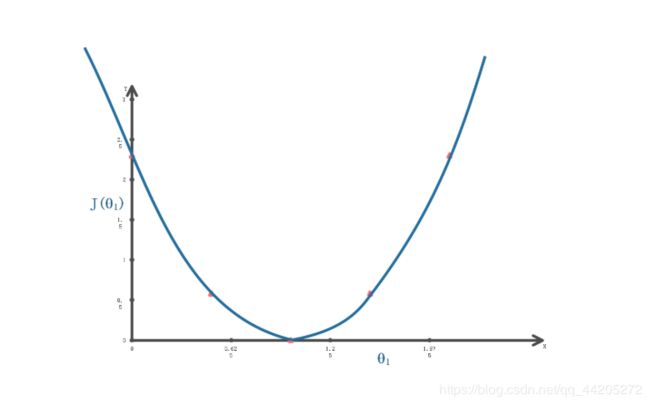
• 选择合适的（θ0, θ1）使得代价函数最小
• 每一个不同θ1的对应一条直线，我们的目的是找出最合适的θ1（最适合的直线）

梯度下降法

其实就是求导的过程

学习率不能太大也不能太小

梯度下降法的作用：最小化一个损失函数

 %matplotlib inline
import matplotlib.pyplot as plt
from sklearn import linear_model        #表示可以调用sklearn中的linear_model模块进行线性回归。
import numpy as np
# 下面两行代码用于显示中文
plt.rcParams['font.sans-serif']="Microsoft YaHei"
plt.rcParams['axes.unicode_minus']=False


def runplt(size=None):
    plt.figure(figsize=size)
    plt.axis([0, 25, 0, 25])
    plt.grid(True)
    return plt
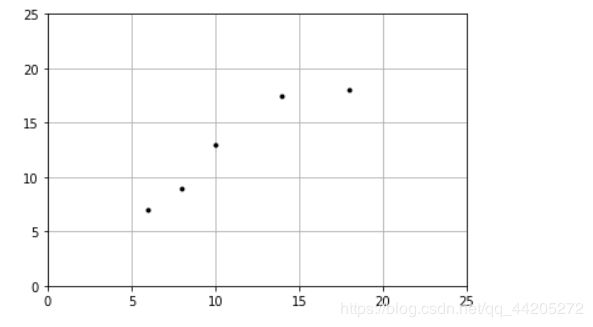
plt = runplt()
X = [[6], [8], [10], [14], [18]]
y = [[7], [9], [13], [17.5], [18]]
plt.plot(X, y, 'k.')
plt.show()


model = linear_model.LinearRegression()   # 建立线性回归模型
model.fit(X, y)    # 建模
display(model.intercept_)  #截距
display(model.coef_)  #线性模型的系数
a = model.predict([[12]])
# a[0][0]
print("{:.2f}".format(model.predict([[12]])[0][0]))

'''
array([1.96551724])

array([[0.9762931]])

13.68

'''

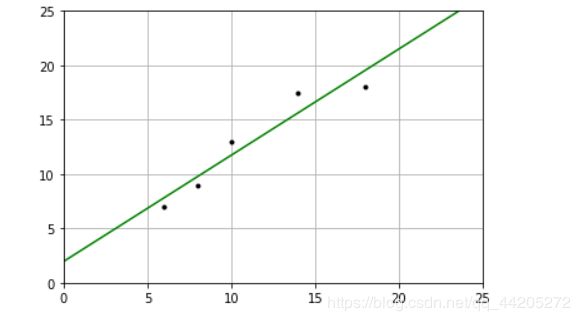
plt = runplt()
plt.plot(X, y, 'k.')
X2 = [[0], [10], [14], [25]]
model = linear_model.LinearRegression()
model.fit(X,y)
y2 = model.predict(X2)
plt.plot(X2, y2, 'g-')
plt.show()

多元线性回归

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import linear_model
# 下面两行代码用于显示中文
plt.rcParams['font.sans-serif']="Microsoft YaHei"
plt.rcParams['axes.unicode_minus']=False

# 导入数据
data = pd.read_excel("D:/数据/运输.xlsx")
data = data.values  # 转化成列表类型

# 切分数据
x_data = data[:,:-1]
y_data = data[:,-1]

# 创建模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)

print("系数>>>",model.coef_)
print("截距>>>",model.intercept_)

# 测试
x_test = [[102, 4]]
predict = model.predict(x_test)
print("预测>>>",predict)

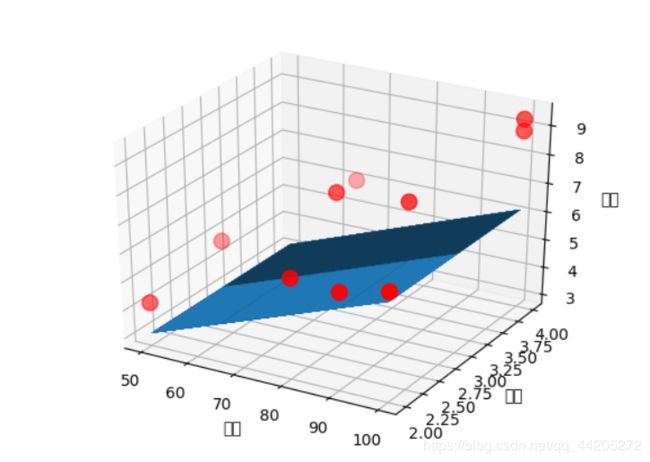
# 画出3D图像
ax = plt.figure().add_subplot(111, projection="3d")
ax.scatter(x_data[:,0], x_data[:,1],y_data,c='r', marker='o', s=100)
x0 = x_data[:,0]
x1 = x_data[:,1]
# 生成网格矩阵
x0, x1 = np.meshgrid(x0, x1)
z = model.intercept_ + x0*model.coef_[0] + model.coef_[1]
# 画3d图
ax.plot_surface(x0, x1, z)
ax.set_xlabel("里程")
ax.set_ylabel("次数")
ax.set_zlabel("时间")

plt.show()

特征缩放和交叉验证法

特征缩放

数据归一化

数据归一化就是把数据的取值范围处理为（0-1）或者（-1-1）之间

任意数据转化为0-1之间
newvalue = (oldvalue-min)/(max-min )

任意数据转化为-1-1之间
newvalue = ((oldvalue-main)/(max-min)-0.5)*2

均值标准化

newvalue = (oldvalue-平均值)/方差

交叉验证法

交叉验证是在机器学习建立模型和验证模型参数时常用的办法。交叉验证，顾名思义，就是重复的使用数据，把得到的样本数据进行切分，组合为不同的训练集和测试集，用训练集来训练模型，用测试集来评估模型预测的好坏。在此基础上可以得到多组不同的训练集和测试集，某次训练集中的某样本在下次可能成为测试集中的样本，即所谓“交叉”

那么什么时候才需要交叉验证呢？交叉验证用在数据不是很充足的时候。比如在我日常项目里面，对于普通适中问题，如果数据样本量小于一万条，我们就会采用交叉验证来训练优化选择模型。如果样本大于一万条的话，我们一般随机的把数据分成三份，一份为训练集（Training Set），一份为验证集（Validation Set），最后一份为测试集（Test Set）。用训练集来训练模型，用验证集来评估模型预测的好坏和选择模型及其对应的参数。把最终得到的模型再用于测试集，最终决定使用哪个模型以及对应参数

第一种是简单交叉验证，所谓的简单，是和其他交叉验证方法相对而言的。首先，我们随机的将样本数据分为两部分（比如： 70%的训练集，30%的测试集），然后用训练集来训练模型，在测试集上验证模型及参数。接着，我们再把样本打乱，重新选择训练集和测试集，继续训练数据和检验模型。最后我们选择损失函数评估最优的模型和参数。

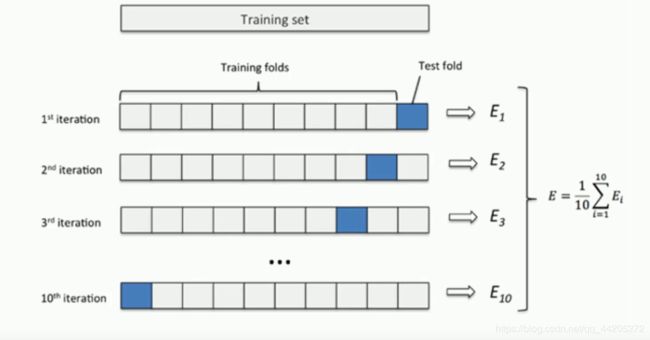
第二种是S折交叉验证（S-Folder Cross Validation）。和第一种方法不同，S折交叉验证会把样本数据随机的分成S份，每次随机的选择S-1份作为训练集，剩下的1份做测试集。当这一轮完成后，重新随机选择S-1份来训练数据。若干轮（小于S）之后，选择损失函数评估最优的模型和参数。

第三种是留一交叉验证（Leave-one-out Cross Validation），它是第二种情况的特例，此时S等于样本数N，这样对于N个样本，每次选择N-1个样本来训练数据，留一个样本来验证模型预测的好坏。此方法主要用于样本量非常少的情况，比如对于普通适中问题，N小于50时，我一般采用留一交叉验证。