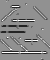Line Detection

http://homepages.inf.ed.ac.uk/rbf/HIPR2/linedet.htm

Line Detection

Common Names: Line detection

Brief Description

While edges (i.e. boundaries between regions with relatively distinct graylevels) are by far the most common type of discontinuity in an image, instances of thin lines in an image occur frequently enough that it is useful to have a separate mechanism for detecting them. Here we present a convolution based technique which produces an image description of the thin lines in an input image. Note that the Hough transform can be used to detect lines; however, in that case, the output is a parametric description of the lines in an image.

How It Works

The line detection operator consists of a convolution kernel tuned to detect the presence of lines of a particular width n, at a particular orientation . Figure 1 shows a collection of four such kernels, which each respond to lines of single pixel width at the particular orientation shown.

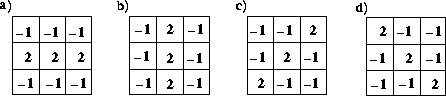
Figure 1 Four line detection kernels which respond maximally to horizontal, vertical and oblique (+45 and - 45 degree) single pixel wide lines.

These masks above are tuned for light lines against a dark background, and would give a big negative response to dark lines against a light background. If you are only interested in detecting dark lines against a light background, then you should negate the mask values. Alternatively, you might be interested in either kind of line, in which case, you could take the absolute value of the convolution output. In the discussion and examples below, we will use the kernels above without an absolute value.

If  denotes the response of kernel i, we can apply each of these kernels across an image, and for any particular point, if  for all  that point is more likely to contain a line whose orientation (and width) corresponds to that of kernel i. One usually thresholds  to eliminate weak lines corresponding to edges and other features with intensity gradients which have a different scale than the desired line width. In order to find complete lines, one must join together line fragments, e.g., with an edge tracking operator.

Guidelines for Use

To illustrate line detection, we start with the artificial image

which contains thick line segments running horizontally, vertically and obliquely across the image. The result of applying the line detection operator, using the horizontal convolution kernel shown in Figure 1.a, is

(Note that this gradient image has been normalized for display.) There are two points of interest to note here.

1. Notice that, because of way that the oblique lines (and some `vertical' ends of the horizontal bars) are represented on a square pixel grid, e.g.

   

   shows a zoomed region containing both features, the horizontal line detector responds to more than high spatial intensity horizontal line-like features, e.g.

   

2. On an image such as this one, where the lines to be detected are wider than the kernel (i.e. the image lines are five pixels wide, while the kernel is tuned for a single width pixel), the line detector acts like an edge detector: the edges of the lines are found, rather than the lines themselves.

This latter fact might cause us to naively think that the image which gave rise to

contained a series of parallel lines rather than single thick ones. However, if we compare this result to that obtained by applying the line detection kernel to an image containing lines of a single pixel width, we find some consistent differences. For example, we can skeletonize the original

(so as to obtain a representation of the original wherein most lines are a single pixel width), apply the horizontal line detector

and then threshold the result

If we then threshold the original line detected image at the same pixel value, we obtain the null image

Thus, the  values corresponding to the true, single pixel lines found in the skeletonized version are stronger than those  values corresponding to edges. Also, if we examine a cropped and zoomed version of the line detected raw image

and the skeletonized line detected image

we see that the single pixel width lines are distinguished by a region of minimal response on either side of the maximal response values coincident with the pixel location of a line. One can use this signature to distinguish lines from edges.

The results of line detecting (and then normalizing) the skeletonized version of this image with single pixel width convolution kernels of different  are

for a vertical kernel,

for the oblique 45 degree line, and

for the oblique 135 degree line. The thresholded versions are

and

respectively. We can add these together to produce a reasonably faithful binary representation of the line locations

It is instructive to compare the two operators under more realistic circumstances, e.g. with the natural image

After converting this to a grayscale image

and applying the Canny operator, we obtain

Applying the line detector yields

We can improve this result by using a trick employed by the Canny operator. By smoothing the image before line detecting, we obtain the cleaner result

However, even with this preprocessing, the line detector still gives a poor result compared to the edge detector. This is true because there are few single pixel width lines in this image, and therefore the detector is responding to the other high spatial frequency image features (i.e. edges, thick lines and noise). (Note that in the previous example, the image contained the feature that the kernel was tuned for and therefore we were able to threshold away the weaker kernel response to edges.) We could improve this result by increasing the width of the kernel or geometrically scaling the image.

Interactive Experimentation

You can interactively experiment with this operator by clicking here.

Exercises

1. Consider the basic image

   

   We can investigate the scale of features in the image by applying line detection kernels of different widths. For example, after convolving with a single pixel horizontal line detecting kernel we discover that only the striped shirt of the bank robber contains single pixel width lines. The normalized result is shown in

   

   and after thresholding (at a value of 254), we obtain

   

   a) Perform the same analysis on the image

   

   using different width kernels to extract the different features (e.g. roof, windows, doors, etc.). Threshold your result so that the final images contain a binary description of just the feature of interest. b) Try your kernels on other architectural drawings such as

   

   and

   

2. Investigate a line detection algorithm which might extract the tail feathers of the peacock in

   

   You will most likely need to apply some smoothing as a first step and you may then want apply several different kernels and add the results together. Compare your final result with an edge detection algorithm, e.g. Roberts cross,Sobel, Compass and/or Canny edge detector.

References

D. Vernon Machine Vision, Prentice-Hall, 1991, Chap. 5.

R. Gonzalez and R. Woods Digital Image Processing, Addison-Wesley Publishing Company, 1992, pp 415 - 416.