深度之眼Pytorch打卡（三）：Pytorch张量操作（包括torch.stack()理解、广播(broadcastable)的理解）

前言

---

   张量的操作主要包括张量的形状改变和张量的计算，前者包括张量的拼接（包括torch.stack()理解）、拆分、索引和变换等，后者包括加法、减法，乘加、除加等。本笔记的框架主要来源于深度之眼，并作了一些相关的拓展，拓展内容主要源自对torch文档的翻译和理解。

   文中涉及张量创建函数的使用方法见：深度之眼Pytorch打卡（二）：Pytorch张量与张量的创建

---

张量拼接

---

• torch.cat()——catenate（拼接）

torch.cat(tensors, dim=0, out=None)

   tensors: 张量用()或[]括起来，张量的dtype要相同才能进行拼接。
   dim: 要拼接的维度。以二维张量为例，dim = 0表示第0个维度上进行拼接，要求其他维度（第1维度）尺寸相同。 dim = 1表示第1个维度上进行拼接，要求其他维度（第0维度）尺寸相同。
   代码：
    a、b的第``0维度不同，第1维度相同，故可以在第0维度上（行）进行拼接，却不能在第1维度上（列）进行拼接。

import torch
a = torch.randn(2, 3)
b = torch.ones(1, 3)
print(a, b)
c = torch.cat((a, b), dim=0)
print(c)

   结果：
   维度0尺寸变成3，维度1不变。

tensor([[-1.6062, -0.3639, -0.1687],
        [-1.6002, -1.2058, -1.3905]]) 
tensor([[1., 1., 1.]])
tensor([[-1.6062, -0.3639, -0.1687],
        [-1.6002, -1.2058, -1.3905],
        [ 1.0000,  1.0000,  1.0000]])

   代码：
   a,b两个张量的第1维不同，第0和2维相同，因此只能在第1个维度上进行p拼接。

import torch
a = torch.randn(2, 2, 3)
b = torch.ones(2, 1, 3)
print(a, '\n', b)
c = torch.cat((a, b), dim=1)
print(c)

   结果：
   第1个维度尺寸变成了3，其他维度没有变。

tensor([[[ 1.2217,  0.2418, -0.5646],
         [-0.6613,  0.9546,  1.2515]],

        [[ 0.5315,  1.3444,  0.3384],
         [-0.3015,  0.4637,  0.7923]]]) 
 tensor([[[1., 1., 1.]],

        [[1., 1., 1.]]])
tensor([[[ 1.2217,  0.2418, -0.5646],
         [-0.6613,  0.9546,  1.2515],
         [ 1.0000,  1.0000,  1.0000]],

        [[ 0.5315,  1.3444,  0.3384],
         [-0.3015,  0.4637,  0.7923],
         [ 1.0000,  1.0000,  1.0000]]])

• torch.stack()

torch.stack(tensors, dim=0, out=None)

   dim: 该函数会新建一个维度，并在该维度上进行拼接，注意与torch.cat()区别。如两个二维的张量拼接，该函数会在第三维上进行拼接。
   代码：
   dim可以取0，1和2，分别表示在0，1和2三个维度上创建一个新维度，并在该维度上实现张量的拼接。

a = torch.ones([2, 3], dtype=torch.int64)
b = torch.randint(2, 18, size=(2, 3))
print(a, '\n', b)
c = torch.stack([a, b], dim=0)
d = torch.stack([a, b], dim=1)
e = torch.stack([a, b], dim=2)
print('dim = 0:', c, c.shape, ' \n', 'dim = 1:', d, d.shape, '\n', 'dim = 2:', e, e.shape)

   结果：
   假设两个2x3 的二维张量拼接。

tensor([[1, 1, 1],
        [1, 1, 1]]) 
 tensor([[15, 13, 10],
        [12, 10,  9]])
dim = 0: tensor([[[ 1,  1,  1],
         [ 1,  1,  1]],

        [[15, 13, 10],
         [12, 10,  9]]]) torch.Size([2, 2, 3])  
 dim = 1: tensor([[[ 1,  1,  1],
         [15, 13, 10]],

        [[ 1,  1,  1],
         [12, 10,  9]]]) torch.Size([2, 2, 3]) 
 dim = 2: tensor([[[ 1, 15],
         [ 1, 13],
         [ 1, 10]],

        [[ 1, 12],
         [ 1, 10],
         [ 1,  9]]]) torch.Size([2, 3, 2])

   dim = 0： 新建一个0维度，并在该维度上进行拼接，该维度的尺寸等于张量个数。拼接后，原先2x3二维张量的0维度，变成新张量的1维度，原先二维张量的1维度，变成新张量的2维度。那么拼接完成将构成一个2x 2x3的三维张量，注意与cat区别。

   dim = 1： 新建一个1维度，并在该维度上进行拼接，该维度的尺寸等于张量个数。原先2x3二维张量的0维度，变成新张量的0维度，原先二维张量的1维度，变成新张量的2维度。那么原来两个张量中第0维的第一个的元素（代码中分别是：[1, 1, 1]和[15, 13, 10]）应当出现在新张量的第0维的第一个元素中，原来两个张量中第0维的第二个的元素（代码中分别是：[1, 1, 1]和[12, 10, 9]）应当出现在新张量的第0维的第二个元素中。直观理解就是，将原先两个2x3张量的第一行的元素取出来，拼成一个新的2x3的张量，然后将原先两个2x3张量的第二行的元素取出来，拼成另一个新的2x3的张量，然后再将新的两个2x3的张量在维度0上堆成一个三维张量，完成也将构成一个2x 2x3的三维张量。

   dim = 2： 新建一个2维度，并在该维度上进行拼接，该维度的尺寸等于张量个数。原先2x3二维张量的0维度，变成新张量的0维度，原先二维张量的1维度，变成新张量的1维度，容易得到拼接完成的三维张量尺寸为2x 3x2。由于很抽象，现在把此三维张量当成一个放了2个二维张量一维张量。那么原来两个2x3张量的第一行第一列的元素（代码中分别是：1和15）应当出现在三维张量中的第一个二维张量的第一行，即[ 1, 15]。原来两个2x3张量的第二行第一列的元素（代码中分别是：1和12）应当出现在三维张量中的第二个二维张量的第一行，即[ 1, 12]，以此类推就可以得到最后拼接的结果。

   如果都把三维张量当成一个放了2个二维张量一维张量，那么dim=0，增加的维度是类似索引的东西，原先的行列都不变，就好像是直接堆积起来的。dim=1增加的维度是行，原先的行变成了索引，原先的列还是列，那么原先第一个张量的第一行元素，就变成了三维张量中第一个二维张量的第一行元素，原先第二个张量的第一行元素，就变成了三维张量中第一个二维张量的第二行元素，以此类推。dim=1增加的维度是列，原先的行变成了索引，原先的列变成了行，都发生了变化。

---

张量拆分

---

• torch.chunk()

torch.chunk(input, chunks, dim=0) 

   chunks: 将input在给定的dim上切分成chunks等份，如果原张量在dim上的尺寸不能被chunks整除，那么切分出来的前n-1个张量，在该dim上的尺寸等于商的向上取整，第n个，也就是最后一个，则取剩余的尺寸。
   代码：

a = torch.full([3, 5], 2)
b = torch.chunk(a, 2, dim=0)
c = torch.chunk(a, 2, dim=1)
print(a, '\n', b, '\n', c)

   结果：
   在第0维上分成两份，第一份的尺寸为3/2=1.5向上取整，即为2，最后一份尺寸为3-2=1。另一个维度上类似。

tensor([[2., 2., 2., 2., 2.],
        [2., 2., 2., 2., 2.],
        [2., 2., 2., 2., 2.]]) 
        
(tensor([[2., 2., 2., 2., 2.],
        [2., 2., 2., 2., 2.]]), tensor([[2., 2., 2., 2., 2.]]))  
        
(tensor([[2., 2., 2.],
        [2., 2., 2.],
        [2., 2., 2.]]), tensor([[2., 2.],
        [2., 2.],
        [2., 2.]]))

• torch.split()

torch.split(tensor, split_size_or_sections, dim=0)

   split_size_or_sections： 可以为一个整数值，也可以为一个列表。为整数值时，表示将原张量在给定维度dim上，以split_size_or_sections为尺寸，切分；如果原张量在dim上的尺寸不能被split_size_or_sections整除，那么较小的那个尺寸，留到最后一个张量。如果split_size_or_sections是一个列表，则在dim上，分别以该列表中的值为尺寸，依次切分出对应张量；注意，列表中所有值的和应和原张量在该维度dim上的尺寸相同。
   代码：

a = torch.eye(4, 3)
b = torch.split(a, 2, dim=1)
c = torch.split(a, [1, 2, 1], dim=0)
print(a, b, c)

   结果：
   4x3的张量，在1维度上以2为大小切分，可以切分成两份，由于不能整除，故最后一个张量在0维度上尺寸为1。列表为[1,2,3]表示切分成三份，大小分别是，1,2,3,。

tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.],
        [0., 0., 0.]])
        
(tensor([[1., 0.],
        [0., 1.],
        [0., 0.],
        [0., 0.]]), tensor([[0.],
        [0.],
        [1.],
        [0.]]))
        
(tensor([[1., 0., 0.]]), tensor([[0., 1., 0.],
        [0., 0., 1.]]), tensor([[0., 0., 0.]]))

---

张量索引

---

• torch.masked_select()

torch.masked_select(input, mask, out=None)

   mask: mask是一个布尔类似的张量，即其中的值非False即Ture，mask和input的形状可以不匹配。函数返回的是一个一维的张量，值就是在mask为1时对应的input中的值，即通过mask中为Ture的元素来进行索引和筛选。
   代码：
   a.ge(4)表示a中大于等于4的地方为Ture，其余为False。a.le表示小于等于，a.lt表示小于,a.gt表示小于。

   代码：

a = torch.normal(4, 2, (3, 3))
mask = a.ge(4)
c = torch.masked_select(a, mask)
print(a, '\n', 'mask:', mask, '\n', c)

   结果：

tensor([[1.3276, 3.2400, 7.4209],
        [2.3469, 3.4026, 6.6096],
        [0.9894, 6.1387, 5.2828]]) 
 mask: tensor([[False, False,  True],
        [False, False,  True],
        [False,  True,  True]]) 
 tensor([7.4209, 6.6096, 6.1387, 5.2828])

• torch.index_select()

torch.index_select(input, dim, index, out=None) 

   index: 在维度dim上，通过index来索引数据并返回，并将返回的数据组成一个新张量。index是一个长整型的一维张量，里面存的就是序号。
   代码：

a = torch.rand(3, 4)
index = torch.tensor([1., 2.], dtype=torch.int64)
b = torch.index_select(a, 0, index)
c = torch.index_select(a, 1, index)
print(a, '\n', 'dim=0', b, '\n', 'dim=1', c)

   结果：
   分别索引第2,3行和第2,3列的数据，返回并构成一个新的张量。

tensor([[0.0227, 0.4536, 0.8596, 0.1714],
        [0.7133, 0.6720, 0.6465, 0.9513],
        [0.9363, 0.8257, 0.0443, 0.6123]]) 
 dim=0 tensor([[0.7133, 0.6720, 0.6465, 0.9513],
        [0.9363, 0.8257, 0.0443, 0.6123]]) 
 dim=1 tensor([[0.4536, 0.8596],
        [0.6720, 0.6465],
        [0.8257, 0.0443]])

---

张量变换

---

• torch.reshape()

torch.reshape(input, shape)

   shape: 要输出张量的形状，注意shape中的元素个数应该与input中的元素总数相同。如果shape中有一维为-1，表示该维的尺寸有其他维和input决定。可以用某一维为-1的方法，把一个二维张量转换成一维行张量或者一维列张量。
   代码：

a = torch.rand(2, 4)
b = torch.reshape(a, [-1, 1])
c = torch.reshape(a, [1, -1])
d = torch.reshape(a, [2, 2, 2])
print(a, 'id1：', id(a), '\n', b, 'id2：', id(b),'\n', c, 'id3：', id(c), '\n', d, 'id4：', id(d),)

  结果：
  将原先的2x4二维张量，分别变换成了8x1、1x8和2x2x2三种形状，无论怎么变元素总数要保证相同。观察id1与id2发现两者是共享内存的（多运行几次，发现有时相同有时不太），解释是：当张量在内存中是连续时，新张量与input共享内存，笔者不是很明白。

tensor([[0.2386, 0.5697, 0.6933, 0.9063],
        [0.1332, 0.1767, 0.8973, 0.4874]]) id1： 2402252272968 
        
 tensor([[0.2386],
        [0.5697],
        [0.6933],
        [0.9063],
        [0.1332],
        [0.1767],
        [0.8973],
        [0.4874]]) id2： 2402249282968 
        
 tensor([[0.2386, 0.5697, 0.6933, 0.9063, 0.1332, 0.1767, 0.8973, 0.4874]]) id3： 2402456457112 
 
 tensor([[[0.2386, 0.5697],
         [0.6933, 0.9063]],

        [[0.1332, 0.1767],
         [0.8973, 0.4874]]]) id4： 2402471105064

• torch.squeeze() ——squeeze（挤压）

torch.squeeze(input, dim=None, out=None)

   dim:dim为默认值时，该函数会对所有维度进行压缩，即把所有维度中长度为1的维度都去掉。dim为某一维度时，只压缩该维度，即如果该维度长度为1那么该维度会被去掉，如果该维度的长度大于1，那么没有什么影响。
  代码：

a = torch.empty(1, 2, 3, 1, 1)
b = torch.squeeze(a)
c = torch.squeeze(a, dim=0)
d = torch.squeeze(a, dim=2)
e = torch.unsqueeze(b, dim=0)
print(a.shape, b.shape, c.shape, d.shape, e.shape)

  结果：
  没有规定dim的时候，所以维度都被压缩，结果是三个长度为1的维度都被去掉了。当规定dim的时候，就只压缩给定维度。torch.unsqueeze(input, dim)作用相反，必须指定维度。

torch.Size([1, 2, 3, 1, 1]) 
torch.Size([2, 3]) 
torch.Size([2, 3, 1, 1]) 
torch.Size([1, 2, 3, 1, 1]) 
torch.Size([1, 2, 3])

• torch.transpose()

torch.transpose(input, dim0, dim1)

  函数实现input的两个维度的交换，当input是一个二维张量时，就相当于是矩阵转置，即行列互换.其实，矩阵转置可以用函数torch.t(input)简洁实现。
  代码：

a = torch.rand(3, 2, 2)
b = torch.transpose(a, 0, 1)
c = torch.transpose(b, 1, 2)
print(a, b, c)

  结果：常在彩色图像预处理的时候，将通道数x长x宽转变成长x宽x通道数。可以用在torch.stack()中的那种理解方式来理解这个函数。

tensor([[[0.9307, 0.6331],
         [0.2420, 0.6447]],

        [[0.7714, 0.6065],
         [0.9144, 0.3039]],

        [[0.6839, 0.9605],
         [0.0999, 0.3407]]]) 
         
tensor([[[0.9307, 0.6331],
         [0.7714, 0.6065],
         [0.6839, 0.9605]],

        [[0.2420, 0.6447],
         [0.9144, 0.3039],
         [0.0999, 0.3407]]]) 

tensor([[[0.9307, 0.7714, 0.6839],
         [0.6331, 0.6065, 0.9605]],

        [[0.2420, 0.9144, 0.0999],
         [0.6447, 0.3039, 0.3407]]])

---

张量运算

---

• torch.add()

torch.add(input, alpha=1, other, out=None)

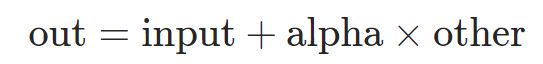
 alpha： 系数，为一数值。张量other的每个元素，与标量alpha相乘，并将结果加到张量input的每个元素中，其中other与input要么是相同形状的，要么是可广播的（broadcastable），最终要实现的是对应元素操作。返回结果为张量。
 broadcastable： 广播的目的是将两个不同形状的张量，变成两个形状相同的张量两个张量。标量与任何张量都是可广播的，即标量可以通过重复自身以构成任何形状的张量。 当两个张量维度都不为零时，从后往前对比两个张量的各个维度，要么两个张量该维度的尺寸相同，要么有个张量该维度尺寸为1或者不存在，原文：When iterating over the dimension sizes, starting at the trailing dimension, the dimension sizes must either be equal, one of them is 1, or one of them does not exist。如尺寸为(2, 4, 2)和(2, 1, 2)的两个张量是可以广播的，尺寸为(2, 4, 2)和(4, 2)的两个张量也是可以广播的，它们都符合上述规定，前者在1维度上重复4次(1,2)的张量就可以构成(2, 4, 2)，后者在0维上重复2次(4,2)就可以构成(2, 4, 2)。

  代码：

a = torch.rand(2, 4, 2)
b = torch.rand(2, 1, 2)
c = torch.add(a, 10, b)
print(a, '\n', b, '\n', c)

  结果：c = a + 10*b

tensor([[[0.5733, 0.0105],
         [0.5275, 0.9351],
         [0.6544, 0.5832],
         [0.3372, 0.7443]],

        [[0.6654, 0.7294],
         [0.8054, 0.5487],
         [0.5223, 0.3010],
         [0.0125, 0.7512]]]) 
 tensor([[[0.4775, 0.6785]],

        [[0.0302, 0.6722]]]) 
 tensor([[[5.3485, 6.7953],
         [5.3028, 7.7199],
         [5.4297, 7.3680],
         [5.1125, 7.5291]],

        [[0.9675, 7.4509],
         [1.1075, 7.2703],
         [0.8244, 7.0225],
         [0.3146, 7.4727]]])

• torch.addcdiv()

torch.addcdiv(input, value=1, tensor1, tensor2, out=None)

  value: 系数，为一数值。在做优化的时候常用到上述表达式，此时的value便是学习率lr，而商便是梯度。input,tensor1, tensor2的形状也必须可以广播。

• torch.addcmul()

torch.addcmul(input, value=1, tensor1, tensor2, out=None)

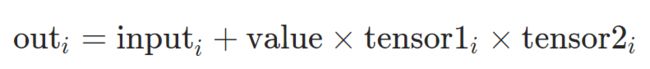
input,tensor1, tensor2的形状也必须可以广播。

  张量数学运算中比较常用的就是以上三个函数了，其他的还有三角函数、指数、对数、分段函数、绝对值函数、逻辑运算和一些误差计算函数，在pytorch的文档里都有详细列出，需要时查一下就ok。

# 四则运算
torch.div(input, other, out=None) 
torch.mul(input, other, out=None)
# 三角函数
torch.angle(input, out=None)  # 复数转换成弧度
torch.asin(input, out=None)   # 反正弦，得弧度
torch.atan(input, out=None)   # 反正切，不考虑象限，得弧度
torch.atan2(input,other,out = None )# 考虑象限的反正切，得弧度。
torch.cos(input, out=None)
torch.cosh(input, out=None)  # 双曲余弦
torch.sin(input, out=None) 
torch.sinh(input, out=None) 
torch.tan(input, out=None)
torch.tanh(input, out=None) 

# 逻辑运算
torch.bitwise_not（input,out = None) # 按位非
torch.bitwise_xor(input, other, out=None) # 按位亦或
torch.logical_not(input, out=None) # 输出布尔类型
torch.logical_xor(input, other, out=None)

# 取整运算
torch.ceil(input, out=None) # 向上取整
torch.floor(input, out=None) # 向下取整
torch.round(input, out=None) # 最近整数
# 分段函数
torch.clamp(input, min, max, out=None) # 将数据限制在min与max之间

# 误差函数
torch.erf(input, out=None)  # 高斯误差函数
torch.erfc(input, out=None) #互补误差函数，等于1-erf
# 指数函数
torch.exp(input, out=None)
torch.expm1(input, out=None) #exp-1
# 对数函数
torch.log(input, out=None) 
torch.log10(input, out=None) 
torch.log1p(input, out=None) # ln(1+x)
torch.log2(input, out=None)
# 幂函数
torch.pow(input, exponent, out=None) 
torch.sqrt(input, out=None) # 平方根
torch.rsqrt(input, out=None) # 平方根的倒数
torch.reciprocal(input, out=None) # 取倒数
# 取相反数，即乘以-1
torch.neg(input, out=None)
# 复数
torch.real(input, out=None) # 取实部
# 激活函数
torch.sigmoid(input, out=None) 
torch.tanh(input, out=None) 
# 符号函数
torch.sign(input, out=None)

---

参考

---

  https://www.cnblogs.com/Assist/p/11158028.html
  https://pytorch.org/docs/stable/torch.html