cs231n作业:assignment1 - knn
title: cs231n作业:assignment1 - knn
id: cs231n-1h-1
tags:
- cs231n
- homework
categories: - AI
- Deep Learning
date: 2018-09-26 12:41:15
GitHub地址:https://github.com/ZJUFangzh/cs231n
个人博客:fangzh.top
使用KNN算法来完成图像识别,数据集用的是cifar10。
首先看一下数据集的维度
# Load the raw CIFAR-10 data.
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
可以看到,每一张图片是 32 × 32 × 3 32×32×3 32×32×3,训练集有50000张,测试集有10000张
Training data shape: (50000, 32, 32, 3)
Training labels shape: (50000,)
Test data shape: (10000, 32, 32, 3)
Test labels shape: (10000,)
为了更够更快的计算,就选5000张做训练,500张做测试就好了
# Subsample the data for more efficient code execution in this exercise
num_training = 5000
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]
而后把像素拉成3072的行向量
# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)
因为knn不需要训练,所以先存入数据:
from cs231n.classifiers import KNearestNeighbor
# Create a kNN classifier instance.
# Remember that training a kNN classifier is a noop:
# the Classifier simply remembers the data and does no further processing
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
然后要修改k_nearest_neighbor.py中的compute_distances_two_loops
这里套了两层循环,也就是比较训练集和测试集的每一张图片的间距:
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in xrange(num_test):
for j in xrange(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension. #
#####################################################################
dists[i][j] = np.sqrt(np.sum(np.square(X[i,:] - self.X_train[j,:])))
#####################################################################
# END OF YOUR CODE #
#####################################################################
return dists
得到了一个 ( 500 , 5000 ) (500,5000) (500,5000)的dists矩阵。
然后修改predict_labels函数
def predict_labels(self, dists, k=1):
"""
Given a matrix of distances between test points and training points,
predict a label for each test point.
Inputs:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
gives the distance betwen the ith test point and the jth training point.
Returns:
- y: A numpy array of shape (num_test,) containing predicted labels for the
test data, where y[i] is the predicted label for the test point X[i].
"""
num_test = dists.shape[0]
y_pred = np.zeros(num_test)
for i in xrange(num_test):
# A list of length k storing the labels of the k nearest neighbors to
# the ith test point.
closest_y = []
#########################################################################
# TODO: #
# Use the distance matrix to find the k nearest neighbors of the ith #
# testing point, and use self.y_train to find the labels of these #
# neighbors. Store these labels in closest_y. #
# Hint: Look up the function numpy.argsort. #
#########################################################################
#找到每一个测试图片中对应的5000张训练集图片,距离最近的前k个
closest_y = self.y_train[np.argsort(dists[i])[:k]]
#########################################################################
# TODO: #
# Now that you have found the labels of the k nearest neighbors, you #
# need to find the most common label in the list closest_y of labels. #
# Store this label in y_pred[i]. Break ties by choosing the smaller #
# label. #
#########################################################################
#然后将这K个图片进行投票,得票数最多的就是预测值
y_pred[i] = np.argmax(np.bincount(closest_y))
#########################################################################
# END OF YOUR CODE #
#########################################################################
return y_pred
预测一下:
# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)
# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
结果是0.274
再试试k=5的结果,是0.278
然后再修改compute_distances_one_loop函数,这次争取只用一个循环
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in xrange(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
#######################################################################
#利用python的广播,一次性算出每一张图片与5000张图片的距离
dists[i, :] = np.sqrt(np.sum(np.square(self.X_train - X[i, :]),axis=1))
#######################################################################
# END OF YOUR CODE #
#######################################################################
return dists
验证一下间距是
Difference was: 0.000000
Good! The distance matrices are the same
然后争取不用循环compute_distances_no_loops,这一步比较难,想法是利用平方差公式 ( x − y ) 2 = x 2 + y 2 − 2 x y (x-y)^2 = x^2 + y^2 - 2xy (x−y)2=x2+y2−2xy,使用矩阵乘法和二次广播,直接算出距离,注意矩阵的维度
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy. #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
temp_2xy = np.dot(X,self.X_train.T) * (-2)
temp_x2 = np.sum(np.square(X),axis=1,keepdims=True)
temp_y2 = np.sum(np.square(self.X_train),axis=1)
dists = temp_x2 + temp_2xy + temp_y2
dists = np.sqrt(dists)
#########################################################################
# END OF YOUR CODE #
#########################################################################
return dists
对比一下三种方法的时间,我这里不知道为什么two比one短,理论上是循环越少时间越短:
Two loop version took 24.510484 seconds
One loop version took 56.412211 seconds
No loop version took 0.183508 seconds
交叉验证
用交叉验证来找到最好的k
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
X_train_folds = np.array_split(X_train, num_folds)
y_train_folds = np.array_split(y_train, num_folds)
################################################################################
# END OF YOUR CODE #
################################################################################
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
classifier = KNearestNeighbor()
for k in k_choices:
accuracies = []
for fold in range(num_folds):
temp_X = X_train_folds[:]
temp_y = y_train_folds[:]
X_val_fold = temp_X.pop(fold)
y_val_fold = temp_y.pop(fold)
temp_X = np.array([y for x in temp_X for y in x])
temp_y = np.array([y for x in temp_y for y in x])
classifier.train(temp_X,temp_y)
y_val_pred = classifier.predict(X_val_fold,k=k)
num_correct = np.sum(y_val_fold == y_val_pred)
accuracies.append(num_correct / y_val_fold.shape[0])
k_to_accuracies[k] = accuracies
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))
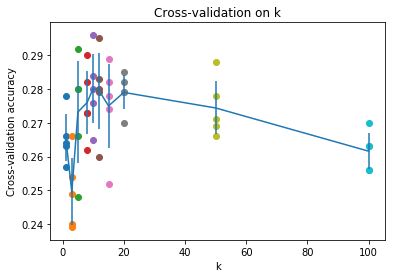
画个图:
# plot the raw observations
for k in k_choices:
accuracies = k_to_accuracies[k]
plt.scatter([k] * len(accuracies), accuracies)
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()
# Based on the cross-validation results above, choose the best value for k,
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)
# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))
得到最好的k=10,准确率是0.282
小结
- cs231n的作业比DeepLearning.ai的难多了,不是一个档次的,关键是提示比较少,所以自己做起来比较费劲
- 主要要学会向量化的运算,少用loop循环
- knn已经被淘汰了,这个作业只是让我们入门看看图像识别大概怎么做