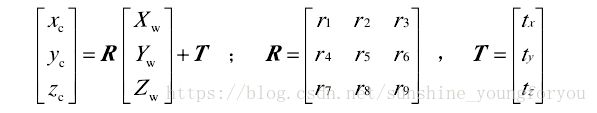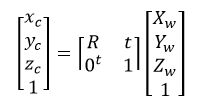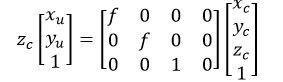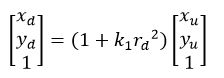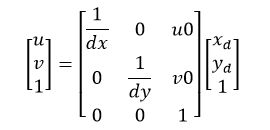OpenCV双目视距之相机标定原理(1)
一:什么是标定
摄像机的标定即确定摄像机的内外部参数的过程。
摄像机内部参数是由摄像机内部几何和光学特性决定的,主要包括焦距f和主点坐标(
u
0
,
v
0 ),还有镜头畸变的各类畸变系数等。
摄像机外部参数是指摄像机坐标系相对世界坐标的位置关系,包括旋转矩阵R和平移向量t。
二:标定模型介绍
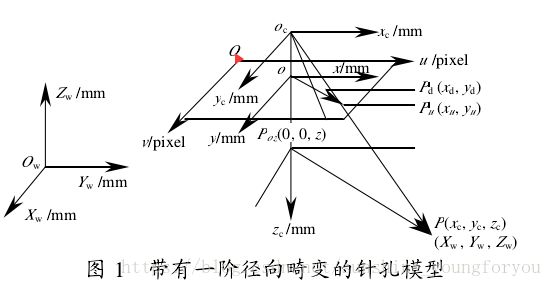
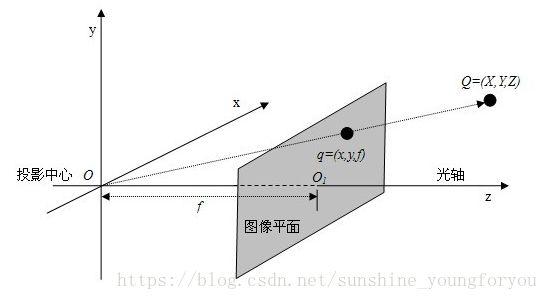
如图1为带有一阶径向畸变的针孔模型,模型中有四个坐标系:
1.计算机图像坐标系Ouv(也称像素坐标系),
原点O位于CCD图像平面的左上角,u和v分别表示像素位于数组的列数和行数。
2.图像平面坐标系oxy,
原点(即主点)定义在摄像机光轴与图像平面的交点,一般为图像平面的中心,x,y轴分别与u,v轴平行。Pu (xu , yu )表示针孔模型在P点的理想图像坐标,
Pd (xd , yd )是由透镜径向畸变引起的偏离Pu (xu ,yu )的实际坐标。
3.摄像机坐标系OcXcYcZc,
原点Oc定义在摄像机的光心,Xc,Yc轴分别平行于x,y轴,Zc轴与光轴重合。o
co为摄像机的有效焦距f,(Xc,Yc,Zc)表示物点P在摄像机坐标系下的三维坐标。
4.世界坐标系OwXwYwZw,
根据具体环境来定。(Xw,Yw,Zw)表示物点P在世界坐标系下的三维坐标。
世界坐标系和相机坐标系是三维空间 ,而其他两个是二维平面
三:标定中四个坐标系的变换过程
从世界坐标系到计算机图像坐标系的变换可以分成如下4步:
(1)世界坐标系与摄像机坐标系的变换
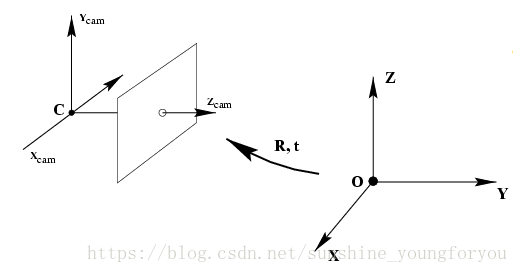
这一步是三维点到三维点的转换,示意图如下:
可以用旋转矩阵R和平移向量T来描述:
也即:
(2)针孔模型下的理想透视投影变换
即从摄像机坐标系到理想图像坐标系的变换:
示意图如下:
点Q(X,Y,Z)【对应图一的物点P(Xc,Yc,Zc) 】为摄像机坐标系空间中的一点,该点被光线投影到图像平面上的q(x,y,f)点【对应图一中的Pu (xu , yu ) 】 。
图像平面与光轴z轴垂直,和投影中心距离为f (f是相机的焦距)。
按照三角比例关系可以得出:
x/f = X/Z y/f = Y/Z 。也即:
矩阵形式表现为:
以上将坐标为(X,Y,Z)的P点映射到投影平面上坐标为(x,y)的Pu点的过程称作
投影变换。
(3)理想图像坐标系与实际图像坐标系的转换
考虑一阶径向畸变,建立畸变模型为:
矩阵形式表示为:
式中rd的平方等于xd的平方加上yd的平方,k1为一阶径向畸变系数。
(4)实际图像坐标系到计算机图像坐标系的转换
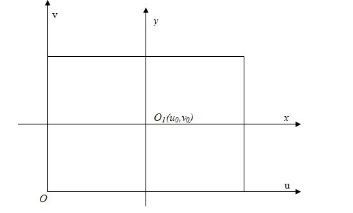
像平面坐标系和像素坐标系虽然在同一个平面上,但是原点并不是同一个。
以图像平面的左上角或左下角为原点建立坐标系。假设像平面坐标系原点位于图像左下角,水平向右为u轴,垂直向上为v轴,均以像素为单位。
以像平面与光轴的交点O1 为原点建立坐标系,水平向右为x轴,垂直向上为y轴。原点O1一般位于图像中心处,O1在以像素为单位的图像坐标系中的坐标为(u0, v0),( u0,v0)即为主点坐标。
示意图如下:
设每个像素的物理尺寸大小为 dx * dy (mm) ( 由于单个像素点投影在图像平面上是矩形而不是正方形,因此可能dx != dy),
图像平面上某点在成像平面坐标系中的坐标为(
xd, yd),在像素坐标系中的坐标为(
u, v),则二者满足如下关系:
矩阵形式表现为:
式中(u0,v0)为主点o的像素坐标,即主点坐标,(dx,dy)分别为图像平面上x,y方向上单位像素间的距离。
sx为两者之比,即图像纵横比。
而如何由图像坐标系中的点的信息求得物点在世界坐标系中的点的信息可以归纳为如下:
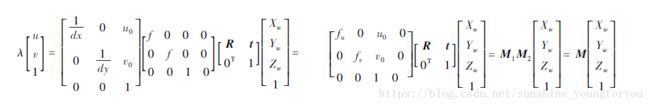
其中,
λ是一个比例因子;
( u,v,1)为点P在图像坐标系中投影的齐次坐标;
dx、dy为每个像素在x轴和y轴方向上的物理尺寸;
(Xw,Yw,Zw,1)为P点在世界坐标系下的坐标;
fu =f /dx、fv = f /dy,分别代表u轴和v轴的尺度因子;
M1由fu、fv、u0、v0决定,称为内部参数;
M2由摄像机相对于世界坐标系的方位决定,称为摄像机的外部参数;
M称为投影矩阵;
四:参考文献资料
《基于平行双目立体视觉的测距系统_刘盼》
《高精度双目CCD测距研究_申琳》
《基于共面点的摄像机线性标定法_邹凤娇》
https://www.cnblogs.com/Jessica-jie/p/6596450.html
https://blog.csdn.net/honyniu/article/details/51004397