先进非线性控制方法 INDI 快速部署到PX4用于四旋翼控制(part2)
目录
- 一、PX4 v11 的姿态控制解析
- 1. 角度环控制
- 2. 角速度环控制
- 3. 控制分配
- 二、简易INDI如何部署到PX4
- 1. 获取角加速度 和 电机转速测量值
- (1)角加速度
- (2)转速
- 2. 具体实现过程
- (0)简要回顾与分析
- (1)获取角加速度
- (2)获取指令微分
- (3)修改控制律公式
- (4)获取 M c 0 M_{c_{\tiny 0}} Mc0
- 结语
一、PX4 v11 的姿态控制解析
这一部分主要介绍PX4核心控制算法是怎么实现的。其实核心的控制算法部分很简单,大部分代码都是在进行各种分情况讨论,各种安全检查。下面简单介绍一下,希望大家看了之后有点收获,能给我点个赞,嘿嘿。
1. 角度环控制
这部分代码在 src/modules/mc_att_control里
主程序在 mc_att_control_main.cpp 里
简单介绍就是先生成姿态角指令(roll, pitch, yaw的指令,即attitude_setpoint)

姿态指令生成(在函数最后publish了)
然后根据这个指令计算姿态角速度指令(即_rates_sp)
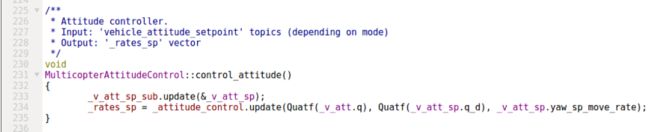
计算姿态角速度指令(_attitude_control是AttitudeControl类的实例,具体实现在同文件夹下的AttitudeControl里)
2. 角速度环控制
这部分代码在 src/modules/mc_rate_control里
即根据姿态角速度指令来计算得到期望力矩,这也是本文需要改的部分。
主程序在 MulticopterRateControl.cpp 里
简单介绍就是先订阅 角速度指令rates_sp 的消息
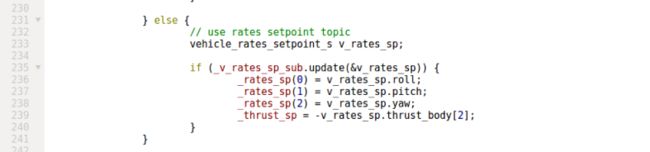
获取角速度指令
然后计算控制力矩指令
![]()
根据当前的角速度和角速度指令计算控制力矩指令(就是这个att_control)
接着发布这个att_control

发布控制力矩指令att_control
3. 控制分配
这部分内容也挺多的,主要是在 src/lib下的 mixer 和 mixer_module里,四旋翼的具体实现是在src/lib/mixer/MultirotorMixer/MultirotorMixer.cpp 里
直接看分配的主要函数:mix
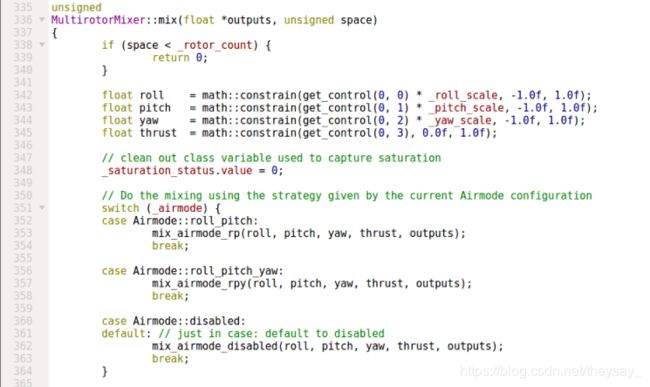
多旋翼分配实现
其实就是先获取控制力矩指令,然后分情况调用函数进行分配。
比如在使用jmavsim仿真时调用的是 mix_airmode_disabled 函数

mix_airmode_disabled中分配的实现
这部分就是具体的实现过程了,首先是先不考虑 yaw 进行分配,然后最后再单独分配 yaw.
二、简易INDI如何部署到PX4
1. 获取角加速度 和 电机转速测量值
经过 part1 的推导之后我们知道,INDI需要得到角加速度的值来进行计算,猜怎么着?我惊奇的发现 PX4 v11 里这个角加速度值已经算出来了,之前的版本里都是没有这个量的,而且这个角加速度的量在现在的 PX4 里也没有用到,不知道他们是要搞什么。
(1)角加速度
接下来讲一讲这个角加速度的始末:
这个角加速度怎么来的呢?
在src/modules/sensors/vehicle_angular_velocity是用来计算角速度和角加速度的,其中的.cpp 文件里有计算的流程
简单来说就是:
获取陀螺仪数据并矫正热误差
→ 矫正运行中的偏差
→ 应用陷波滤波器对上面得到的角速度值原始值进行滤波
→ 对滤波后的角速度进行微分得到角加速度值
→ 把角速度和角加速度存一下
→ 对两个值应用低通滤波器进行平滑处理
处理完了就把两个量发布
于是我们就可以在msg里找到 vehicle_angular_velocity.msg 和 vehicle_angular_acceleration.msg 这两个文件了,也就是说可以通过 μORB 订阅到这两个topic了。另外,这个 vehicle_angular_acceleration.msg 目前还没有存到日志文件里,可以通过简单处理把他存到日志文件里,便于后面的分析。
(2)转速
经过 part1 的推导之后我们知道,INDI需要得到 电机转速 的值来进行计算,猜怎么着?我惊奇的发现 PX4 v11 里这个电机转速值已经估计出来了,之前的版本里都是没有这个量的,而且这个电机转速的量在现在的 PX4 里也没有用到,不知道他们是要搞什么。(他们不会要把姿态控制换成INDI吧。。)
这个电机转速测量值(估计值)我是先在msg文件夹下发现的,就是 rpm.msg 。但是这个东西我还妹有完全搞明白,不知道是根据什么估算的电机转速,有兴趣的朋友可以了解一下px4里这个 rpm 是怎么估计的。(我知道有的穿越机电调可以回传电机转速,这个就比较成熟了。还有篇文章是用类似鼠标里那个光栅编码器来测转速的,不过这个可能撞一下就坏了,不太好)
但是!要说但是了。
我试了下,这个转速估计值在jmavsim仿真里是没有的计算出来的,没试gazebo。
另外,用这个电机转速还有个问题在于,px4里实际输出的电机指令也不是电机的转速,而是分配之后,到每个电机头上的归一化的(可以认为是推力)值计算出的 pwm 值,所以考虑电机转速回传之后,会带来很多麻烦,我嫌麻烦还没有分析这个,所以暂且按下不表。
于是我的处理方法是,用类似的滞后环节去模拟电机的响应过程。也就是对电机进行建模,然后估计电机的当前转速。目前的简易做法是计算出力矩指令之后,加上一个滞后作为实际得到的控制力矩
2. 具体实现过程
(0)简要回顾与分析
INDI 的原理在 part1 中已经介绍过,下面简要回顾并分析下需要修改的地方:
对于角速度控制环来说,令指令跟踪误差为 e Ω = Ω − Ω r e_{\tiny \Omega}=\Omega-\Omega_r eΩ=Ω−Ωr
则角速度跟踪误差的动态方程可以写成
e ˙ Ω = Ω ˙ 0 − Ω ˙ r + g ( x s t a t e s ) Δ ω 2 \dot{e}_{\Omega}=\dot{\Omega}_{\tiny 0}-\dot{\Omega}_r+g(x_{states})\Delta{\omega^2} e˙Ω=Ω˙0−Ω˙r+g(xstates)Δω2
那么根据 INDI 的原理可以得到(电机引起的)力矩的增量
G M Δ ω 2 = − J ( Ω ˙ 0 − Ω ˙ r + K p e Ω ) G_M\Delta{\omega^2}=-J(\dot{\Omega}_{\tiny 0}-\dot{\Omega}_r+K_pe_{\tiny \Omega}) GMΔω2=−J(Ω˙0−Ω˙r+KpeΩ)
然后可以得到力矩的指令:
M c = G M ⋅ ω 0 2 + G M ⋅ Δ ω 2 M_c=G_M\cdot{\omega_{\tiny 0}^2}+G_M\cdot\Delta{\omega^2} Mc=GM⋅ω02+GM⋅Δω2
其中 ω 0 2 \omega_{\tiny 0}^2 ω02是估计出来的或者测量回来的转速。
或者写成 M c = M c 0 + G M ⋅ Δ ω 2 M_c=M_{c_{\tiny 0}}+G_M\cdot\Delta{\omega^2} Mc=Mc0+GM⋅Δω2
其中 M c 0 M_{c_{\tiny 0}} Mc0是计算或者估计出来的当前控制力矩
也就是说,需要改的或者添加的就是 (1)获取角加速度,(2)获取指令微分,(3)修改控制律公式,(4)获取 M c 0 M_{c_{\tiny 0}} Mc0。( (2)可选,因为这个东西我看有的控制方法里用,有的不用,比如在PID的误差 e e e 微分里就包含这个指令微分,但是如果用测量值 y y y 计算微分量的话就不包含这个指令微分)
需要修改的代码都在 src/modules/mc_rate_control/Multicopter
(1)获取角加速度
角加速度已经发布了,所以直接订阅就行了
怎么订阅,有个简单的方法,直接按照角速度订阅的方式来一遍就行了:
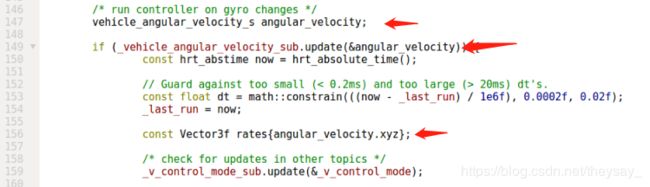
订阅角速度,照例订阅一下角加速度即可
(2)获取指令微分
直接对订阅得到的 rates_sp 进行微分即可,不过这一步我省略了…
(3)修改控制律公式
角速率环的控制律公式在src/modules/mc_ate_control/RateControl/RateControl.cpp里,就一行:

角速度PID控制律
这是经典的PID控制,这里我们如果要改成INDI只需要:
![]()
角度环INDI控制律
这两个式子就是在实现
G M Δ ω 2 = − J ( Ω ˙ 0 + K p e Ω ) G_M\Delta{\omega^2}=-J(\dot{\Omega}_{\tiny 0}+K_pe_{\tiny \Omega}) GMΔω2=−J(Ω˙0+KpeΩ)
和 M c = M c 0 + G M ⋅ Δ ω 2 M_c=M_{c_{\tiny 0}}+G_M\cdot\Delta{\omega^2} Mc=Mc0+GM⋅Δω2
( e Ω e_{\tiny \Omega} eΩ的符号不对是因为我的误差的定义和PX4正好相反)
另外解释下,其中我在yaw通道加了个微分误差factor,因为仿真的时候发现yaw通道老震荡,所以多加了微分项抑制一下。按理说是不需要微分项的,后面可能要看一下为什么会出现震荡情况。
另外,在本文中这个 G M Δ ω 2 = − J ( Ω ˙ 0 + K p e Ω ) G_M\Delta{\omega^2}=-J(\dot{\Omega}_{\tiny 0}+K_pe_{\tiny \Omega}) GMΔω2=−J(Ω˙0+KpeΩ)公式里的 J J J就相当于一个可整定的参数。原因有四点:(1)我这里没有修改Mixer里的 G M G_M GM,(2)操纵导数本来就比较难获得(需要螺旋桨的力系数和力矩系数),(3)INDI里的操纵导数本来就是一个可以用来整定的量,(4)操纵力矩分配之后映射到的是输出给电机的PWM信号,而PWM信号和电机转速之间的关系也是个黑箱
(4)获取 M c 0 M_{c_{\tiny 0}} Mc0
M c 0 M_{c_{\tiny 0}} Mc0 也就是上面 角度环INDI控制律 图里的torque_prev.
这里我是直接用一个低通滤波器作为控制力矩响应模型的。
意思就是说,真实的控制力矩响应比控制力矩指令就差了一个低通滤波器过程。即:
M c 0 = M c ⋅ G l p f M_{c_{\tiny 0}}=M_{c}\cdot{G_{lpf}} Mc0=Mc⋅Glpf
实现起来就是这么一句:
torque_prev = _lp_filters_rate.apply(torque1);
由于懒,我这里用的 filter 还是px4自带的low pass filter。
!!!!!这里需要注意的一点是:由于之前获取角加速度的时候,也用了低通滤波器和陷波滤波器,导致角加速度与当前的真实角加速度有滞后,所以为了让测量或者估计的真实力矩响应与角速度同步,需要在测量或者估计的真实力矩上 再 加上同样的滞后。
OK,这四部分就介绍完了,剩下的就是调调参数的事情。我大概调了半天,才调到和之前的 PID 效果差不多的样子。
结语
目前我改的这个 PX4 v11 不是一个稳定的版本,是开发中的版本(很神奇地在里面发现了角加速度估计值和电机转速估计值,不知道开发人员是在憋什么大招)。但是要修改其他版本其实也是大同小异,毕竟v11里只是把角速度控制单独拿出来放到一个文件夹下了而已。
INDI的好处是鲁棒性和容错性比较强,在模型失配程度比较高的情况下也可以得到比较好的控制效果,另外在出现故障或者外部扰动的时候也能快速恢复稳定。这实际上得益于INDI能够实时将系统动态通过角加速度反馈到控制器中,比如当外部有强风吹的时候,PID需要有积分项才能重新实现在强风影响下的稳定,相当于是一个对强风影响的估计,这个过程是比较慢的,但是反馈角加速度可以快速把这个影响反馈到控制器中。大概就是这个意思,如果要深入理解可能要结合仿真比较好。
就介绍到这里,如果大家看了之后有什么想法,欢迎交流。


