YOLO算法的调整与优化

一. 代码篇

1.1 引入const引用形参改善代码效率

举个栗子：
在convolutional_layer.c文件的convolutional_out_height函数中：

/*
**  根据输入图像的高度(h)，两边补0的个数(pad)，卷积核尺寸(size)以及跨度(stride)计算输出的特征图的高度
**  输入：l    卷积层，包含该卷积层的所有参数，实际这里没有必要输入整个l，因为只需要到其中的四个参数而已
**  输出：int类型，输出图像的高度
**  说明：这个函数的实现应该可以进一步改善一下，虽然这个函数只是在最初构建网络时调用一次，之后就不调用了，不怎么影响性能，
**       但输入整个l实在不妥（l比较大，按值传递复制过程比较冗长），要么就只输入用到的四个参数，要么传入l的指针，
**       并且不需要返回值了，直接在函数内部为l.out_h赋值
*/
int convolutional_out_height(convolutional_layer l)

若改成：

int convolutional_out_height(const convolutional_layer &l)
是否更加合理？

1.2 指针释放空间后最好做置0处理

举个栗子：
在文件layer.c中的void free_layer(layer l)函数中

void free_layer(layer l)
{
...
    if (l.indexes)        free(l.indexes);
    **l.indexes = NULL;**
    if (l.rand)           free(l.rand);
    **l.rand = NULL;**
    if (l.cost)           free(l.cost);
    **l.cost = NULL;**
    if (l.biases)         free(l.biases);
    **l.biases = NULL;**
    if (l.weights)        free(l.weights);
    **l.weights = NULL;**
...
}

1.3 使用strncmp而不是strcmp

举个栗子：

/*  return (strcmp(s->type, "[net]") == 0
        || strcmp(s->type, "[network]") == 0);*/
   return (strncmp(s->type, "[net]", strlen("[net]")) == 0
        || strncmp(s->type, "[network]", strlen("[network]")) == 0);

二. 算法加速篇

2.1 引入定点数的优化

关于定点数的理论知识，可以参考我的博客：

定点数与浮点数

具体的定点数转换公式如下：
一般，取q=12

/* The basic operations performed on two numbers a and b of fixed point q
format returning the answer in q format */

#define FADD(a, b)     ((a) + (b))
#define FSUB(a, b)     ((a) - (b))
//#define FMUL(a, b, q)  (((a)*(b))>>(q))
#define FMUL(a, b, q)  ((long)((a)*(b))>>(q))
#define FDIV(a, b, q)  (((a)<<(q))/(b))


/* The basic operation where a is of fixed point q format and b is
an integer */

#define FADDI(a, b, q)  ((a) + ((b)<<(q)))
#define FSUBI(a, b, q) ((a) - ((b)<<(q)))
#define FMULI(a, b)    ((a)*(b))
#define FDIVI(a, b)    ((a)/(b))


/* convert a from q1 format to q2 format */

#define FCONV(a, q1, q2)  (((q2) > (q1)) ? (a)<<((q2)-(q1)) : (a)>>((q1) - (q2)))

/* the general operation between a in q1 format and b in q2 format
returning the result in q3 format */

#define FADDG(a, b, q1, q2, q3)  (FCONV(a, q1, q3) + FCONV(b, q2, q3))
#define FSUBG(a, b, q1, q2, q3)  (FCONV(a, q1, q3) - FCONV(b, q2, q3))
#define FMULG(a, b, q1, q2, q3)   FCONV((a)*(b), (q1)+(q2), q3)
#define FDIVG(a, b, q1, q2, q3)  (FCONV(a, q1, (q2) + (q3))/(b))


/* convert to and from floating point */
#define TOFIX(d, q)  ((int) ( (d)*(double) (1<<(q)) ))
#define TOFLT(a, q)  (  (double)(a) / (double)(1<<(q)) )

2.2 在参数矩阵中引入稀疏矩阵的存储方式

参考博客：稀疏矩阵存储格式总结+存储效率对比:COO,CSR,DIA,ELL,HYB

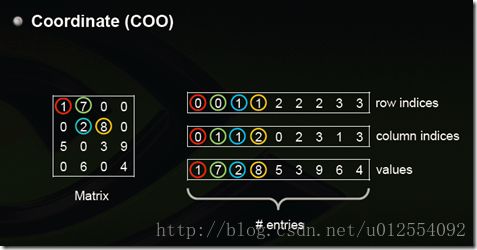
Coordinate（COO）

这是最简单的一种格式，每一个元素需要用一个三元组来表示，分别是（行号，列号，数值），对应上图右边的一列。这种方式简单，但是记录单信息多（行列），每个三元组自己可以定位，因此空间不是最优。

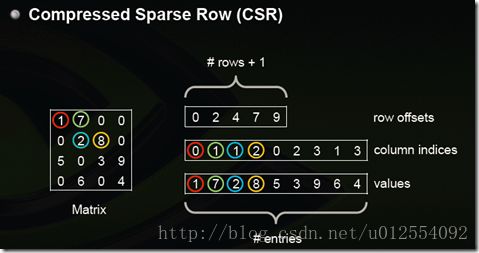
Compressed Sparse Row (CSR)

CSR是比较标准的一种，也需要三类数据来表达：数值，列号，以及行偏移。CSR不是三元组，而是整体的编码方式。数值和列号与COO一致，表示一个元素以及其列号，行偏移表示某一行的第一个元素在values里面的起始偏移位置。如上图中，第一行元素1是0偏移，第二行元素2是2偏移，第三行元素5是4偏移，第4行元素6是7偏移。在行偏移的最后补上矩阵总的元素个数，本例中是9。

CSC是和CSR相对应的一种方式，即按列压缩的意思。

ELLPACK (ELL)

用两个和原始矩阵相同行数的矩阵来存：第一个矩阵存的是列号，第二个矩阵存的是数值，行号就不存了，用自身所在的行来表示；这两个矩阵每一行都是从头开始放，如果没有元素了就用个标志比如*结束。上图中间矩阵有误，第三行应该是 0 2 3。

注：这样如果某一行很多元素，那么后面两个矩阵就会很胖，其他行结尾*很多，浪费。可以存成数组，比如上面两个矩阵就是：

0 1 * 1 2 * 0 2 3 * 1 3 *

1 7 * 2 8 * 5 3 9 * 6 4 *

但是这样要取一行就比较不方便了

Diagonal (DIA)

对角线存储法，按对角线方式存，列代表对角线，行代表行。省略全零的对角线。(从左下往右上开始：第一个对角线是零忽略，第二个对角线是5，6，第三个对角线是零忽略，第四个对角线是1，2，3，4，第五个对角线是7，8，9，第六第七个对角线忽略)。

这里行对应行，所以5和6是分别在第三行第四行的，前面补上无效元素*。如果对角线中间有0，存的时候也需要补0，所以如果原始矩阵就是一个对角性很好的矩阵那压缩率会非常高，比如下图，但是如果是随机的那效率会非常糟糕。

Hybrid (HYB) ELL + COO

为了解决ELL中提到的，如果某一行特别多，造成其他行的浪费，那么把这些多出来的元素（比如第三行的9，其他每一行最大都是2个元素）用COO单独存储。

typedef struct _unified_matrix     UM;
typedef struct _unified_matrix  _dense_matrix;
typedef _dense_matrix DM;
typedef struct _unified_matrix  _compressed_sparse_matrix;
typedef _compressed_sparse_matrix CSPM;

typedef struct _sparse_matrix     SPM;

typedef enum   FORMAT          FORMAT;

typedef enum FORMAT {
    DENSE,
    CSR,
    CSC
};

typedef struct  _unified_matrix
{
    FORMAT format;

    int rows;
    int cols;
    int bits_val;
    int num_vals;
    unsigned short *vals;
    unsigned  short *weight_powers;
    short int *weight_masks;

    int *row_offsets;
    int *col_offsets;
    int *starts;
    int bits_intv;
    int num_intvs;
    unsigned short *intvs;
};

typedef struct _sparse_matrix {
    FORMAT format;

    int rows;
    int cols;
    int *row_offsets;
    int *col_offsets;
    int num_vals;
    float *vals;
    int *INTvals;   //Mark
    int *offsets;
    unsigned char *powers;  //Mark

};