频率域图像增强及MATLAB实现
一、频域滤波知识梳理
频域滤波和空间域滤波可以视为对同一个图像增强问题的两种解决方式,二者殊途同归。在一些情况下,图像增强问题适合在频域中完成,另一些情况下,适合在空间域中完成,我们常常根据需要在二者之间做抉择,或是在二者之间相互转换,选择一个合适的方法来解决问题。
频域增强导图如下:
二.频域滤波基础
频域滤波必不可少的工具是 傅里叶变换。傅里叶变换提供了一种从空间域到频域的转换手段,且用傅里叶反变换可以实现从频域到空间域的无损转换,不丢失任何信息。
下面仅将频域滤波(二维图像)中用到的fft和ifft的实现附上,具体的傅里叶相关知识可查看另一篇博客:《傅里叶家族》。
2.1 二维快速傅里叶变换fft2
%% imgFft2
%{
函数: Y=fft2(X,m,n)
函数说明:计算二维快速傅里叶变换
参数说明: X:输入图像
m,n:为将X的第一和第二维规整到指定的长度,当m和n均为2的整数次幂时算法的执行速度要比m和n均为素数要快
返回值:Y是计算得到的傅里叶频谱,是一个复数矩阵
备注: abs(Y)可得到幅度谱
angle(Y)可得到相位谱
fftshift(X) 可将频谱图像零点移到中心位置
备注:此程序可帮助理解FFT后,幅度谱的意义%}clc; %清空命令行
clear;%清空变量
I1=imread('beauty.jpg');
subplot(1,2,1);
imshow(I1);
title('beauty.jpg');
I2=fft2(I1);%计算二维FFT
spectrum =fftshift(I2);%将零点移到中心
temp= log(1+ abs(spectrum) ); %对幅值做 对数变换 以压缩动态范围
subplot(1,2,2);
imshow(temp,[]);
title('FFT');
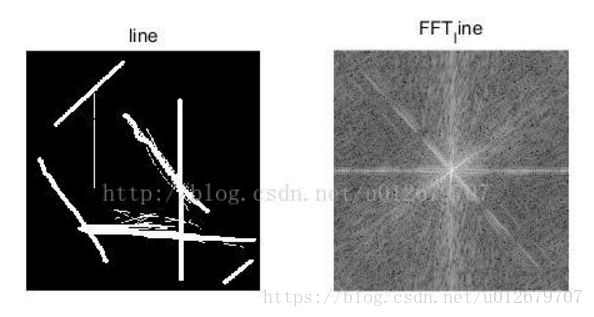
I1=imread('line.bmp');
figure,
subplot(1,2,1);
imshow(I1);
title('line');
I2=fft2(I1);%计算二维FFT
spectrum =fftshift(I2);%将零点移到中心
temp= log(1+ abs(spectrum) ); %对幅值做 对数变换 以压缩动态范围
subplot(1,2,2);
imshow(temp,[]);
title('FFT_line');处理结果分析:
1、横向比较。原图与经过FFT后的频谱图之间的关系,低频区实质图像中变化较缓慢的像素区,如变化不明显的背景区域;高频区指灰度变化较剧烈的像素区,如边缘和噪声等。
2、纵向比较。FFT后的图像以幅度谱显示,可看出图beauty与图line的幅度谱之间的差异。图beauty较为平滑,在其傅里叶频谱图FFT.jpg中,低频部分对应的幅值比较高,即低频分量占优势;而图line中的水平与竖直的线灰度变化更加剧烈,相应的频谱中高频分量较强(注意是与beauty图相比,高频区域更多一些,但整体还是低频区域更多,毕竟背景无变化的黑色区都属于低频嘛)。由此可知,FFT后的幅度谱,可以反映原图像中的灰度变化情况(即灰度变化是否剧烈)。
2.2 逆快速傅里叶变换 Ifft2
%% imgIfft2
%{
函数: Y=ifft2(X)
函数说明:逆二维快速傅里叶变换
参数说明:X:输入图像
m,n:将图像规整到m*n
返回值: 反变换后得到的原始图像备注:此程序为美女与猫--交换两幅图像的相位谱
%}
clc;
clear;
I1=imread('beauty.jpg');
I2=imread('CAT.jpg');
subplot(1,2,1);
imshow(I1);
title('beauty原图');
subplot(1,2,2);
imshow(I2);
title('CAT原图');
%计算二维FFT,得到频谱
F1=fft2(I1);
F2=fft2(I2);
%分别求幅度谱和相位谱
A1=abs(F1);
A2=abs(F2);
Phase1=angle(F1);
Phase2=angle(F2);
%交换相位谱并重建图像
New1=A1.*cos(Phase2) +A1.*sin(Phase2).*i;
New2=A2.*cos(Phase1) +A2.*sin(Phase1).*i;
%傅里叶反变换
New1=abs(ifft2(New1));
New2=abs(ifft2(New2));
figure,
subplot(1,2,1);
imshow(New1,[]);
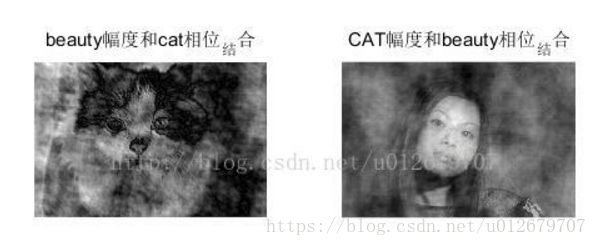
title('beauty幅度和cat相位_结合');
subplot(1,2,2);
imshow(New2,[]);
title('CAT幅度和beauty相位_结合');
结果分析:
1、通过此例程可以发现,两幅图经过相位交换后,图像的内容与相位谱所对应的图像一致,说明了相位谱决定图像的轮廓结构;
2、图像的明暗、灰度变化趋势等则取决于幅度谱,即幅度谱反映了图像整体上各个方向的频率分量的相对强度。
三、频域低通滤波
3.1 频域滤波器实现
此频域滤波器需结合 频域滤镜(ff)一起来实现具体的频域滤波功能。
%% imfreqfilt.m
%{
函数: function out=imfreqfilt(I,ff)
函数说明:频域滤波函数
参数说明:I:输入原图像(空间域图像)
ff:频域滤镜(大小与原图像相等)
返回值: 滤波后图像(空间域图像)
注意:
1、 输入的图像应为待处理的空域图像,输出值也为空域图像
2、 既然输入输出都为空域图像,那为何叫频域滤波?
答:频域滤波,是说滤波过程是在频域进行,但结果是经过IFFT反变换回空间域了,所以你看不到频域处理过程。
年轻人,要发现表象背后的机理啊哈哈哈
%}
function out=imfreqfilt(I,ff)
%若是RGB,需转换为Gray
if(ndims(I)==3 && (size(I,3)==3) ) %RGB图像 size(I,3)表示I的第三维分量大小,ndims(I)代表I的维数
I=rgb2fray(I);
end
%检查输入
if( size(I) ~=size(ff) ) % ‘~=’不等于号
msg1=sprintf('%s:滤镜与原图像不等大,请检查输入',mfilename); % mfilename: File name of currently running code
msg2=sprintf('%s:滤镜操作已经取消',mfilename);
eid=sprintf('Image:%s: ImgSizeNotEqual',mfilename);
error(eid,'%s %s',msg1,msg2);
end
%快速FFT
I1=fft2(I);
I1=fftshift(I1); % 将原点移动到频率中心
%应用滤镜及反变换
G=I1.*ff; % 对应元素相乘实现滤波。 频域相乘 I(u,v)H(u,v)
G=ifftshift(G); %将原点从频率中心移回原位
out=ifft2(G); % IFFT得空间域函数
%求幅度
out=abs(out);
%归一化以便显示
out=out/(max(out(:)) );3.2 理想低通滤波器
3.21 理想低通滤镜构建
% 频域低通滤波器 imidealflpf.m
%{
函数: function ff=imidealflpf(I,freq)
函数说明:构造理想的频域低通滤波器(即 滤镜)
参数说明:I:为输入原图像
freq:为截止频率
返回值: 与I等大的频域滤镜
%}
function ff=imidealflpf(I,freq)
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
if (sqrt ((i-M/2)^2+ (j-N/2)^2 ) >freq) ff(i,j)=0; %高于截止频率 设为0
end
end
end
% 理想低通滤波器应用 ideal_exe.m
I1=imread('baby.bmp');
I=imnoise(I1,'salt & pepper');
%生成滤镜 (截止频率为20)
ff=imidealflpf(I,20);
%应用滤镜,频域滤波
out=imfreqfilt(I,ff);
%生成滤镜 (截止频率为40)
ff1=imidealflpf(I,40);
%应用滤镜,频域滤波
out1=imfreqfilt(I,ff1);
%生成滤镜 (截止频率为60)
ff2=imidealflpf(I,60);
%应用滤镜,频域滤波
out2=imfreqfilt(I,ff2);
%显示空间域图像
subplot(1,4,1);
imshow(I);
title('原图');
subplot(1,4,2);
imshow(out);
title('f=20');
subplot(1,4,3);
imshow(out1);
title('f=40');
subplot(1,4,4);
imshow(out2);
title('f=60');
%显示频域图像(fft--fftshift--abs--log)
If=fft2(I);
If=fftshift(If);
If=abs(If); %幅度谱
If=log(1+If); %压缩范围
outf=fft2(out);
outf=fftshift(outf);
outf=abs(outf); %幅度谱
outf=log(1+outf); %压缩范围
out1f=fft2(out1);
out1f=fftshift(out1f);
out1f=abs(out1f); %幅度谱
out1f=log(1+out1f); %压缩范围
out2f=fft2(out2);
out2f=fftshift(out2f);
out2f=abs(out2f); %幅度谱
out2f=log(1+out2f); %压缩范围
figure,
subplot(1,4,1);
imshow(If,[]);
title('原图');
subplot(1,4,2);
imshow(outf,[]);
title('f=20');
subplot(1,4,3);
imshow(out1f,[]);
title('f=40');
subplot(1,4,4);
imshow(out2f,[]);
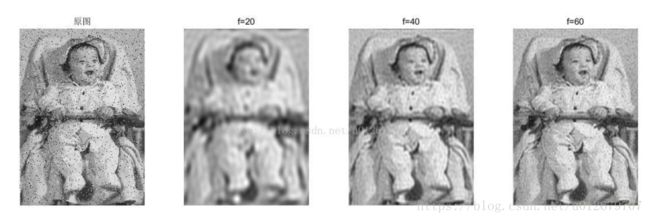
title('f=60');不同截止频率的滤波结果:
结果分析:
1、当截止频率非常低(f=20)时,只有非常靠近原点的低频成分才能通过,图像模糊较为严重;
2、当截止频率越高(f=40/60)时,通过的频率成分越多,图像模糊程度越小,所获得的图像越接近原图像;
3、可发现,理想低通滤波器并不能很好的兼顾 滤除噪声 与 保留细节 这两个方面,这和空域滤波中的平均平滑相似。
3.3 高斯低通滤波器
3.31 构造滤镜
%高斯低通滤波器滤镜 imgaussflpf.m
%{
函数: function ff=imgaussflpf(I,sigma)
函数说明:构造高斯低通滤镜
参数说明:I:输入图像
sigma:标准差
返回值:与原图像等大的高斯低通滤镜
%}
function ff=imgaussflpf(I,sigma)
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j)= exp( -((i-M/2)^2+(j-N/2)^2) /2/(sigma^2) ); %高斯函数
end
end3.32 高斯滤波器应用
% gauss低通滤波器应用 gauss_exe.m
I1=imread('baby.bmp');
I=imnoise(I1,'salt & pepper');
%生成滤镜 (sigma=20)
ff=imgaussflpf(I,20);
%应用滤镜,频域滤波
out=imfreqfilt(I,ff);
%生成滤镜 (sigma=40)
ff1=imgaussflpf(I,40);
%应用滤镜,频域滤波
out1=imfreqfilt(I,ff1);
%生成滤镜 (sigma=60)
ff2=imgaussflpf(I,60);
%应用滤镜,频域滤波
out2=imfreqfilt(I,ff2);
%显示空间域图像
subplot(1,4,1);
imshow(I);
title('原图');
subplot(1,4,2);
imshow(out);
title('sigma=20');
subplot(1,4,3);
imshow(out1);
title('sigma=40');
subplot(1,4,4);
imshow(out2);
title('sigma=60');
%显示频域图像(fft--fftshift--abs--log)
If=fft2(I);
If=fftshift(If);
If=abs(If); %幅度谱
If=log(1+If); %压缩范围
outf=fft2(out);
outf=fftshift(outf);
outf=abs(outf); %幅度谱
outf=log(1+outf); %压缩范围
out1f=fft2(out1);
out1f=fftshift(out1f);
out1f=abs(out1f); %幅度谱
out1f=log(1+out1f); %压缩范围
out2f=fft2(out2);
out2f=fftshift(out2f);
out2f=abs(out2f); %幅度谱
out2f=log(1+out2f); %压缩范围
figure,
subplot(1,4,1);
imshow(If,[]);
title('原图');
subplot(1,4,2);
imshow(outf,[]);
title('sigma=20');
subplot(1,4,3);
imshow(out1f,[]);
title('sigma=40');
subplot(1,4,4);
imshow(out2f,[]);
title('sigma=60');(1)横向比较:高斯低通滤波器本身
1、由上图可知,sigma=40时,有较好的滤波效果(相较于sigma=20,60)
2、sigma值越小,gauss二维滤镜越瘦,截止频率越低;(频域与空域是相反,sigma越小,空域Gauss越胖,频域Gauss越瘦)。
(2)纵向比较:高斯和低通滤波相比
高斯相比于低通滤波,在有效抑制噪声的同时,图像的模糊程度更低,对边缘带来的混叠程度更小,从而使得Gauss比ideal有更为广泛的应用。
四、频域高通滤波器
图像锐化可以通过衰减频域中的低频信号来实现,这就建立了空间域图像锐化与频域高通滤波之间的关系。
4.1 高斯高通滤波器
4.11 构造高斯高通滤镜
%高斯高通滤波器滤镜 imgaussfhpf.m
%{
函数: function ff=imgaussfhpf(I,sigma)
函数说明:构造高斯高通滤镜
参数说明:I:输入图像
sigma:标准差
返回值:与原图像等大的高斯高通滤镜
%}
function ff=imgaussfhpf(I,sigma)
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j)= 1-exp( -((i-M/2)^2+(j-N/2)^2) /2/(sigma^2) ); % 1-(gauss)
end
end
% gauss高通滤波器应用 gaussHigh_exe.m
I=imread('coin.png');
%若是RGB,需转换为Gray
if(ndims(I)==3 && (size(I,3)==3) ) %RGB图像 size(I,3)表示I的第三维分量大小,ndims(I)代表I的维数
I=rgb2gray(I);
end
%生成滤镜 (sigma=20)
ff=imgaussfhpf(I,20);
%应用滤镜,频域滤波
out=imfreqfilt(I,ff);
%生成滤镜 (sigma=40)
ff1=imgaussfhpf(I,40);
%应用滤镜,频域滤波
out1=imfreqfilt(I,ff1);
%生成滤镜 (sigma=60)
ff2=imgaussfhpf(I,60);
%应用滤镜,频域滤波
out2=imfreqfilt(I,ff2);
%显示空间域图像
subplot(1,4,1);
imshow(I);
title('原图');
subplot(1,4,2);
imshow(out);
title('sigma=20');
subplot(1,4,3);
imshow(out1);
title('sigma=40');
subplot(1,4,4);
imshow(out2);
title('sigma=60');
%显示频域图像(fft--fftshift--abs--log)
If=fft2(I);
If=fftshift(If);
If=abs(If); %幅度谱
If=log(1+If); %压缩范围
outf=fft2(out);
outf=fftshift(outf);
outf=abs(outf); %幅度谱
outf=log(1+outf); %压缩范围
out1f=fft2(out1);
out1f=fftshift(out1f);
out1f=abs(out1f); %幅度谱
out1f=log(1+out1f); %压缩范围
out2f=fft2(out2);
out2f=fftshift(out2f);
out2f=abs(out2f); %幅度谱
out2f=log(1+out2f); %压缩范围
figure,
subplot(1,4,1);
imshow(If,[]);
title('原图');
subplot(1,4,2);
imshow(outf,[]);
title('sigma=20');
subplot(1,4,3);
imshow(out1f,[]);
title('sigma=40');
subplot(1,4,4);
imshow(out2f,[]);
title('sigma=60');
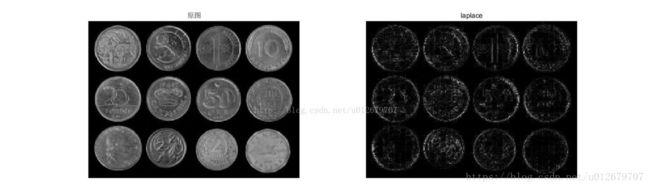
滤波结果:
结果分析:
1、高斯高通滤波器可以较好的提取边缘信息;
2、sigma越小,Gauss高通的截止频率越低,通过的低频成分越多,边缘提取越不精确,会包含更多的非边缘信息;(要求太低,多了浑水摸鱼者)
3、sigma越大,边缘提取越精确,但可能包含不完整的边缘信息。(要求太高,有了漏网之鱼)
4.2 拉普拉斯滤波器
4.21 构造laplace滤镜
应用laplace算子构造滤镜。
%laplace滤波器滤镜 imlapf.m
%{
函数: function ff=imlapf(I)
函数说明:构造laplace滤镜
参数说明:I:输入图像
返回值:与原图像等大的laplace滤镜
%}
function ff=imlapf(I)
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j)= -((i-M/2)^2+(j-N/2)^2) %
end
end
4.22 laplace滤波器应用
% laplace低通滤波器应用 laplace_exe.m
I=imread('coin.png');
%若是RGB,需转换为Gray
if(ndims(I)==3 && (size(I,3)==3) ) %RGB图像 size(I,3)表示I的第三维分量大小,ndims(I)代表I的维数
I=rgb2gray(I);
end
%生成滤镜
ff=imlapf(I);
%应用滤镜,频域滤波
out=imfreqfilt(I,ff);
%显示空间域图像
subplot(1,2,1);
imshow(I);
title('原图');
subplot(1,2,2);
imshow(out);
title('laplace');
%显示频域图像(fft--fftshift--abs--log)
If=fft2(I);
If=fftshift(If);
If=abs(If); %幅度谱
If=log(1+If); %压缩范围
outf=fft2(out);
outf=fftshift(outf);
outf=abs(outf); %幅度谱
outf=log(1+outf); %压缩范围
figure,
subplot(1,2,1);
imshow(If,[]);
title('原图');
subplot(1,2,2);
imshow(outf,[]);
title('laplace');
五、频域带阻滤波器
5.1 理想带阻滤波器
5.2高斯带阻滤波器
5.21 构造高斯带阻滤波器
%高斯带阻滤波器滤镜 imgaussfbrf.m
%{
函数: function ff=imgaussfbrf(I,freq,width)
函数说明:构造高斯带阻滤镜
参数说明:I:输入图像
freq:阻带中心频率
width:阻带宽度
返回值:与原图像等大的高斯带阻滤镜
%}
function ff=imgaussfbrf(I,freq,width)
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j)= 1-exp( -0.5*((((i-M/2)^2+(j-N/2)^2)-freq^2) /(sqrt(i.^2+j.^2)*width))^2); %高斯函数
end
end
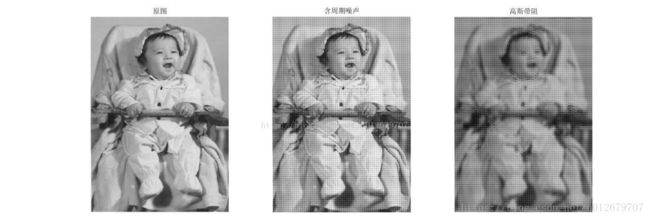
5.22 带阻滤波器应用--消除周期噪声
% gauss带阻滤波器应用 gaussBrf_exe.m
I1=imread('baby.bmp');
%产生周期噪声
[M,N]=size(I1);
I=I1;
for i=1:M
for j=1:N
I(i,j)= I(i,j)+20*sin(20*i) +20*sin(20*j) ; %添加周期噪声
end
end
%生成滤镜
ff=imgaussfbrf(I,50,5);
%应用滤镜,频域滤波
out=imfreqfilt(I,ff);
%显示空间域图像
subplot(1,3,1);
imshow(I1);
title('原图');
subplot(1,3,2);
imshow(I);
title('含周期噪声');
subplot(1,3,3);
imshow(out);
title('高斯带阻');
%显示频域图像(fft--fftshift--abs--log)
I1f=fft2(I1);
I1f=fftshift(I1f);
I1f=abs(I1f); %幅度谱
I1f=log(1+I1f); %压缩范围
If=fft2(I);
If=fftshift(If);
If=abs(If); %幅度谱
If=log(1+If); %压缩范围
outf=fft2(out);
outf=fftshift(outf);
outf=abs(outf); %幅度谱
outf=log(1+outf); %压缩范围
figure,
subplot(1,3,1);
imshow(I1f,[]);
title('原图');
subplot(1,3,2);
imshow(If,[]);
title('含周期噪声');
subplot(1,3,3);
imshow(outf,[]);
title('高斯带阻');
结果分析:
由最后一幅图可知,带阻滤波器在频域中为一圆环。圆环的位置与宽度由滤波器的中心频率和带宽决定。
------------------------------------------- END -------------------------------------