机器学习中梯度下降（Gradient Descent）的来龙去脉(第一部分)

这篇博客主要是想介绍一下自己对梯度下降的理解，在以往学习过程中我陷入了两个误区。

• 误区1：不求甚解，只是知道梯度下降是用来参数调优的一种方法。
• 误区2：死钻牛角尖，陷入梯度下降的数学过程中无法自拔。

---

前些日自己重新梳理了一下这部分内容，又学习了一下台湾李宏毅老师的视频课程，茅塞顿开，因此在这里做一下整理，和大家一起讨论。

---

既然想讲介绍的是梯度下降的来龙去脉，我将从以下角度展开讲解，首先简介梯度是什么，然后讲解为什么机器学习中会用到梯度下降，重点讲解机器学习中梯度下降的使用方法，最后再尽量补充一些梯度下降背后更深层次的数学机理。总而言之也就是是什么，为什么，怎么做。

梯度是什么

1 .一元函数的导数和微分

梯度是一个方向，沿这个方向函数变化最快。对于一元函数来说，函数 f(x) f ( x ) 只能随自变量 x x 变化，也就是只能沿 x x 轴方向变化，而在某一点 x0 x 0 变化的快慢则可以用这一点的斜率即导数 f′(x0) f ′ ( x 0 ) 来表示。更近一步用图1来说明一元函数的微分，一元微分 dy d y 代表的是切线的增量，常常用它来近似函数的变化量，也就是微积分的精髓“以直代曲”。

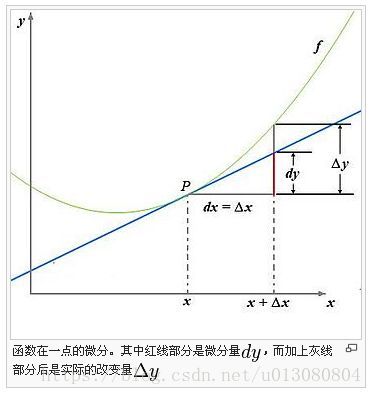
图1 一元函数的导数和微分

现在我们已经回顾了一元函数的导数和微分，对于多元函数，后面都用二元函数 z=f(x,y) z = f ( x , y ) 为例来说明多元函数的梯度是什么东东。（因为三元或超多元函数的图像实在是太难画了）。

2.多元函数的偏导，方向导数和梯度

• 偏导
  对于多元函数 f(x,y) f ( x , y ) 来说，函数的图像通常是一个曲面。而你在曲面上由一个点 (x0,y0) ( x 0 , y 0 ) 走到另一个点 (x1,y1) ( x 1 , y 1 ) 也只能是走一条路径（曲线）出来，而从一个点走到另一个点会有无数种不同的走法。
  
  
  
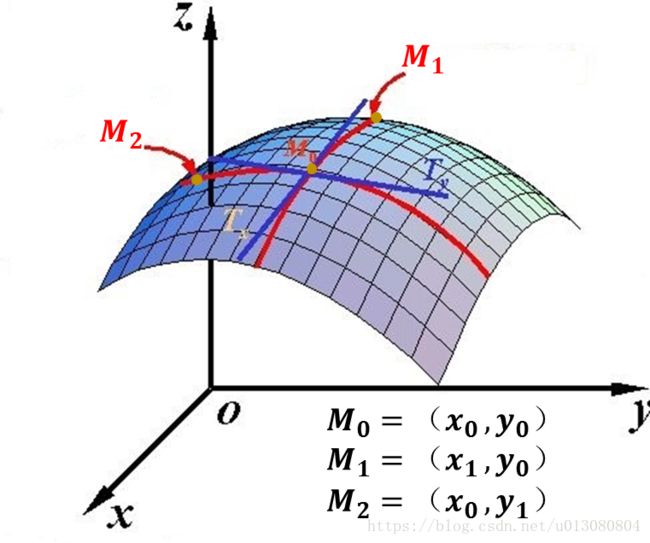
  首先我们考虑简单的，即我们只沿坐标轴方向走，如上图所示。如果我们只沿 x x 轴方向走，即从 M0 M 0 点走到 M1 M 1 点，很显然路径就是这两点之间的红色部分，这个路径处于 y=y0 y = y 0 和我们的曲面的交线上。如果我们想知道我们沿着这个路径走多快就能到达，那么就类似于一元函数，只需要在这一点对这条路做切线 TX T X ，切线对 x x 轴的斜率即为这一点的偏导数 f′x(x0,y0) f x ′ ( x 0 , y 0 ) .而 f′y(x0,y0) f y ′ ( x 0 , y 0 ) 与之类似。
  现在我们总结一下偏导数即函数在某一点方向沿坐标轴方向的变化率。事实上过 M0 M 0 点不有无数条曲线，无数条路径，每一条路径都可以表示我们沿某一方向前行。而对这一条路径在 M0 M 0 点做切线即可得到函数沿这一方向的变化率，所以，方向导数的概念就出来了，函数沿某一方向的变化率即方向导数。
• 方向导数
  那么方向导数如何求呢？ x x 方向和 y y 方向的斜率可以由偏导求得，那么我们可以用这两个偏导来表示任何方向的斜率即方向导数（类似于一个平面内的所有向量可以用两个基向量来表示，不知道为什么好像我们的高数很少说这一点，只是告诉我们怎么计算）。现在我们有这个需求，想求出 u u 方向的斜率怎么办。同样假设 z=f(x,y) z = f ( x , y ) 为一个曲面， p(x0，y0) p ( x 0 ， y 0 ) 为定义域上任意一点，任意单位向量 u=cosθi+sinθj u = c o s θ i + s i n θ j 其中 θ θ 为向量 u u 与 x x 轴的夹角，当 θ θ 不断变化时向量 u u 可以取任意方向，如下图所示。
  
  
  
  
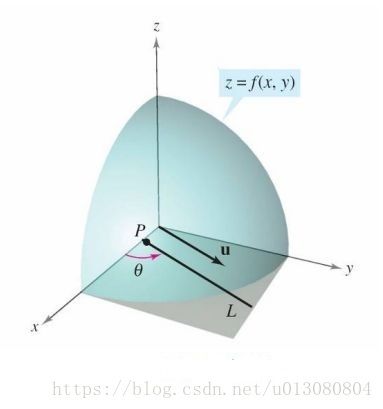
  • 梯度
    同时可以证明 Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ D u f ( x , y ) = f x ( x , y ) c o s θ + f y ( x , y ) s i n θ 。此时，设 A=(fx(x,y),fy(x,y)) A = ( f x ( x , y ) , f y ( x , y ) ) ,同样可以证明沿这个方向 Duf(x,y) D u f ( x , y ) 值最大。那么这个方向即为梯度！证明过程我会在下一篇博客详细证明，即为什么梯度方向为变化最快的方向，也会顺便证明 Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ D u f ( x , y ) = f x ( x , y ) c o s θ + f y ( x , y ) s i n θ 这个等式。

---

好了啰嗦了这么多，相信大家对于什么是梯度有了一定了解，下面我会讲解为什么机器学习中会用到梯度下降，这里主要是参考李宏毅老师的视频课程来讲解，同样链接会放在文末。

为什么采用梯度下降

首先我们机器学习，简单来说就是要find一个function，而这个function可以根据我们的input返回一个值，当然这个function里面包含许多参数，这些参数取哪些值是需要我们学习的，而梯度下降正是我们学习参数的一个好方法。
这里冒昧的借用李老师的例子。即假如我们手里有 10 10 只神奇宝贝的资料，我们知道其中每只神奇宝贝进化前的 cp c p 值和进化后的 cp c p 值，想用这些数据来预测其他任意一只神奇宝贝进化后的 cp c p 值。
那么我们假设神奇宝贝进化前和进化后的 cp c p 值可以用以下函数 f(x) f ( x ) 表示：

y=b+w∗x y = b + w ∗ x

其中 x x 是进化前的 cp c p 值， y y 是进化后的。其中， w w 和 b b 可以取任何值，那么我们可以用这个函数对我们所有的这十只神奇宝贝的拟合程度来反映这组参数的好坏。即如以下公式：

L(f)=L(W,B)=∑i=110(y^n−(b+w∗xn))2 L ( f ) = L ( W , B ) = ∑ i = 1 10 ( y ^ n − ( b + w ∗ x n ) ) 2

L L 越小，说明函数拟合效果越好，这组参数就越优。因此，我们的目标就是找到一组参数使 L L 最小。 即如以下公式：

w∗,b∗=argminw,b∑i=110(y^n−(b+w∗xn))2 w ∗ , b ∗ = arg ⁡ min w , b ⁡ ∑ i = 1 10 ( y ^ n − ( b + w ∗ x n ) ) 2

通常的做法是我们随机选取一个初始的参数 (w0,b0) ( w 0 , b 0 ) ,然后我们想不断寻找到函数 L(w,b) L ( w , b ) 的最低点，最低点的位置 （w∗,b∗） （ w ∗ , b ∗ ） 即为我们想要的最优参数。
那么我们怎么才能找到这个最低点呢，如下图所示，这就需要用到梯度啦，既然梯度是函数变化最快的方向，那我们让函数沿梯度方向一直走，设置合适的步长，岂不是就可以到达这个最低点啦。

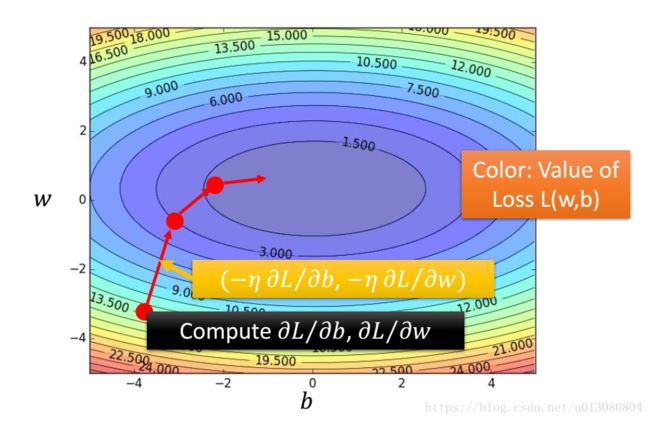
即我们初始选取参数为 （w0,b0） （ w 0 , b 0 ） ,然后我们设置合适的步长 η η ,下一时刻 （w1,b1） （ w 1 , b 1 ） 为：

（w1,b1）=(w0,b0)−η∇L （ w 1 , b 1 ） = ( w 0 , b 0 ) − η ∇ L

而 ∇L ∇ L 即为函数在 （w0,b0） （ w 0 , b 0 ） 的梯度，如下所示：

∇L(w0,b0)=[δLδw|(w0,b0),δLδb|(w0,b0)]T ∇ L ( w 0 , b 0 ) = [ δ L δ w | ( w 0 , b 0 ) , δ L δ b | ( w 0 , b 0 ) ] T

然后按照上述公式不断迭代，最后我们就可以取得一个较优的 (w,b) ( w , b ) 值，当然在实际操作过程中会有很多技巧，我同样会在下一篇博客中讲解。

---

到这，我自认为算是讲清楚了梯度下降的来龙，当然也参考了知乎上的好多回答，希望读者可以和我讨论交流。这里我强烈推荐观看李老师的视频课程，李老师台湾口音，让我有一种看偶像剧的感觉，很奇妙。

---

参考文献

[1]知乎关于梯度下降讲解的连接：https://www.zhihu.com/question/36301367#answer-22165770
[2]李宏毅的机器学习课程：http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML16.html

---

初夏很让人焦躁不安，希望我能够尽快写出下一篇，尽量在盛夏，不要拖到秋季。