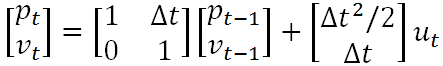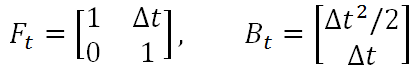参考链接:
这篇复制粘贴了网上很多讲卡尔曼的文章:
https://blog.csdn.net/App_12062011/article/details/51758989
这篇是卡尔曼滤波的opencv实例:
https://www.cnblogs.com/21207-iHome/p/5238242.html
tracking的传统方法的综述:几年前的:
https://zhuanlan.zhihu.com/p/32453407
OpenCV写代码:
https://blog.csdn.net/gdfsg/article/details/50904811
MATLAB相关的卡尔曼滤波:
https://www.mathworks.com/help/vision/examples/using-kalman-filter-for-object-tracking.html#d117e5368
https://blog.csdn.net/Kerrwy/article/details/81120259
零、引入
参考网站:https://www.jianshu.com/p/d51a3a7736ca
假设我们要研究的对象是一个房间的温度。根据你的经验判断,这个房间的温度是恒定的,也就是下一分钟的温度等于现在这一分钟的温度(假设我们用一分钟来做时间单位)。假设你对你的经验不是100%的相信,可能会有上下偏差几度。我们把这些偏差看成是高斯白噪声(White Gaussian Noise),也就是这些偏差跟前后时间是没有关系的而且符合高斯分布(Gaussian Distribution)。另外,我们在房间里放一个温度计,但是这个温度计也不准确的,测量值会比实际值偏差。我们也把这些偏差看成是高斯白噪声。
好了,现在对于某一分钟我们有两个有关于该房间的温度值:你根据经验的预测值(系统的预测值)和温度计的值(测量值)。下面我们要用这两个值结合他们各自的噪声来估算出房间的实际温度值。
假如我们要估算k时刻的实际温度值。首先你要根据k-1时刻的温度值,来预测k时刻的温度。因为你相信温度是恒定的,所以你会得到k时刻的温度预测值是跟k-1时刻一样的,假设是23度,同时该值的高斯噪声的偏差是5度(5是这样得到的:如果k-1时刻估算出的最优温度值的偏差是3,你对自己预测的不确定度是4度,他们平方相加再开方,就是5)。然后,你从温度计那里得到了k时刻的温度值,假设是25度,同时该值的偏差是4度。
由于我们用于估算k时刻的实际温度有两个温度值,分别是23度和25度。究竟实际温度是多少呢?相信自己还是相信温度计呢?究竟相信谁多一点,我们可以用他们的covariance来判断。因为Kg=52/(52+4^2),所以Kg=0.61,我们可以估算出k时刻的实际温度值是:23+0.61(25-23)=24.22度。可以看出,因为温度计的covariance比较小(比较相信温度计),所以估算出的最优温度值偏向温度计的值。
现在我们已经得到k时刻的最优温度值了,下一步就是要进入k+1时刻,进行新的最优估算。到现在为止,好像还没看到什么自回归的东西出现。对了,在进入k+1时刻之前,我们还要算出k时刻那个最优值(24.22度)的偏差。算法如下:((1-Kg)
52)0.5=3.12。这里的5就是上面的k时刻你预测的那个23度温度值的偏差,得出的3.12就是进入k+1时刻以后k时刻估算出的最优温度值的偏差(对应于上面的3)。
就是这样,卡尔曼滤波器就不断的把covariance递归,从而估算出最优的温度值。他运行的很快,而且它只保留了上一时刻的covariance。上面的Kg,就是卡尔曼增益(Kalman Gain)。他可以随不同的时刻而改变他自己的值,是不是很神奇!
一、公式推导和原理理解
第一个公式:
假如现在有一辆在路上做直线运动的小车(如下所示),该小车在 t 时刻的状态可以用一个向量来表示,其中pt表示他当前的位置,vt表示该车当前的速度。当然,司机还可以踩油门或者刹车来给车一个加速度ut,ut相当于是一个对车的控制量。显然,如果司机既没有踩油门也没有踩刹车,那么ut就等于0。此时车就会做匀速直线运动。
如果我们已知上一时刻 t-1时小车的状态,现在来考虑当前时刻t小车的状态。显然有
易知,上述两个公式中,输出变量都是输入变量的线性组合,这也就是称卡尔曼滤波器为线性滤波器的原因所在。既然上述公式表征了一种线性关系,那么我们就可以用一个矩阵来表示它,则有
如果另其中的
则得到卡尔曼滤波方程组中的第一条公式——状态预测公式,而Ft就是状态转移矩阵,它表示我们如何从上一状态来推测当前状态。而B则是控制矩阵,它表示控制量u如何作用于当前状态。
上式中x顶上的hat表示为估计值(而非真实值)。等式左端部分的右上标“-”表示该状态是根据上一状态推测而来的,稍后我们还将对其进行修正以得到最优估计,彼时才可以将“-”去掉。
第二个公式:
既然我们是在对真实值进行估计,那么就理应考虑到噪声的影响。实践中,我们通常都是假设噪声服从一个0均值的高斯分布,即Noise~Guassian(0,σ)。例如对于一个一维的数据进行估计时,若要引入噪声的影响,其实只要考虑其中的方差σ即可。当我们将维度提高之后,为了综合考虑各个维度偏离其均值的程度,就需要引入协方差矩阵。
回到我们的例子,系统中每一个时刻的不确定性都是通过协方差矩阵 Σ 来给出的。而且这种不确定性在每个时刻间还会进行传递。也就是说不仅当前物体的状态(例如位置或者速度)是会(在每个时刻间)进行传递的,而且物体状态的不确定性也是会(在每个时刻间)进行传递的。这种不确定性的传递就可以用状态转移矩阵来表示,即(注意,这里用到了前面给出的关于协方差矩阵的性质)
但是我们还应该考虑到,预测模型本身也并不绝对准确的,所以我们要引入一个协方差矩阵 Q 来表示预测模型本身的噪声(也即是噪声在传递过程中的不确定性),则有
这就是卡尔曼滤波方程组中的第二条公式,它表示不确定性在各个时刻间的传递关系。
第三个公式:
继续我们的小汽车例子。你应该注意到,前面我们所讨论的内容都是围绕小汽车的真实状态展开的。而真实状态我们其实是无法得知的,我们只能通过观测值来对真实值进行估计。所以现在我们在路上布设了一个装置来测定小汽车的位置,观测到的值记为Y(t)。而且从小汽车的真实状态X(t)到其观测状态还有一个变换关系,这个变换关系我们记为h(•),而且这个h(•)还是一个线性函数。此时便有:
Y(t) = h[X(t)] + V(t)
其中V(t)表示观测的误差。既然h(•)还是一个线性函数,所以我们同样可以把上式改写成矩阵的形式,则有
Yt=Hxt + v
就本例而言,观测矩阵 H = [1 0],这其实告诉我们x和Z(就是h[X(t)] + V(t))的维度不一定非得相同。在我们的例子中,x是一个二维的列向量,而Z(本例中即Yt)只是一个标量。此时当把x与上面给出的H相乘就会得出一个标量,此时得到的Y就是x中的首个元素,也就是小车的位置。同样,我们还需要用一个协方差矩阵R来取代上述式子中的v来表示观测中的不确定性。当然,由于Z是一个一维的值,所以此时协方差矩阵R也只有一维,也就是只有一个值,即观测噪声之高斯分布的参数σ。如果我们有很多装置来测量小汽车的不同状态,那么Z(本例中即Yt)就会是一个包含所有观测值的向量。
接下来要做的事情就是对前面得出的状态估计进行修正,具体而言就是利用下面这个式子
yt为实际观察值。
第四个公式:
前面我们提到,
是根据上一状态推测而来的,那么它与“最优”估计值之间的差距现在就是等式右端加号右侧的部分。
表示实际观察值与预估的观测值之间的残差。这个残差再乘以一个系数K就可以用来对估计值进行修正。K称为卡尔曼系数,它也是一个矩阵,它是对残差的加权矩阵,有的资料上称其为滤波增益阵。
定性解读如下:
滤波增益阵首先权衡预测状态协方差矩阵Σ 和观测值矩阵R的大小,并以此来觉得我们是更倾向于相信预测模型还是详细观测模型。如果相信预测模型多一点,那么这个残差的权重就会小一点。反之亦然,如果相信观察模型多一点,这个残差的权重就会大一点。
不仅如此,滤波增益阵还负责把残差的表现形式从观测域转换到了状态域。例如本题中观测值Z(本例中即Yt)仅仅是一个一维的向量,状态 x (包含小车的位置和速度)是一个二维的向量。所以在实际应用中,观测值与状态值所采用的描述特征或者单位都有可能不同,显然直接用观测值的残差去更新状态值是不合理的。而利用卡尔曼系数,我们就可以完成这种转换。例如,在小车运动这个例子中,我们只观察到了汽车的位置,但K里面已经包含了协方差矩阵sigma的信息(sigma里面就给出了速度和位置的相关性),所以它利用速度和位置这两个维度的相关性,从位置的残差中推算出了速度的残差。从而让我们可以对状态值 x 的两个维度同时进行修正。
详细推导参考文献:【1】秦永元,张洪钺,汪叔华,卡尔曼滤波与组合导航原理,西北工业大学出版社 的第35-37页
第五个公式:
最后,还需对最优估计值的噪声分布进行更新。所使用的公式为
总结:
至此,我们便获得了实现卡尔曼滤波所需的全部五个公式:
我们将这五个公式分成预测组和更新组。预测组总是根据前一个状态来估计当前状态。更新组则根据观测信息来对预测信息进行修正,以期达到最优估计之目的。
整个卡尔曼滤波的算法基本如下:
参考网页:https://zhuanlan.zhihu.com/p/21692854
二、MATLAB简单实例
当然,你可能困惑于卡尔曼滤波是否真的有效。下面利用参考文件【2】卡尔曼滤波的原理以及在MATLAB中的实现,http://blog.csdn.net/revolver/article/details/37830675 中给出的例子来演示卡尔曼滤波的威力。这个例子模拟质点进行匀速直线运动(速度为1),然后引入一个非常大的噪声,再用卡尔曼滤波来对质点的运动状态进行轨迹。注意是匀速直线运动,所以其中不含有控制变量(即加速度)。
%观测值(含噪声)
Z = (1:100);%真实值
noise = randn(1,100);
Z = Z +noise;
%状态值的初始化
X = [0;0];%二维,代表起始时,该点的位置和速度
Sigma = [1 0 ; 0 1];%状态转移协方差矩阵
F = [1 1;0 1]; %delta t = 1
Q = [0.0001 0;0 0.0001];%状态转移协方差矩阵的噪声矩阵
H = [1 0];
R = 1;
figure;
hold on;
for i = 1:100
X_ = F*X;
Sigma_ = F*Sigma*F'+Q;
K = Sigma_*H'/(H*Sigma_*H'+R);
%/的速度比inv快
X = X_ +K*(Z(i) - H* X_);
Sigma = (eye(2) - K*H)*Sigma_;
%eye是对角线元素为1的矩阵
plot(X(1),X(2),'.','MarkerSize',10)
%画点,横轴表示位置,纵轴表示速度。
end
plot([0,100],[1,1],'r-')
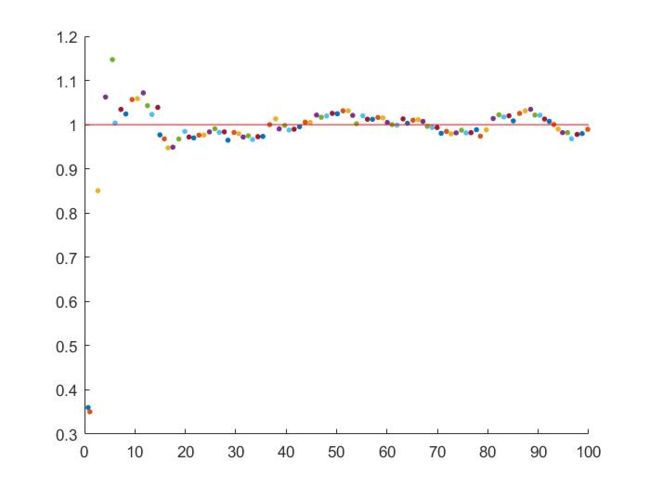
结果如下:
下图给出了上述代码的执行结果。可见经过最开始的几次迭代后,质点运动的状态估计就回到了正确轨迹上,而且估计的结果基本围绕在真实值附近,效果还是很理想的。
三、用MATLAB进行小球位置预测
参考网站:https://www.mathworks.com/help/vision/examples/using-kalman-filter-for-object-tracking.html
中文翻译版本:https://blog.csdn.net/Kerrwy/article/details/81120259
四、用MATLAB进行多目标位置跟踪
https://www.mathworks.com/help/vision/examples/motion-based-multiple-object-tracking.html
五、用卡尔曼滤波进行自己的数据的跟踪
1.把待测数据通过Unet test,得到经过Unet segment之后的分割图
(1)用label的图片或者segmented的图片作为input,我暂时用tif格式的。
(2)直接下载singleball.mp4跑一下源代码
遇到问题1:无法调用matlab自定义函数
参考网站:https://www.ilovematlab.cn/thread-134014-1-1.html
解决办法:新建的时候新建错了吧 不要新建 script文件 可以选择新建function的 就能使用定义function了。成功解决。
遇到问题2:报错未定义变量 "utilities" 或类"utilities.videoReader"。
解决办法:在对应子函数的开头加上:param = getDefaultParameters(); utilities = createUtilities(param);
遇到问题3:未定义函数或变量 'frame', 'detectedLocation',。
解决办法:global一下frame变量
遇到问题4:tracking部分第12行报错:matlab运算符异常。
解决办法:global utilities.foregroundMask 这样不行
各种bug。。。。。。
六、卡尔曼滤波器调参需要注意的事项
应根据探测器的精度选择MeasurementNoise的值。 测量噪声设置为较大的值会获得不太精确的检测器。 以下示例说明了错误配置的分段阈值的噪声检测。 增加测量噪声会导致卡尔曼滤波器更多地依赖于其内部状态而不是输入的测量值,从而补偿检测噪声。
通常,物体不会以恒定的加速度或恒定的速度移动。 您可以使用MotionNoise指定与理想运动模型的偏差量。 当您增加运动噪声时,卡尔曼滤波器更多地依赖于输入测量而不是内部状态。 尝试使用MotionNoise参数进行试验,以了解有关其效果的更多信息。
七、试试这个toolbox
https://github.com/rlabbe/filterpy
安装:pip install filterpy
介绍:Python Kalman filtering and optimal estimation library. Implements Kalman filter, particle filter, Extended Kalman filter, Unscented Kalman filter, g-h (alpha-beta), least squares, H Infinity, smoothers, and more. Has companion book 'Kalman and Bayesian Filters in Python'.
中文翻译在这里:https://github.com/loveuav/Kalman-and-Bayesian-Filters-in-Python
先读设计这一章:
https://github.com/loveuav/Kalman-and-Bayesian-Filters-in-Python/blob/chinese/08-%E8%AE%BE%E8%AE%A1%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2%E5%99%A8.ipynb