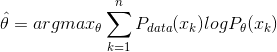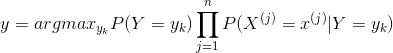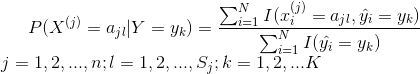生成模型与判别模型的区别与联系
1、概述
监督学习的任务就是学习一个模型,应用这一模型,对给定的输入预测相应的输出。这个模型的一般形式为决策函数:
![]()
或者条件概率分布:
![]()
监督学习方法又可以分为生成方法(generative approach)和判别方法(discriminative approach)。所学到的模型分别称为生成模型(generative model)和判别模型(discriminative model)。
2、判别模型
2.1 判别方法的定义
判别方法由数据直接学习决策函数![]() 或者条件概率分布
或者条件概率分布![]() 作为预测的模型,即判别模型。判别方法关心的是对给定的输入
作为预测的模型,即判别模型。判别方法关心的是对给定的输入![]() ,应该预测什么样的输出
,应该预测什么样的输出![]() 。典型的判别模型包括:k近邻法、感知机、决策树等。
。典型的判别模型包括:k近邻法、感知机、决策树等。
2.2 判别模型的思想
判别模型直接对条件概率![]() 建模,基本思想是在有限样本条件下,建立判别函数,直接研究预测模型。下面我们利用贝叶斯决策论里面的知识,利用判别方法对测试数据进行建模求解。
建模,基本思想是在有限样本条件下,建立判别函数,直接研究预测模型。下面我们利用贝叶斯决策论里面的知识,利用判别方法对测试数据进行建模求解。
这里定义训练数据为![]() ,
,![]() 是n个训练样本的标签,
是n个训练样本的标签,![]() 是n个训练样本的特征。定义单个测试数据为
是n个训练样本的特征。定义单个测试数据为![]() ,
,![]() 为测试数据的类别,
为测试数据的类别,![]() 是测试样本的特征。
是测试样本的特征。
训练完毕后,输入测试数据,判别模型直接给出的是![]() ,即输出(类别)关于输入(特征)的条件分布,实际上,这个分布的条件还有训练数据---------因为实际上我们是“看过”训练数据之后,学习到了对数据分布的后验认识,然后根据这个认识和测试样本的特征来做出测试样本属于哪个类别的决策的,所以有
,即输出(类别)关于输入(特征)的条件分布,实际上,这个分布的条件还有训练数据---------因为实际上我们是“看过”训练数据之后,学习到了对数据分布的后验认识,然后根据这个认识和测试样本的特征来做出测试样本属于哪个类别的决策的,所以有![]() 。
。
我们认为这个条件分布![]() 由参数
由参数![]() 决定的,即
决定的,即![]() ……(2.1)
……(2.1)
那么如何由![]() 得到
得到![]() 呢?如果我们可以求出参数
呢?如果我们可以求出参数![]() 关于训练数据的的后验分布
关于训练数据的的后验分布![]() (这其实就是学习过程),那么就可以由
(这其实就是学习过程),那么就可以由
![]() ……(2.2)
……(2.2)
来得到想要的答案(关于②如何得到,请参考其他地方的讨论PRML第一章公式1.68如何推导? - 机器学习 - 知乎,第31页公式1.68怎么推导的啊..)。
所以现在问题转化成了求条件分布的参数![]() 关于训练数据
关于训练数据![]() 的后验分布
的后验分布![]() 。那么我们来看看怎么求这个后验分布。条件分布关于训练数据的似然函数
。那么我们来看看怎么求这个后验分布。条件分布关于训练数据的似然函数
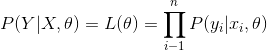 ……(2.3)
……(2.3)
有没有发现![]() 和
和![]() 有一点像?像是
有一点像?像是![]() 和Y互换了位置,互为条件概率,可以考虑使用贝叶斯公式来进行转化,即
和Y互换了位置,互为条件概率,可以考虑使用贝叶斯公式来进行转化,即
![]() ……(2.4)
……(2.4)
所以现在问题又进行了转化,变成了求条件分布关于训练数据的似然函数、参数![]() 的先验分布和Y关于X的条件分布三个小问题。我们已经知道似然函数怎么求,先验分布也不需要求(先验知识,就是我们在解决问题之前已经知道的知识,在这里就是我们认为参数是未观察到的随机变量,其本身也可有分布【贝叶斯学派】),而
的先验分布和Y关于X的条件分布三个小问题。我们已经知道似然函数怎么求,先验分布也不需要求(先验知识,就是我们在解决问题之前已经知道的知识,在这里就是我们认为参数是未观察到的随机变量,其本身也可有分布【贝叶斯学派】),而
![]() ……(2.5)
……(2.5)
至此问题已经解决,综合上述(1)-(5)各式,我们终于可以求出输出关于输入的条件分布啦!
(6)中的两个积分的计算是很麻烦的,在实际解决问题的过程中要想办法省略掉。
对于(2)中积分公式可以使用variational inference的方法干掉,variational inference用一句话来说就是:如果训练样本足够多的话,可以使用![]() 的最大后验分布
的最大后验分布![]() 来对
来对![]() 进行点估计(point estimate)。即有:
进行点估计(point estimate)。即有:
![]() ……(2.7)
……(2.7)
所以我们干掉了第一个积分问题,把问题简化成了求![]() 的最大后验概率
的最大后验概率![]() 。
。
观察(2.4)式可以发现分母![]() 对于我们想要估计的问题而言,可以看作一个标量,如果我们省略掉(4)中的分母
对于我们想要估计的问题而言,可以看作一个标量,如果我们省略掉(4)中的分母![]() 对结果是没有影响的(只需要对分子进行normalize就可以得到后验概率
对结果是没有影响的(只需要对分子进行normalize就可以得到后验概率![]() ),那么我们又干掉了第二个积分公式,将问题简化成了求
),那么我们又干掉了第二个积分公式,将问题简化成了求![]() 的最大值。如果先验分布在似然函数较大的区间是固定不变或变化较小的,那么问题又可以转化成求最大似然函数!
的最大值。如果先验分布在似然函数较大的区间是固定不变或变化较小的,那么问题又可以转化成求最大似然函数!
实际上,在噪声高斯分布的假设下,最小误差平方和优化问题(即求使误差平方和最小的参数)等价于求最大似然函数(即使似然函数最大的参数)。
2.3 极大似然估计
似然(likelihood,可能性的意思),描述的是事件发生可能性的大小。
极大似然估计是频率主义学派的观点,主要就是根据采样来估计概率分布参数。
假设我们要根据样本所属的类别来对一组样本进行分类。这样我们就有c个样本集![]() 。
。![]() 表示训练集
表示训练集![]() 中第
中第![]() 类样本组成的集合,任意一个
类样本组成的集合,任意一个![]() 中的样本都是独立的根据类条件概率密度函数
中的样本都是独立的根据类条件概率密度函数![]() 来抽取的。因此我们可以成每一个样本集中的样本都是独立同分布的随机变量。我们还假设每一个类条件概率密度
来抽取的。因此我们可以成每一个样本集中的样本都是独立同分布的随机变量。我们还假设每一个类条件概率密度![]() 的形式是已知的,其未知的就是具体的参数向量
的形式是已知的,其未知的就是具体的参数向量![]() 。
。
数据集![]() 有n个样本
有n个样本![]() ,因为样本是独立同分布的,则参数
,因为样本是独立同分布的,则参数![]() 关于数据集
关于数据集![]() 的似然函数是:
的似然函数是:
对![]() 进行极大似然估计,就是去寻找能最大化似然
进行极大似然估计,就是去寻找能最大化似然![]() 的参数值
的参数值![]() 。直观上看,极大似然估计是试图寻找
。直观上看,极大似然估计是试图寻找![]() 所有可能取值中,找到一个能使数据出现的“可能性”的最大的值。
所有可能取值中,找到一个能使数据出现的“可能性”的最大的值。
然而使用连乘的操作易造成下溢,通常使用对数似然:
此时参数![]() 的极大似然估计
的极大似然估计![]() 为:
为:![]() ……(2.10)。
……(2.10)。
例如,在连续特征情形下,假设概率密度函数![]() ,则参数
,则参数![]() 和
和![]() 的极大似然估计为:
的极大似然估计为:
通过上式,我们可以发现,通过极大似然估计得到的正态分布均值就是样本均值,方差就是样本协方差,这显然也是一个符合直觉的结果。在离散特征情形下,也可以通过类似的方法估计类条件概率密度。
2.4 对数似然到分类问题
对数似然函数的表达式如(2.9)式所列,我们在右端除以n,代表我们从样本中采样的概率是均等的。表达式可以写为:
![]() ……(2.14)
……(2.14)
这里面![]() 代表每一个样本
代表每一个样本![]() 从真实样本数据中采样的概率,也就是假设真实数据的分布是均匀分布,而
从真实样本数据中采样的概率,也就是假设真实数据的分布是均匀分布,而![]() 相当于我们训练后的模型的预测标记分布对
相当于我们训练后的模型的预测标记分布对![]() 的采样概率,这样就可以表现为将
的采样概率,这样就可以表现为将![]() 看作交叉熵。
看作交叉熵。
当然,理论上,根据已有的数据,我们可以得到每个x的统计频率![]() ,那么(2.13)式的等价形式可以变为:
,那么(2.13)式的等价形式可以变为:
但是实际上,我们几乎都不可能得到![]() (尤其是连续分布),我们能直接算的是关于它的期望,也就是(2.14)式,因为求期望只需要把每个样本的值算出来,然后求和除以n就行了。所以(2.16)式只有理论价值,能够方便后面的推导。
(尤其是连续分布),我们能直接算的是关于它的期望,也就是(2.14)式,因为求期望只需要把每个样本的值算出来,然后求和除以n就行了。所以(2.16)式只有理论价值,能够方便后面的推导。
现在我们来看一下监督学习的分类问题是如何与最大似然联系在一起的。
假设我们有输入![]() ,标签
,标签![]() ,那么
,那么![]() 就构成了一个事件,X是训练数据集D中所有
就构成了一个事件,X是训练数据集D中所有![]() 的集合,Y是训练数据集D中所有
的集合,Y是训练数据集D中所有![]() 的集合于是我们根据(2.14)式就有:
的集合于是我们根据(2.14)式就有:
![]() ……(2.17)
……(2.17)
这样的一个对![]() 整体求数学期望的式子对我们而言,是不够实用的。以分类问题为例,我们通常建模的是
整体求数学期望的式子对我们而言,是不够实用的。以分类问题为例,我们通常建模的是![]() ,而不是
,而不是![]() ,也就是我们要根据输入确定输出的分布,而不是他们的联合分布,所有我们还是要从(2.16)式出发,先得到:
,也就是我们要根据输入确定输出的分布,而不是他们的联合分布,所有我们还是要从(2.16)式出发,先得到:
因为我们只对![]() 建模,因此
建模,因此![]() 就可以理解为
就可以理解为![]() 就是一个未知的常数了,优化模板有个常数项,可以省去,因此(18)式就等价于:
就是一个未知的常数了,优化模板有个常数项,可以省去,因此(18)式就等价于:
……(2.19)
其实![]() 就是已知训练数据的经验分布
就是已知训练数据的经验分布![]() ,条件概率分布
,条件概率分布![]() 的对数似然函数的表示。
的对数似然函数的表示。
然后,根据乘法公式,(2.19)式就等价于
与偶遇我们处理的是监督学习中的分类问题,一般而言在训练数据中对于确定的输入![]() 就只有一个类标
就只有一个类标![]() 与之对应,即
与之对应,即![]() ,其余都为0,
,其余都为0,![]() 就是
就是![]() 对应的真实的目标类别,所以:
对应的真实的目标类别,所以:
将(2.21)式写成期望的形式,就变成最常见的分类问题的极大似然函数:
![]() ……(2.22)
……(2.22)
当然,在分类问题中,使用极大似然函数也只是为了求出我们所建立的模型的参数,也就是说这个极大似然函数可以作为我们的优化目标,假如该极大似然函数是一个可以转换成一个凸优化问题,那我们就可以利用经典的数值优化算法如梯度下降法、牛顿法等来求解参数。
关于在这里写上极大似然到分类问题,只是为了承接上文。其实对于分类问题,无论是判别模型还是生成模型在贝叶斯的框架下,都可以这样理解。
2.4 判别模型总结
1、判别模型的求解形式:直接对决策函数或条件概率分布建模。
2、判别模型的求解思路:求解条件分布关于训练数据的似然函数(3)式,转化为模型参数后验概率最大(4)式,转化为(似然函数参数先验)最大,转化为最大似然(10)式。举例理解:我们训练神经网络的时候,就是在找一个能够最大限度使特征和类别标签能够对应上的参数。
3、判别模型的学习过程:
①明确要求解的问题。②建模。③设计目标函数,例如分类问题中,我们经常使用极大似然函数作为我们的目标函数。④利用优化方法求解目标函数的参数。
3、生成模型
3.1 生成方法的定义
生成方法由数据学习联合概率分布P(X,Y), 然后求出条件概率分布P(Y|X)作为预测的模型, 即生成模型:
![]() ……(3.1)
……(3.1)
这样的方法之所以称为生成方法, 是因为模型表示了给定输入X产生输出Y的生成关系。典型的生成模型有: 朴素贝叶斯法、深度学习里面的GAN、VAE等。
3.2 生成模型的思想
对于生成算法必然考虑(3.1)式。基于贝叶斯定理,(3.1)式可以写为:
其中,![]() 是类先验概率分布;
是类先验概率分布;![]() 是样本X相对于类标签Y的类条件概率,或称为“似然”;
是样本X相对于类标签Y的类条件概率,或称为“似然”;![]() 是用于归一化的“证据”因子。对于给定样本X,证据因子
是用于归一化的“证据”因子。对于给定样本X,证据因子![]() 与类标签无关,因此估计
与类标签无关,因此估计![]() 的问题就转化为如何基于训练数据D来估计先验
的问题就转化为如何基于训练数据D来估计先验![]() 和似然
和似然![]() 。
。
先验概率![]() 表达了样本空间中各类样本所占的比例,根据大数定律,当训练集包含充足的独立同分布的样本时,
表达了样本空间中各类样本所占的比例,根据大数定律,当训练集包含充足的独立同分布的样本时,![]() 可通过各类样本出现的频率来进行估计。
可通过各类样本出现的频率来进行估计。
对于类条件概率![]() 来说,由于它涉及关于X所有属性的联合概率,直接根据样本出现的频率来估计将会造成严重的困难。但朴素贝叶斯算法不这样看,它做出了一个极强的假设:特征条件独立。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。 这一假设使朴素贝叶斯法变得简单, 但有时会牺牲一定的分类准确率。
来说,由于它涉及关于X所有属性的联合概率,直接根据样本出现的频率来估计将会造成严重的困难。但朴素贝叶斯算法不这样看,它做出了一个极强的假设:特征条件独立。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。 这一假设使朴素贝叶斯法变得简单, 但有时会牺牲一定的分类准确率。
3.3 朴素贝叶斯算法
假设输入空间![]() 为n维向量的集合,输出空间为类标签集合
为n维向量的集合,输出空间为类标签集合![]() 。输入为特征向量
。输入为特征向量![]() ,输出为类标签
,输出为类标签![]() .X是定义在输入空间
.X是定义在输入空间![]() 上的随机变量,Y是定义在输出空间
上的随机变量,Y是定义在输出空间![]() 上的随机变量。
上的随机变量。![]() 是X和Y的联合概率密度。训练数据集
是X和Y的联合概率密度。训练数据集![]() 由
由![]() 独立同分布产生。
独立同分布产生。
朴素贝叶斯通过训练数据集学习联合概率分布![]() 。具体地,学习先验概率分布和条件概率分布。先验概率分布:
。具体地,学习先验概率分布和条件概率分布。先验概率分布:
![]() ……(3.3)
……(3.3)
条件概率分布:
![]() ……(3.4)
……(3.4)
![]() 表示第j个特征。由(3.3)和(3.4)式我们可以求得联合概率分布
表示第j个特征。由(3.3)和(3.4)式我们可以求得联合概率分布![]() 。
。
事实上,条件概率分布![]() 有指数量级的参数,其估计是不可行的。因为假设
有指数量级的参数,其估计是不可行的。因为假设![]() 可取值有
可取值有![]() 个,
个,![]() ,Y可取值有K个,那么参数个数为
,Y可取值有K个,那么参数个数为![]() 个。
个。
朴素贝叶斯法对条件概率分布作了条件独立性的假设。 由于这是一个较强的假设, 朴素贝叶斯法也由此得名。 具体地, 条件独立性假设是:
在运用朴素贝叶斯法进行分类时,对于给定的输入数据x,通过学习的模型根据贝叶斯定理计算后验概率:
将(3.5)式带入(3.6)式可得:
这就是朴素贝叶斯法进行分类的基本公式,于是,朴素贝叶斯分类器可表示为:
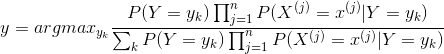 ……(3.8)
……(3.8)
其实(3.8)式中的分母对于每一类![]() 都是相同的,也就是这里的分母可看做一个标量因子,我们要求得后验概率
都是相同的,也就是这里的分母可看做一个标量因子,我们要求得后验概率![]() 主要是由先验概率和似然函数的乘积所决定的。所以(3.8)式等价于:
主要是由先验概率和似然函数的乘积所决定的。所以(3.8)式等价于:
假如我们采用极大似然估计先验概率分布和条件概率分布。先验概率![]() 的极大似然估计是:
的极大似然估计是:
设第j个特征![]() 可能取值的集合为
可能取值的集合为![]() ,条件概率
,条件概率![]() 的极大似然估计是:
的极大似然估计是:
式中,![]() 是第i个样本的第j个特征;
是第i个样本的第j个特征;![]() 是第j个特征可能取得第l个值;I为指示函数。
是第j个特征可能取得第l个值;I为指示函数。
证明暂略。
朴素贝叶斯算法:
训练数据集![]() ,其中
,其中![]() ,
,![]() 是第i个样本的第j个特征
是第i个样本的第j个特征![]() ,
,![]() 是第j个特征可能取得第l个值。
是第j个特征可能取得第l个值。
输出:实例x的分类。
(1)根据(3.10)和(3.11)式计算先验概率及条件概率;
(2)对于给定的实例![]() ,计算
,计算
(3)根据(3,9)式确定实例x的类。
3.4 朴素贝叶斯算法的实现
我们将在本部分基于贝叶斯定理与特征条件独立假设使用iris数据集进行分类,利用Python实验的模型为高斯模型,也就是假定属性/特征服从正态分布的。(除此之外,常见的模型还有:多项式模型,伯努利模型)
1、首先引入必要的包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
import math2、利用sklearn库直接加载iris数据,并做简要的数据处理
# data
def create_data():
# 利用sklearn库中的load_iris()方法,加载数据
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
# iloc使用数字来索引数据
data = np.array(df.iloc[:100, :])
# print(data)
return data[:,:-1], data[:,-1]3、划分数据集:训练集和测试集
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)4、将特征取值的可能性假设为高斯。概率密度函数为:
利用高斯的概率密度函数分布求出数学期望和标准差,之后计算条件分布的概率,再利用似然函数求出最有可能的类别,将这一整套的过程封装到类当中:
class NaiveBayes:
def __init__(self):
self.model = None
# 数学期望
@staticmethod
def mean(X):
return sum(X) / float(len(X))
# 标准差(方差)
def stdev(self, X):
avg = self.mean(X)
return math.sqrt(sum([pow(x-avg, 2) for x in X]) / float(len(X)))
# 概率密度函数
def gaussian_probability(self, x, mean, stdev):
exponent = math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
return (1 / (math.sqrt(2*math.pi) * stdev)) * exponent
# 处理X_train
def summarize(self, train_data):
summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
return summaries
# 分类别求出数学期望和标准差
def fit(self, X, y):
labels = list(set(y))
data = {label:[] for label in labels}
for f, label in zip(X, y):
data[label].append(f)
self.model = {label: self.summarize(value) for label, value in data.items()}
return 'gaussianNB train done!'
# 计算概率
def calculate_probabilities(self, input_data):
# summaries:{0.0: [(5.0, 0.37),(3.42, 0.40)], 1.0: [(5.8, 0.449),(2.7, 0.27)]}
# input_data:[1.1, 2.2]
probabilities = {}
for label, value in self.model.items():
probabilities[label] = 1
for i in range(len(value)):
mean, stdev = value[i]
probabilities[label] *= self.gaussian_probability(input_data[i], mean, stdev)
return probabilities
# 类别
def predict(self, X_test):
# {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
label = sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1])[-1][0]
return label
def score(self, X_test, y_test):
right = 0
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right += 1
return right / float(len(X_test))5、训练模型
model = NaiveBayes()
model.fit(X_train, y_train)6、预测
print(model.predict([4.4, 3.2, 1.3, 0.2]))预测结果为:0.0
7、模型测试或模型评估
model.score(X_test, y_test)评估结果得分1.0。
当然,上述实现过程是我们自己写的过程,我们其实可以直接调取sklearn的naive_bayes包下面的各种包来实现朴素贝叶斯不同模型的方法。
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score
from sklearn import datasets
iris = datasets.load_iris()
gnb = GaussianNB()
scores=cross_val_score(gnb, iris.data, iris.target, cv=10)
print("Accuracy:%.3f"%scores.mean())
输出: Accuracy:0.953。
还可以引入不同的包实现其他模型:
from sklearn.naive_bayes import BernoulliNB, MultinomialNB # 伯努利模型和多项式模型3.5 生成模型的总结
1、生成模型的求解形式:求解联合分布,再利用联合分布求解条件概率分布。
2、生成模型的求解思路:求解联合分布转化为求解类别先验概率和类别条件概率。
4、判别模型和生成模型的特点
4.1 判别模型的特点
- 判别方法寻找不同类别之间的最优分类面,反映的是异类数据之间的差异;
- 判别方法利用了训练数据的类别标识信息,直接学习的是条件概率P(Y|X)或者决策函数f(X),直接面对预测,往往学习的准确率更高;
- 由于直接学习条件概率P(Y|X)或者决策函数f(X),可以对数据进行各种程度上的抽象、定义特征并使用特征,因此可以简化学习问题。
- 缺点是不能反映训练数据本身的特性
4.2 生成模型的特点
- 从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度;
- 生成方法还原出联合概率分布,而判别方法不能;
- 生成方法的学习收敛速度更快、即当样本容量增加的时候,学到的模型可以更快地收敛于真实模型;
- 当存在隐变量时,仍可以用生成方法学习,此时判别方法不能用,比如混合高斯模型就是含有隐变量的生成方法。
- 天下没有免费午餐,联合分布是能提供更多的信息,但也需要更多的样本和更多计算,尤其是为了更准确估计类别条件分布,需要增加样本的数目,而且类别条件概率的许多信息是我们做分类用不到,因而如果我们只需要做分类任务,就浪费了计算资源。
- 另外,实践中分类问题多数情况下判别模型效果更好。

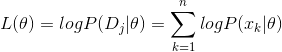


![L(\theta )=\frac{1}{n}\sum_{k=1}^{n}log P(x_{k}|\theta )=E_{x\sim D_{j}}\left [ log P(x_{k}|\theta ) \right ]=E_{x\sim D_{j}}\left [ log P_{\theta }(x_{k}) \right ]](http://img.e-com-net.com/image/info8/e16aaf5c62a5436caf6d80c7edefcc68.gif)