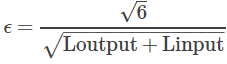[机器学习] Coursera ML笔记 - 神经网络(Learning)
引言
机器学习栏目记录我在学习Machine Learning过程的一些心得笔记,涵盖线性回归、逻辑回归、Softmax回归、神经网络和SVM等等,主要学习资料来自Standford Andrew Ng老师在Coursera的教程以及UFLDL Tutorial,同时也参考了大量网上的相关资料(在后面列出)。
本文主要记录我在学习神经网络过程中的心得笔记,共分为三个部分:
Neural network - Representation:神经网络的模型描述;
Neural network - Learning:神经网络的模型训练;
Neural network - Code:神经网络的代码实现。
前言
在本文中,我们将神经网络看作是一个分类算法,其输出是样本属于某类别的概率值 P(y==k|x;Θ),暂时不去考虑深度学习中用于特征学习的复杂卷积神经网络。因此,本文将按照一个分类模型的维度去安排文章结构,包括模型结构及数学描述、模型训练等,记录我在学习神经网络过程中的心得和思考。
本文是我在学习神经网络模型训练(Learning)时的笔记,主要以Andrew Ng老师在Coursera课程中以及UFLDL Tutorial中的关于神经网络模型训练的资料为主,文章小节安排如下:
1)神经网络的背景
2)代价函数(cost function)
3)优化(Optimization)/模型训练/参数学习
4)梯度检查(Gradient Checking)
5)随机初始化(Random Initialization)
6)Putting It Together
7)参考资料
8)结语
在阅读这部分笔记之前,请先阅读《Neural network - Representation:神经网络的模型描述》这一篇笔记,以了解神经网络的模型描述,激活函数,前向传播等基础知识。
《Neural network - Representation:神经网络的模型描述》
神经网络的背景
这里重复一遍神经网络的灵感来源,
实验证明大脑利用同一个学习算法实现了听觉、视觉等等所有的功能,这也是神经网络算法美好的愿景。
我认为一个好的算法,是具备自我学习、成长和进步能力的,可以不断的适应问题和环境变化。同样,一个好的人,一个好的公司,一个好的国家,也应该是具备这样的自我成长性,所谓好的事物是长出来的。
记得听过一个讲座,主讲人是国外大学的一位教授,他说:Deeplearning就是入侵其他领域的强有力武器,我们课题组是做图像的,半年前还一点都不懂 Natural language processing,但半年后我们就在该领域的顶级会议发了paper,因为我们只需要关心Raw data和深度网络模型,至于分词等技术我们并没有什么工作。
这位教授说的话也许有一定夸张成分,但也说明了神经网络是极具潜力的机器学习模型,可以用一套技术解决多个领域的问题,是不是非常类似于前述的人脑工作机制?并且现在大家也可以看到,深度神经网络目前基本上一统江湖,正在逐项碾压其他机器学习技术。
这是好事,也是坏事。
代价函数(cost function)
神经网络模型的代价函数取决于输出层是什么,也就是说不同的应用场景对应不同的代价函数,那么进一步的求导计算也就会有差异。
例如,在Autoencoder网络中,输出层等于输入层,此时采用均方误差(MSE)函数作为代价函数;在分类问题中,如果输出层采用Softmax回归进行分类,则可以直接采用Softmax回归的代价函数作为整个神经网络的代价函数。如果输出层采用Logistic regression进行分类,那么输出层其实就是K个Logistic regression,整个网络的代价函数就是这K个Logistic regression模型代价函数的加和。
1)输出层采用Logistic Regression
其实只要理解Cost function反映的就是预测值与实际值的误差,那么完全可以根据问题自定义一个Cost function表达式。在Coursera Machine Learning课程中将神经网络看作是输出层采用逻辑回归的分类器,因此其代价函数如下:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第1张图片](http://img.e-com-net.com/image/info8/116581347c7f4524ac433f03d2d9152f.png)
对比Logistic regression:

分析可以看出,
此时,神经网络里使用的代价函数是逻辑回归里中代价函数的一般化形式(generalization),也就是神经网络中不再是仅有一个逻辑回归输出单元,而是K个(就好像K个逻辑回归模型并行计算,也就是逻辑回归中的多分类问题)。
2)输出层采用Softmax Regression
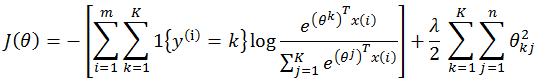
其中,
θ 指的是Softmax Regression的参数矩阵。
3)Autoencoder(输出层=输入层)
自编码神经网络是一种无监督学习算法,学习一个 Hw,b (x) ≈ x 的函数。换句话说,它尝试逼近一个恒等函数,从而使得输出接近于输入。此时,自编码神经网络采用均方误差(MSE)作为代价函数,其代价函数形式如下:

实际上,
Autoencoder并不是用于分类,而是用于学习输入数据的压缩表示,可以发现输入数据中隐含着的一些特定结构。具体可以参考:Autoencoders and Sparsity
讨论:
1)代价函数的均值化问题
这里均值化指的是代价函数是否除以样本数,以及代价函数中哪一项应该除以样本数的问题。
首先对比Coursera ML课程中神经网络的代价函数公式:

细心的同学可以看到,
这里正则化项是除以样本数 m 的,而我给出的代价函数是没有除以样本数的,如下:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第2张图片](http://img.e-com-net.com/image/info8/f8139628833f4a2aa0c22d2722807404.png)
对于正则项是否除以样本数这个问题,我作为初学者还没有看到确切深入的讨论,并且看到的大多数资料中是没有均值化的。根据实验,在不同的问题中,正则项是否均值化对优化过程的影响也不一样的,有时候可能没有影响,有时候就会致使梯度无法收敛,这一点大家可以在代码中实验一下。
通过引入正则项是否均值化问题,我想讨论的其实是:代价函数是否除以样本数(均值化)?哪一项应该除以样本数?
这里我根据学习和实验中粗浅的经验总结如下:
其实代价函数是否除以样本数(均值化),是整体均值化?还是部分均值化?这在很多算法模型中都存在这个问题,比如在Sparse Autoencoder中,代价函数由误差项,权重衰减项(正则化项),稀疏惩罚项构成,如下:
Cost function = Error term + Sparsity penalty term + Weight decay term
那么,在具体实现时,到底应该如何均值化呢?
基本原则是这样,
如果某个term与整个训练样本集有关,那么就应该均值化(除以样本数),否则就不均值化。例如Sparse Autoencoder的代价函数,误差项是所有训练样本误差的总和,稀疏惩罚项是对所有样本的稀疏性惩罚,因此这两项应该均值化,而权重衰减项是针对参数的,所以不应该均值化。
2)什么时候采用逻辑回归作为分类?什么时候采用Softmax回归呢?
这里引用UFLDL的讲解:
Softmax Regression vs. k Binary Classifiers
如果你在开发一个音乐分类的应用,需要对k种类型的音乐进行识别,那么是选择使用 softmax 分类器呢,还是使用 logistic 回归算法建立 k 个独立的二元分类器呢?
这一选择取决于你的类别之间是否互斥,例如,如果你有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么你可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时你应该使用类别数 k = 4 的softmax回归。(如果在你的数据集中,有的歌曲不属于以上四类的其中任何一类,那么你可以添加一个“其他类”,并将类别数 k 设为5。)
现在我们来看一个计算视觉领域的例子,你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是:室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢? (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片,你又会选择 softmax 回归还是多个 logistic 回归分类器呢?
在第一个例子中,三个类别是互斥的,因此更适于选择softmax回归分类器 。而在第二个例子中,建立三个独立的logistic回归分类器更加合适。
3)是否惩罚偏置单元对应的参数?
当设置偏置单元=1,并在参数矩阵 Θ 中设置第 0 列对应为偏置单元的参数时,就存在一个问题:是否惩罚偏置单元对应的参数?
引用Andrew Ng老师对该问题的说明:
不应该把这些项加入到正规化项里去,因为我们并不想正规化这些项,但这只是一个合理的规定,即使我们真的把他们加进去了,也就是 i 从0 加到s(l),这个式子(代价函数)依然成立,并且不会有大的差异。这个“不把偏差项正规化”的规定可能只是更常见一些。
一般来说是不惩罚偏置项的,因为没什么意义。
补充:
1)均方误差
均方误差(MeanSquaredError,MSE)是衡量“平均误差”的一种较方便的方法,可以评价数据的变化程度。对于等精度测量来说,还有一种更好的表示误差的方法,就是标准误差。标准误差定义为各测量值误差的平方和的平均值的平方根。数理统计中均方误差是指参数估计值与参数真值之差平方的期望值,记为MSE。MSE是衡量“平均误差”的一种较方便的方法,MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。与此相对应的,还有均方根误差RMSE、平均绝对百分误差等等。
参考:Bing网典 - 均方误差
2)标准误差
1,标准误差一般用来判定该组测量数据的可靠性,在数学上它的值等于测量值误差的平方和的平均值的平方根。
2,标准误差在正态分布中表现出正态分布曲线的陡峭程度,标准误差越小,曲线越陡峭,反之,曲线越平坦。
3,标准误差在实际的计算中使用的是标准误差估算值。
4,标准误差不是实际误差。
参考:Bing网典 - 标准误差
优化(Optimization)/模型训练/参数学习
前述已经给出了神经网络的代价函数,下面就可以通过最小化(minimize)该代价函数来求解神经网络模型的最优参数。
神经网络的优化依然可以采用梯度下降法(Gradient descent),而梯度下降法需要两方面的计算:
1)代价函数
2)梯度
即,
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第3张图片](http://img.e-com-net.com/image/info8/9ab1c21e3e3d4bcd879c9b600d716335.png)
代价函数的计算公式前面已经给出,
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第4张图片](http://img.e-com-net.com/image/info8/295edb45cbe5417c976f6b092bdc71ac.png)
J(Θ) 的梯度如何计算就需要请出大名鼎鼎的反向传播算法(Backpropagation Algorithm)!
重点:反向传播(Backpropagation)
定义如下网络,输出层采用逻辑回归:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第5张图片](http://img.e-com-net.com/image/info8/63c475515b5a4b999bbcc1643117b5fd.jpg)
首先,我们引入 符号 δ,解释如下:
![]()
代表了第 l 层的第 j 个节点的误差。
那么,各层各节点的error计算如下:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第6张图片](http://img.e-com-net.com/image/info8/cefab9004455498598495e8b035070be.png)
其中,

可以看出,与激励值(activation)计算类似,误差的计算也是层层传递的,δ3的计算依赖于δ4,δ2的计算依赖于δ3。这样一种误差计算方式,就称之为反向传播(backpropagation)。
以上面的网络模型为例,反向传播算法从后往前(或者说从右往左)计算,即从输出层开始计算,并反向逐层向前计算每一层的 δ 。反向传播法这个名字源于我们从输出层开始计算 δ 项,然后我们返回到上一层计算第 3 个隐藏层的 δ 项,接着我们再往前一步来计算 δ2。所以说我们是类似于把输出层的误差反向传播给了第3层,然后是再传到第2层,这就是反向传播的意思。
通过反向传播计算的这些 δ 项,可以非常快速的计算出所有参数的偏导数项(J(Θ) 关于 所有θ的偏导数项)。
让我们将反向传播与前向传播对比一下:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第7张图片](http://img.e-com-net.com/image/info8/54f77bfa65d849a790cdd6543b9d02f9.png)
直观地看,这个 δ 项在某种程度上捕捉到了在神经节点上的激励值的误差。反过来理解,一个神经节点的残差也表明了该节点对最终输出值的残差产生了多少影响。
因此可以说,
反向传播算法就是在逐层计算每个神经节点的激励值误差。
备注,
上面只是一种直观的解释,那么 δ 项到底是什么?其实 δ 本质上是代价函数 J 对加权和 z 的求导结果。
重点:反向传播的直观理解
这里引用Coursera ML课程中的描述:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第8张图片](http://img.e-com-net.com/image/info8/36647d0b2a2f4240b72522b24896b242.jpg)
重点:关于 δ(L) 的计算
这里重点讨论两个问题:
1)为何上面所讲的网络最后一层的 δ 与其他层计算不一致?
![]()
![]()
其实是一致的,
如前面所述,δ 本质上是代价函数 J 对加权和 z 的求导结果。这里 δ(4) 是 J 对 z(4) 的导数,δ(3) 是 J 对 z(3) 的导数,具体推导见后文。
2)在阅读资料时,为何最后一层(输出层)的 δ 有各种计算方式?
比如,
![]()
再比如,
![]()
那么是什么原因导致了上面不同的公式形式呢?其实原因就在于所采用的代价函数和输出层激励函数的形式。
不同形式的代价函数和输出层激励函数,会推导出不同的输出层误差计算公式!
下面我们可以利用两种形式的代价函数进行偏导数计算,验证上述结论,如下:
1)
Cost function采用:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第9张图片](http://img.e-com-net.com/image/info8/75f393b2ad7045479cc71ee61b319896.png)
输出层激励函数(也可以称为预测函数)采用:
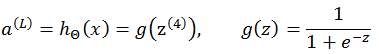
则 δ(L) 推导如下:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第10张图片](http://img.e-com-net.com/image/info8/01d1e86fb9a0472695e3885c5d30564c.png)
则 δ(L) 推导如下:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第12张图片](http://img.e-com-net.com/image/info8/753cffa09b014b2a91940939d9b33652.png)
综上可以看出,
δ(L) 的形式与代价函数 J 和输出层激励函数 g 的形式直接相关。
备注,
Andrew Ng老师在课程中为了降低理解难度,并没有讲明上述的推演关系,而是给出一种直观的解释,即:δ(L) = 实际值 - 预测值。作为入门的话,这样理解也未尝不可。
至此,完成 δ(L) 计算的推导和讨论,也解答了神经网络最后一层误差计算出现不同公式形式的原因,希望可以为大家提供一定参考。
如果对于上述推导感兴趣,请参考: https://share.coursera.org/wiki/index.php/ML:Neural_Networks:_Learning http://deeplearning.stanford.edu/wiki/index.php/Backpropagation_Algorithm
重点:梯度计算(Gradient Computation)
在神经网络模型中,代价函数 J(Θ) 关于 参数 θ 的偏导数(partial derivative terms)/梯度计算如下:
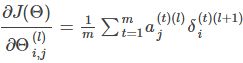
向量化描述如下:
![]()
关于该计算公式的推导可以参考wiki ML中关于Neural Network: Learning一节(https://share.coursera.org/wiki/index.php/ML:Neural_Networks:_Learning)。
Andrew Ng老师给出的用于计算梯度的Backpropagation Algorithm如下:
Backpropagation Algorithm
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第13张图片](http://img.e-com-net.com/image/info8/eb149451dfa84d13bbc0e6d02d921d7f.jpg)
写到这里想起来前阵子听讲座,主讲人的两句吐槽:
1)入门神经网络只要学会计算梯度就行了,其他什么概念都不需要了解,比SVM简单多了,并且想现在很多Toolbox连梯度都帮你计算了,你还需要做什么?你只需要配置下网络结构就可以了,代码都不用写,越来越没有门槛了。
2)算个梯度还搞出个什么反向传播(Backpropagation),说到底不就是链式法则(chain rule)么!现在人真会玩,换个名词就炒冷饭!
关于利用反向传播算法计算梯度,可以重点参考:
Backpropagation Algorithm
备注,
也许有人会有疑问,反向传播到底是用来计算梯度的?还是仅仅用来逐层计算误差的??,为何这里所写的反向传播只计算了误差,而没有计算梯度??
确实,在Coursera ML课程中,Andrew Ng老师的讲解一开始告诉你说,Backpropagation是用来反向逐层计算误差的。而后续的讲解,包括很多资料里所描述的BP算法又是是用来计算梯度的。这到底是咋回事呢?
如前所述,反向传播仅仅是计算过程的一个直观上的称呼罢了,更重要的是其背后的神经网络求导思想,所以,
无论说:反向传播是用来逐层计算(或称传递)误差的;又或者说:反向传播是用来计算梯度的。
其实所说所指的都是如何对神经网络的参数进行快速求导这个事情。
如果非要较真儿,也许可以这样理解前向传播、反向传播、梯度计算之间的关系:
前向传播和反向传播是一种计算过程的直观描述,而梯度是基于前向传播得到的Activation和反向传播得到的Error进行计算的。
为了更清晰更方便的记忆激励值、误差、前向传播、反向传播等概念,可以这样:
前向传播计算 a,反向传播计算 δ,基于 a 和 δ 计算梯度。
重点:梯度下降(Gradient Descent)
得到代价函数和梯度,就可以利用梯度下降算法来求解最优参数,描述如下:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第14张图片](http://img.e-com-net.com/image/info8/fc9da06d49a0450f815f024ecee9b184.png)
补充:
1)梯度、偏导数、方向导数
方向导数:函数上某一点在某一方向上的导数值,偏导数就是沿着坐标轴的方向导数;
偏导数:一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化),偏导数反映的是函数沿坐标轴正方向的变化率;
梯度:梯度即是某一点最大的方向导数,沿梯度方向函数有最大的变化率(正向增加,逆向减少);
参考:
方向导数和梯度
http://blog.csdn.net/wolenski/article/details/8030654
百度百科-梯度
http://baike.baidu.com/subview/454441/12503183.htm
梯度检查(Gradient Checking)
反向传播算法作为一个有很多细节的算法在实现的时候比较复杂,可能会遇到很多细小的错误。所以如果把BP算法和梯度下降法或者其他优化算法一起运行时,可能看起来运行正常,并且代价函数可能在每次梯度下降法迭代时都会减小,但是可能最后得到的计算结果误差较高,更要命的是很难判断这个错误结果是哪些小错误导致的。
解决该问题的方法是:梯度检查 (Gradient Checking)
梯度检查 (Gradient Checking)的思想就是通过数值近似(numerically approximately)的方式计算导数近似值,从而检查导数计算是否正确。虽然数值计算方法速度很慢,但实现起来很容易,并且易于理解,所以它可以用来验证例如BP算法等快速求导算法的正确性。
如前所述,机器学习中大部分算法的核心就是代价值计算和梯度计算,因此,在实现神经网络或者其他比较复杂的模型时候,利用Gradient Checking可以检查算法是否正确实现。
梯度检查 (Gradient Checking)的核心是导数的数值计算,公式如下:

多参数情况的公式如下:

梯度检查 (Gradient Checking)的实现,
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第15张图片](http://img.e-com-net.com/image/info8/49f7a96b1efa41458cf5fb8846ff5f5d.png)
其中,
DVec:利用反向传播算法得到的导数,BP是一个比较有效率的计算导数的方法;
gradApprox:利用数值近似得到的导数,数值计算法速度很慢;
如果两者相等或者近似,最多几位小数的差距,那么就可以确信所实现的BP算法是正确的。
随机初始化(Random Initialization)
当运行一个优化算法(例如梯度下降算法或者其他高级优化算法)时,需要给变量 θ 设置初始值。例如,在梯度下降法中,需要对 θ 进行初始化(通常为全0),然后使用梯度下降的方法不断最小化函数 J,最终代价函数 J 下降到最小。
但要注意的是,
将 θ 初始化为全 0 向量在逻辑回归时是可行的的,但在训练神经网络时是不可行的,这会使得神经网络无法学习出有价值的信息。
以第一层参数矩阵(权重矩阵)为例,假定有K个隐藏单元,那么神经网络的参数矩阵 Θ1 实质上对应着特征的K个映射函数(映射关系),如果参数全为 0,那就意味着所有映射关系都是相同的,即所有的隐藏单元都在计算相同的激励值,那么这样一个具有很多隐藏单元的网络结构就是完全多余的表达,最终该网络只能学到一种特征。
这种现象称为:对称权重(Symmetric ways)
解决办法其实很简单,即:随机初始化(Random Initialization)
描述如下:

所有权重相同的问题称为对称权重(Symmetric ways),随机初始化解决的就是如何打破这种对称性,需要做的就是对 θ 的每个值进行初始化,使其范围在 -ɛ 到 +ɛ 之间。
Θ 的初始化:
![]()
Putting It Together
上面已经讲解了神经网络训练的各个部分,综合起来就可以得到一个最基础神经网络学习算法的实现过程。
训练一个神经网络算法模型,第一件事就是设计网络结构,也就是搭建网络的大体框架(architecture),框架的意思是神经元之间的连接模式,包括,
· 网络层数,主要是隐层数量;
· 每一层的节点个数,主要是隐藏单元数量;
这里引用课程中的一张PPT来作说明:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第16张图片](http://img.e-com-net.com/image/info8/656c9b59812a4d598a935aeb4b662612.jpg)
下面总结网络结构设计的几点基本原则:
网络结构的选择规则:
神经网络搭建时,可能会从上面PPT中所示的几种结构中选择,一个默认的规则是只使用单个隐藏层,即PPT中最左边的结构,或者如果使用不止一个隐藏层的话,同样也有一个默认规则就是每一个隐藏层通常都应有相同的隐藏单元数。
通常来说,PPT中左边这个结构是较为合理的默认结构。
输入层与输出层:
对于一个用于分类的神经网络,输入层即特征,输出层即类别。
Number of input units = dimension of features x(i)
Number of output units = number of classes
隐藏单元的选择规则:
通常情况下隐藏单元越多越好,不过需要注意的是如果有大量隐藏单元,那么计算量一般会比较大。一般来说,每个隐藏层所包含的单元数量还应该和输入 x 的维度相匹配,也要和特征的数目匹配。
可能隐藏单元的数目和输入特征的数量相同,或者是它的二倍或者三倍、四倍。一般来说,隐藏单元的数目取为稍大于输入特征数目都是可以接受的。
完成上述理解,便可以得到神经网络的训练过程,如下。
神经网络的训练过程:
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第17张图片](http://img.e-com-net.com/image/info8/0d094d43e13e4d75a4c01271e1ae0e1b.png)
下面附一张Andrew Ng老师在Coursera ML课程中的PPT,来给出神经网络训练过程的直观描述:
(由于绘图所限,这里假定代价函数 J(Θ) 只有两个参数值)
![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第18张图片](http://img.e-com-net.com/image/info8/f6c803ecae0844a0b6c517641a83d9a1.jpg)
说明:
神经网络的代价函数J(θ)是一个非凸函数,因此理论上是只能够停留在局部最小值的位置。
———————————————————————
实际上,梯度下降算法和其他一些高级优化方法理论上都只能使神经网络的代价函数收敛于局部最小值,不过一般来讲这个问题并不是什么要紧的事,因为尽管不能保证这些优化算法一定会得到全局最优值,但通常来讲这些算法在最小化代价函数 J(θ) 的过程中还是表现得很不错的,通常能够得到一个很小的局部最小值,虽然这不一定是全局最优值。
参考资料
UFLDL Tutorial
http://ufldl.stanford.edu/tutorial/
Coursera - Machine learning( Andrew Ng)
https://www.coursera.org/learn/machine-learning
Coursera -ML:Neural Networks: Representation
https://share.coursera.org/wiki/index.php/ML:Neural_Networks:_Representation
Coursera -ML:Neural Networks: Learning
https://share.coursera.org/wiki/index.php/ML:Neural_Networks:_Learning
结语
以上就是神经网络模型Learning的相关知识点和实现过程,其中重点讨论了神经网络的代价函数模型和参数学习中的Backpropagation算法,这也是我在学习NN时反复理解了好久的问题,希望可以为大家提供一些帮助,也欢迎交流讨论,谢谢!
本文的文字、公式和图形都是笔者根据所学所看的资料经过思考后认真整理和撰写编制的,如有朋友转载,希望可以注明出处:
[机器学习] Coursera ML笔记 - 神经网络(Learning)
http://blog.csdn.net/walilk/article/details/50504393
·
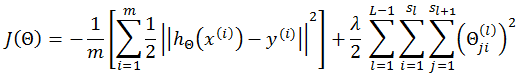

![[机器学习] Coursera ML笔记 - 神经网络(Learning)_第11张图片](http://img.e-com-net.com/image/info8/65bcc886874d4bfb9e24b8e8d55fa377.png)