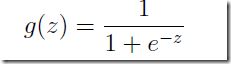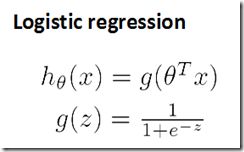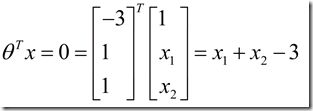Logistic Regression(逻辑回归)（二）—深入理解

（整理自AndrewNG的课件，转载请注明。整理者：华科小涛@http://www.cnblogs.com/hust-ghtao/）

 

    上一篇讲解了Logistic Regression的基础知识，感觉有很多知识没说清楚，自己理解的也不透彻，好在coursera上NG又从另外的角度讲了一下。这里我权当个搬运工，把他讲的搬过来，加上自己的理解整理一下。主要分成三个部分：对的再理解、Decision Boundary(决策边界)、多类问题。

 

1 对的再理解

 

    这部分采用启发式的方式来讲解，循序渐进的在跟大家讲一下选择的合理性。我们知道Linear Regression不适合用来解决分类问题，从下面角度来理解：

    对于Logistic Regression，

 

   

 

    ，由图显然，若x从负无穷到正无穷变化时，的变化范围也是从负无穷到正无穷，而y的取值只能是0或1 。这岂不是很奇怪，直观想象：即使不能映射到0或1，也至少将映射到，数学里还真有一个函数，那就是我们上次提到的：

 

  

 

    那直接将特征x从映射到可以吗？显然不合理，若是那样：当x大于0时，就判断为1类，否则为0类，显然不符合实际情况，应该具体问题具体分析。所以就将进行映射，对于分类问题，通过恰当的选择特征构造，通过梯度下降法，是可以训练出分类器的。

    从概率上这也是合理的，计算出的是，对于输入x，输出y=1的概率。假如对于输入x，计算出=0.7，则表示y=1的概率为70%，则判断为y=1 。

 

2 Decision Boundary(决策边界)

    上面介绍了分类，却没对的含义，给出形象的解释：

   

 

图示如下：

 

   

 

假如已经训练好分类器为，我们对新输入x，判断其类别的依据是：

 

    ，由于，所以等价于判断：

 

   

   

    所以就是我们的分类面，即Decision Boundary 。举例说明：

 

    ，对于这个分类问题有两个特征和。我们假设，经过训练求解：

 

，则分界面为

 

，即

 

  。

 

    再来看一个非线性决策边界的例子：

 

    ，对于这个分类问题有4个特征，分别是，，和。我们假设，经过训练求解：

 

    ，则分界面的方程为： ，为一个圆，图如下：

 

    。

   

    也就是说，虽然罗辑回归的假设函数为，但分类结果的直观表示却是，即Decision Boundary(决策边界)。

 

3 多类问题

    以上我们主要介绍了用逻辑回归解决二值分类的问题，下面我们简要介绍一下多类问题。现实生活中有很多的多类问题，例如要根据掌握的信息进行天气的预测，就有阴、晴、雨、雪等情况；对邮件进行分类管理，也可分为家人、朋友、同事等管理类别。

    用Logistic Regression解决多类问题的思路很简单：就是把就绝K类的问题，转化为求解K的二值分类问题。下面以一个例子来说明：

 

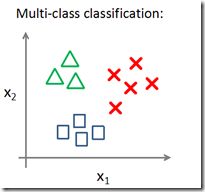    ，这是一个简单的3类问题，我们把它分解成下面3个二值问题来解决：

 

 

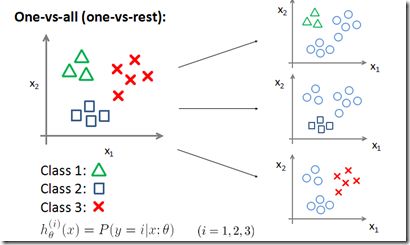，经过这样的处理就把问题转换成已知的二值分类问题了，用逻辑回归分别进行求解：

 

就可以得到，表示对于输入变量x，它属于i类的概率。如果要对新来的输入进行类别的预测，分别计算，那类对应的最大，说明输入属于这个类别的概率最大，就判断为这个类别。

    这里有一点需要注意：对于K类的多类问题，是要分解成K个二值问题的，而不是（K-1）个或更少。因为各个之间没有什么直接的关系（之和不为1）：

 

，可以看到它们之间有交叉，也有都不包含的区域。

转载于:https://www.cnblogs.com/hust-ghtao/p/3684346.html