YOLO V4读书笔记

分享几个相关链接

paper链接
code链接
ppt链接 可能需要外网，但真的很好用！出不去可以用网盘下
网盘链接 提取码：j25i

背景

之前用yolo v3做过救生衣检测，但实际应用效果不太好。后面数据集增加后，并且数据增强了一波，发现效果还是可以的，并且速度也很快。这次四月份出了yolo v4,整体感觉就是把19年新出的几个算法融合了进去。
例如Mix-UP，Cut-Mix，Mosaic算法，就是对多张图像进行处理，对其目标物进行融合、替换或者遮挡，可以增加训练的效果，一张包含四种内容，同时基于之前的实验结论（小物体在loss中占比很小，不到总loss的0.1，说明模型对小物体的网络监督是不足的），可以提交小物体的准确率。

目的

设计一个速度快，易部署，且训练简单的目标检测算法

亮点

• 开发了一个简单且高效的目标检测算法 （YOLOV4），该算法可通过普通的GPU（1080TI或者2080Ti）来训练。
• 作者验证了在目标检测算法训练过程中不同的技巧tricks对实验性能的影响，这些tricks主要包括Bag-ofFreebies和Bag-of-Specials。
• 作者修改了一些state-of-the-art(SOTA)的算法，使得这些算法适用于单GPU上训练，这些算法包括了CBN，PAN和SAM等等。
  
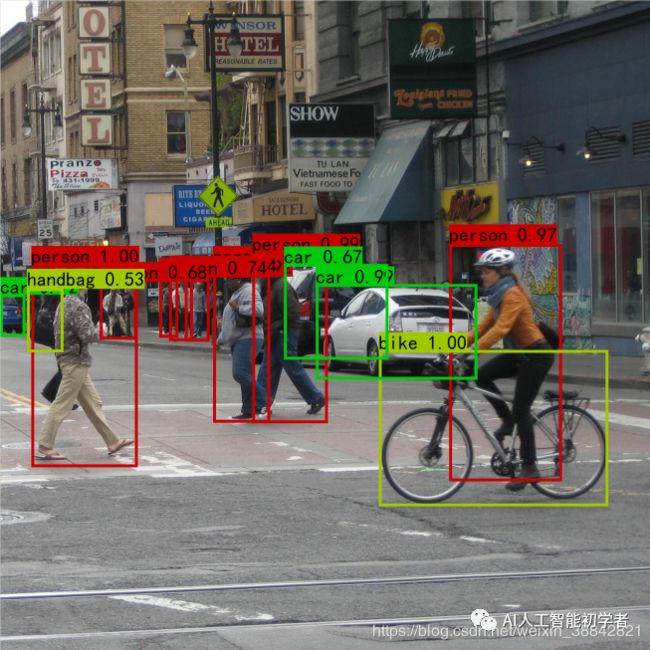
  由上图可以看出，在yolov3 的基础上，yolov4的mAP最高可以达到44%，而且保证速度快。
  给我的感觉就是yolov4的整体检测思路相差不大，但是每个特征层的训练网络都发生了变化。
  YOLOV4改进的部分（不完全）
  1、主干特征提取网络：DarkNet53 => CSPDarkNet53
  2、特征金字塔：SPP，PAN
  3、分类回归层：YOLOv3（未改变）
  4、训练用到的小技巧：Mosaic数据增强、Label Smoothing平滑、CIOU、学习率余弦退火衰减
  5、激活函数：使用Mish激活函数
  以上并非全部的改进部分，还存在一些其它的改进，由于YOLOV4使用的改进实在太多了，很难完全实现与列出来，这里只列出来了一些我比较感兴趣，而且非常有效的改进。

目标检测构建

Object detection = Backbone + Neck + Head

Backbone:主干网络的意思，代表这个网络的深度，决定了最终结果的好坏。用于提取特征，即提取图片中的信息，供后面的网络使用。通常使用别人设计好的网络，例如resnet，ResNeXt等，该层网络一般用官方训练好的网络来提取特征。，后面接着我们自己的网络。让网络的这两个部分同时进行训练，因为加载的Backbone模型已经具有提取特征的能力了，在我们的训练过程中，会对他进行微调，使得其更适合于我们自己的任务。

head：head是获取网络输出内容的网络，利用之前提取的特征，head利用这些特征，做出预测。

neck:是放在backbone和head之间的，是为了更好的利用backbone提取的特征

bottleneck:瓶颈的意思，通常指的是网网络输入的数据维度和输出的维度不同，输出的维度比输入的小了许多，就像脖子一样，变细了。经常设置的参数 bottle_num=256，指的是网络输出的数据的维度是256 ，可是输入进来的可能是1024维度的。

GAP：在设计的网络中经常能够看到gap这个层，我之前不知道是干啥的，后了解了，就是Global Average Pool全局平均池化，就是将某个通道的特征取平均值，经常使用AdaptativeAvgpoold(1),在pytorch中，这个代表自适应性全局平均池化，说人话就是将某个通道的特征取平均值。

Embedding: 深度学习方法都是利用使用线性和非线性转换对复杂的数据进行自动特征抽取，并将特征表示为“向量”（vector），这一过程一般也称为“嵌入”（embedding）

常用的汇总|目标检测中的数据增强、backbone、head、neck、损失函数
 

Mosaic算法

Yolov4的mosaic 数据增强是参考CutMix数据增强，理论上类似，CutMix的理论可以参考这篇CutMix，但是mosaic利用了四张图片，使得mini-batch大小不需要很大，那么一个GPU就可以达到比较好的效果。
分别对四张图片进行翻转、缩放、色域变化等，并且按照四个方向位置摆好,之后进行图片的组合和框的组合。
从数据上动手，保证训练模型可以拥有足够复杂的训练量，将背景和物体的检测效果更加精确，同时训练效率更加高效。
根据论文所说其拥有一个巨大的优点是丰富检测物体的背景！且在BN计算的时候一下子会计算四张图片的数据！
代码链接
github

def rand(a=0, b=1):
    return np.random.rand()*(b-a) + a

def merge_bboxes(bboxes, cutx, cuty):

    merge_bbox = []
    for i in range(len(bboxes)):
        for box in bboxes[i]:
            tmp_box = []
            x1,y1,x2,y2 = box[0], box[1], box[2], box[3]

            if i == 0:
                if y1 > cuty or x1 > cutx:
                    continue
                if y2 >= cuty and y1 <= cuty:
                    y2 = cuty
                    if y2-y1 < 5:
                        continue
                if x2 >= cutx and x1 <= cutx:
                    x2 = cutx
                    if x2-x1 < 5:
                        continue

            if i == 1:
                if y2 < cuty or x1 > cutx:
                    continue

                if y2 >= cuty and y1 <= cuty:
                    y1 = cuty
                    if y2-y1 < 5:
                        continue

                if x2 >= cutx and x1 <= cutx:
                    x2 = cutx
                    if x2-x1 < 5:
                        continue

            if i == 2:
                if y2 < cuty or x2 < cutx:
                    continue

                if y2 >= cuty and y1 <= cuty:
                    y1 = cuty
                    if y2-y1 < 5:
                        continue

                if x2 >= cutx and x1 <= cutx:
                    x1 = cutx
                    if x2-x1 < 5:
                        continue

            if i == 3:
                if y1 > cuty or x2 < cutx:
                    continue

                if y2 >= cuty and y1 <= cuty:
                    y2 = cuty
                    if y2-y1 < 5:
                        continue

                if x2 >= cutx and x1 <= cutx:
                    x1 = cutx
                    if x2-x1 < 5:
                        continue

            tmp_box.append(x1)
            tmp_box.append(y1)
            tmp_box.append(x2)
            tmp_box.append(y2)
            tmp_box.append(box[-1])
            merge_bbox.append(tmp_box)
    return merge_bbox

def get_random_data(annotation_line, input_shape, random=True, hue=.1, sat=1.5, val=1.5, proc_img=True):
    '''random preprocessing for real-time data augmentation'''
    h, w = input_shape
    min_offset_x = 0.4
    min_offset_y = 0.4
    scale_low = 1-min(min_offset_x,min_offset_y)
    scale_high = scale_low+0.2

    image_datas = [] 
    box_datas = []
    index = 0

    place_x = [0,0,int(w*min_offset_x),int(w*min_offset_x)]
    place_y = [0,int(h*min_offset_y),int(w*min_offset_y),0]
    for line in annotation_line:
        # 每一行进行分割
        line_content = line.split()
        # 打开图片
        image = Image.open(line_content[0])
        image = image.convert("RGB") 
        # 图片的大小
        iw, ih = image.size
        # 保存框的位置
        box = np.array([np.array(list(map(int,box.split(',')))) for box in line_content[1:]])

        # image.save(str(index)+".jpg")
        # 是否翻转图片
        flip = rand()<.5
        if flip and len(box)>0:
            image = image.transpose(Image.FLIP_LEFT_RIGHT)
            box[:, [0,2]] = iw - box[:, [2,0]]

        # 对输入进来的图片进行缩放
        new_ar = w/h
        scale = rand(scale_low, scale_high)
        if new_ar < 1:
            nh = int(scale*h)
            nw = int(nh*new_ar)
        else:
            nw = int(scale*w)
            nh = int(nw/new_ar)
        image = image.resize((nw,nh), Image.BICUBIC)

        # 进行色域变换
        hue = rand(-hue, hue)
        sat = rand(1, sat) if rand()<.5 else 1/rand(1, sat)
        val = rand(1, val) if rand()<.5 else 1/rand(1, val)
        x = rgb_to_hsv(np.array(image)/255.)
        x[..., 0] += hue
        x[..., 0][x[..., 0]>1] -= 1
        x[..., 0][x[..., 0]<0] += 1
        x[..., 1] *= sat
        x[..., 2] *= val
        x[x>1] = 1
        x[x<0] = 0
        image = hsv_to_rgb(x)

        image = Image.fromarray((image*255).astype(np.uint8))
        # 将图片进行放置，分别对应四张分割图片的位置
        dx = place_x[index]
        dy = place_y[index]
        new_image = Image.new('RGB', (w,h), (128,128,128))
        new_image.paste(image, (dx, dy))
        image_data = np.array(new_image)/255

        # Image.fromarray((image_data*255).astype(np.uint8)).save(str(index)+"distort.jpg")

        index = index + 1
        box_data = []
        # 对box进行重新处理
        if len(box)>0:
            np.random.shuffle(box)
            box[:, [0,2]] = box[:, [0,2]]*nw/iw + dx
            box[:, [1,3]] = box[:, [1,3]]*nh/ih + dy
            box[:, 0:2][box[:, 0:2]<0] = 0
            box[:, 2][box[:, 2]>w] = w
            box[:, 3][box[:, 3]>h] = h
            box_w = box[:, 2] - box[:, 0]
            box_h = box[:, 3] - box[:, 1]
            box = box[np.logical_and(box_w>1, box_h>1)]
            box_data = np.zeros((len(box),5))
            box_data[:len(box)] = box

        image_datas.append(image_data)
        box_datas.append(box_data)

        img = Image.fromarray((image_data*255).astype(np.uint8))
        for j in range(len(box_data)):
            thickness = 3
            left, top, right, bottom  = box_data[j][0:4]
            draw = ImageDraw.Draw(img)
            for i in range(thickness):
                draw.rectangle([left + i, top + i, right - i, bottom - i],outline=(255,255,255))
        img.show()


    # 将图片分割，放在一起
    cutx = np.random.randint(int(w*min_offset_x), int(w*(1 - min_offset_x)))
    cuty = np.random.randint(int(h*min_offset_y), int(h*(1 - min_offset_y)))

    new_image = np.zeros([h,w,3])
    new_image[:cuty, :cutx, :] = image_datas[0][:cuty, :cutx, :]
    new_image[cuty:, :cutx, :] = image_datas[1][cuty:, :cutx, :]
    new_image[cuty:, cutx:, :] = image_datas[2][cuty:, cutx:, :]
    new_image[:cuty, cutx:, :] = image_datas[3][:cuty, cutx:, :]

    # 对框进行进一步的处理
    new_boxes = merge_bboxes(box_datas, cutx, cuty)

    return new_image, new_boxes

 

Mish激活函数

$$Relu(x)=max(0,x)$$
ReLU和Mish的对比，Mish的梯度更平滑

$$Mish=x\ast tanh(ln(1+e^x))$$

为什么Mish表现这么好

以上无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许允许更好的梯度流，而不是像ReLU中那样的硬零边界。

最后，可能也是最重要的，目前的想法是，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。

尽管如此，我测试了许多激活函数，它们也满足了其中的许多想法，但大多数都无法执行。这里的主要区别可能是Mish函数在曲线上几乎所有点上的平滑度。

这种通过Mish激活曲线平滑性来推送信息的能力如下图所示，在本文的一个简单测试中，越来越多的层被添加到一个测试神经网络中，而没有一个统一的函数。随着层深的增加，ReLU精度迅速下降，其次是Swish。相比之下，Mish能更好地保持准确性，这可能是因为它能更好地传播信息。

Mish实验总结

ReLU有一些已知的弱点，但是通常它执行起来很轻，并且在计算上很轻。Mish具有较强的理论渊源，在测试中，就训练稳定性和准确性而言，Mish的平均性能优于ReLU。
复杂度只稍微增加了一点(V100 GPU和Mish，相对于ReLU，每epoch增加大约1秒)，考虑到训练稳定性的提高和最终精度的提高，稍微增加一点时间似乎是值得的。
最终，在今年测试了大量新的激活函数后，Mish在这方面处于领先地位，我怀疑它很有可能成为AI未来的新ReLU。

Label Smoothing平滑

对于分类问题，尤其是多类别分类问题中，常常把类别向量做成one-hot vector(独热向量)。one-hot vector 对应的向量可表示为[0, 1, 0]，即对于长度为n 的数组，只有一个元素是1，其余都为0。
对于损失函数，我们需要用预测概率去拟合真实概率，而拟合one-hot的真实概率函数会带来两个问题：

1. 无法保证模型的泛化能力，容易造成过拟合；
2. 全概率和0概率鼓励所属类别和其他类别之间的差距尽可能加大，而由梯度有界可知，这种情况很难adapt。会造成模型过于相信预测的类别。

其实Label Smoothing平滑就是将标签进行一个平滑，原始的标签是0、1，在平滑后变成0.005(如果是二分类)、0.995，也就是说对分类准确做了一点惩罚，让模型不可以分类的太准确，太准确容易过拟合。

new_onehot_labels = onehot_labels * (1 - label_smoothing) + label_smoothing / num_classes

假设我做一个蛋白质二级结构分类，是三分类，那么K=3；

假如一个真实标签是[0, 0, 1]，取epsilon = 0.1，

新标签就变成了 （1 - 0.1）× [0, 0, 1] + (0.1 / 3) = [0, 0, 0.9] + [0.0333, 0.0333, 0.0333] = [0.0333, 0.0333, 0.9333]

CIoU(Complete-IoU Loss)

由于IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值。
只是数值上的计算，对框的其他因素都没有考虑进去。例如目标物体的大小也没考虑，Iou
CIOU将目标与anchor之间的距离，重叠率、尺度以及惩罚项都考虑进去，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。而惩罚因子把预测框长宽比拟合目标框的长宽比考虑进去。
$$L_{CIoU}=1-IoU+\frac{{\rho }^2(b,b^{gt})}{c^2}+\alpha v$$

学习率余弦退火算法

余弦退火衰减法，学习率会先上升再下降，这是退火优化法的思想。（关于什么是退火算法可以百度。）
上升的时候使用线性上升，下降的时候模拟cos函数下降。执行多次。
效果如图所示：

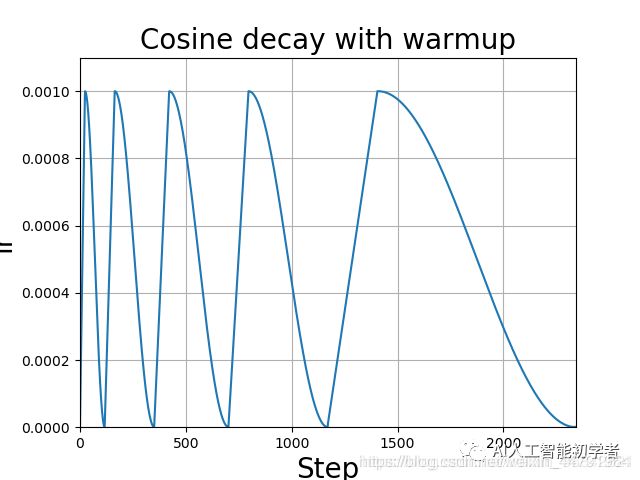
lr_scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=5, eta_min=1e-5)

backbone

在yolov3中Darknet53的结构，其由一系列残差网络结构构成。在Darknet53中，其存在resblock_body模块，其由一次下采样和多次残差结构的堆叠构成，Darknet53便是由resblock_body模块组合而成。

yolov4中对bockbone的改进点主要有两个：

• 特征提取网络：DarkNet53 => CSPDarkNet53
• Relu => Mish激活函数，例如上图中改为DarknetConv2D_BN_Mish(),效果更好，可以提供训练稳定性和最终精度，虽然稍微耗时，但是在接受范围内。
  ##CSPDarkNet53
  
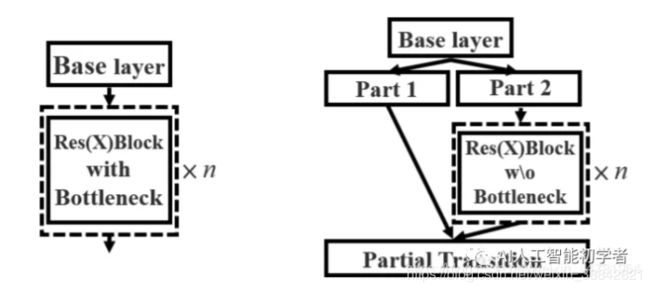
  上图左边是resblock_body的结构，通过CSPnet的结构，修改为右图。就是将原来残差块的堆叠进行两部分的拆分，分别变为以下两部分：
• 主干部分(part 2)继续进行原来的残差块的堆叠
• 另一部分(part 1)则像一个残差边一样，经过少量处理直接连接到最后

CSPnet优化了梯度反向传播路径，提升了网络的学习能力，同时在处理速度和内存方面提升了不少。在目标检测方面，也做了轻量化设计，结果很优秀。

特征金字塔

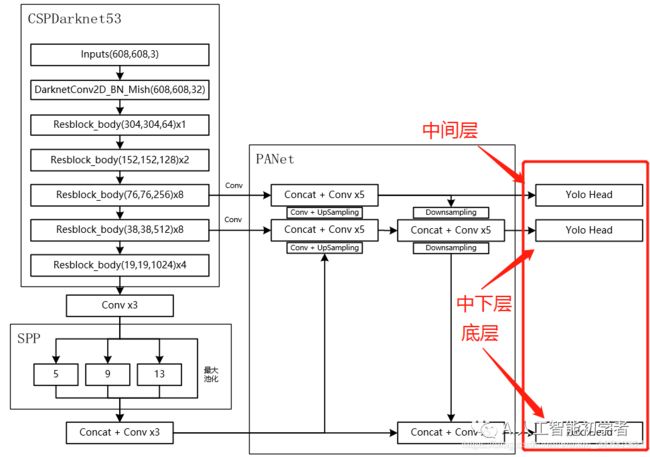
当输入是608x608时，特征结构如下：

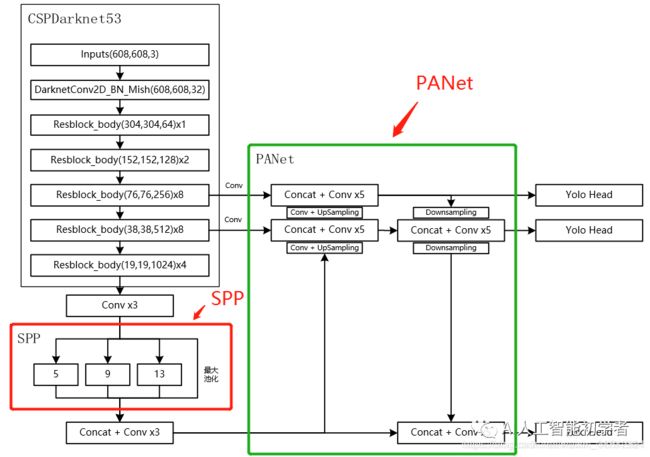
使用了SPP结构和PANet结构,分别在上图用红框和绿框标出来了。

SPP结构

CSPdarknet53的最后一个特征层的卷积处理完后，SPP结构对CSPdarknet53的最后一个特征层进行三次DarknetConv2D_BN_Leaky卷积后，分别利用四个不同尺度的最大池化进行处理，最大池化的池化核大小分别为13x13、9x9、5x5、1x1（1x1即无处理）

#---------------------------------------------------#
#   SPP结构，利用不同大小的池化核进行池化
#   池化后堆叠
#---------------------------------------------------#
class SpatialPyramidPooling(nn.Module):
    def __init__(self, pool_sizes=[5, 9, 13]):
        super(SpatialPyramidPooling, self).__init__()
        self.maxpools = nn.ModuleList([nn.MaxPool2d(pool_size, 1, pool_size//2) for pool_size in pool_sizes])

    def forward(self, x):
        features = [maxpool(x) for maxpool in self.maxpools[::-1]]
        features = torch.cat(features + [x], dim=1)

        return features

其最大作用就是它能够极大地增加感受野，分离出最显著的上下文特征。

PANet结构

PANet是2018的一种实例分割算法，其具体结构由反复提升特征的意思。

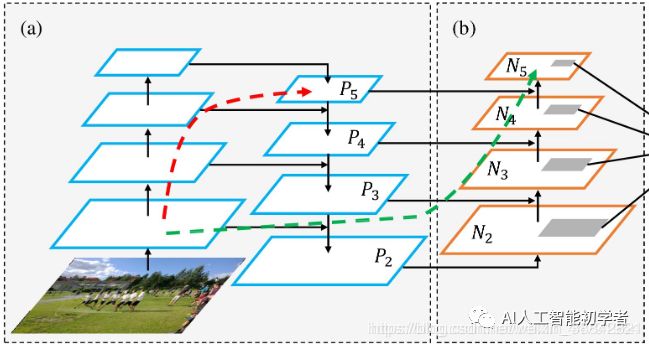
上图为原始的PANet的结构，可以看出来其具有一个非常重要的特点就是特征的反复提取。
在（a）里面是传统的特征金字塔结构(FPN)，在完成特征金字塔从下到上的特征提取后，还需要实现（b）中从上到下的特征提取。

由图可以看出，两个上采样+一个下采样，提取到了丰富的特征。

YoloHead利用获得到的特征进行预测

1. 在特征利用部分，YoloV4提取多特征层进行目标检测，一共提取三个特征层，分别位于中间层，中下层，底层，三个特征层的shape分别为(76,76,256)、(38,38,512)、(19,19,1024)。
2. 输出层的shape分别为(19,19,75)，(38,38,75)，(76,76,75)，最后一个维度为75是因为该图是基于voc数据集的，它的类为20种，YoloV4只有针对每一个特征层存在3个先验框，所以最后维度为3x25 = 75。（4+1+20）
   [x,y,w,h] + 置信度 + 分类结果
   如果使用的是coco训练集，类则为80种，最后的维度应该为255 = 3x85，三个特征层的shape为(19,19,255)，(38,38,255)，(76,76,255)

解码

1. 取出每一类得分大于self.obj_threshold的框和得分。
2. 利用框的位置和得分进行非极大抑制。

实验成果