少女Q的量化交易之路 #week3 之一

这周事情非常多，Deep learning有一个project, Machine learning 的FSA算法实现也很难（之后可能会开个新坑）。信号系统这门课也卡在跟轨迹上T_T

Leetcode Part

Leetcode Q14 Longest Common Prefix
easy- string

题目大意：输入一串字符，输出这些字符从首字母开始最长的相同字符串。如果输入为空，输出为’’。

个人思路：先找到输入的这串字符串里最短的字符的长度n，并得到下标和value。然后比较str里面每个字符串前n个字符，是否和这个value一样。如果是一样的，直接输出pre，不一样，就把n减掉1再做比较。

代码实现：

class Solution:
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        if not strs:
            return''
        short = []
        strslen = len(strs)
        for i in range(0, strslen):
            a = len(strs[i])
            short.append(a)
        sho = min(short) #最小长度
        j = short.index(min(short))#最小长度对应的下标
        pre = strs[j]# 最小长度的那个值
        for s in strs:            
            while s[0: sho] != pre:
                sho = sho -1
                pre = pre[0:sho]
            if s[0: sho] == pre:
                pre = pre 
        return pre

遇到的问题：

• if 和 while要区分使用
  本来的程序while部分是用if的，如下：

for s in strs:            
            if s[0: sho] != pre:
                sho = sho -1
                pre = pre[0:sho]
            else:
                pre = pre 
        return pre

当输入为[“flower”,“flow”,“flight”]时，输出为[’‘flo’’]，原因为if就只能做个判断，循环一次。所以当最后一次比较flight和flow时，减去一位进行比较后就直接输出了。

• list.append(obj) list.index(value)
  list一定不能再赋值给list了，不然就是none.
  找list里面value的下标可以用这个index。
• 字符串的截取

str = ‘0123456789’
print str[0:3] #截取第一位到第三位的字符
print str[:] #截取字符串的全部字符
print str[6:] #截取第七个字符到结尾
print str[:-3] #截取从头开始到倒数第三个字符之前
print str[2] #截取第三个字符
print str[-1] #截取倒数第一个字符
print str[::-1] #创造一个与原字符串顺序相反的字符串
print str[-3:-1] #截取倒数第三位与倒数第一位之前的字符
print str[-3:] #截取倒数第三位到结尾

Leetcode Q7 Reverse Integer
easy=math
题目大意：
输入一串数字, int类型, 输出这串数字的反转形式。注意反转的时候不能溢出了，因为范围是[$-2^{31},2^{31}-1$]。

个人思路：
先讲输入的int数字转换成string字符串,再用string的一些方便的操作进行反转，最后一步进行溢出判断。这题很简单，但是属于math范围下，我这个方法不是要求的那种。

代码：

class Solution:
    def reverse(self, x):
        """
        :type x: int
        :rtype: int
        """
        s = str(abs(x))
       
        if x >= 0:
            a = int(s[::-1]) #[开始位置，截位置，步长]
        else:
            a = -int(s[::-1])
        if (a > 2 ** 31 -1) or (a < -2 ** 31):
            return 0
        else:
            return a

遇到问题：
转换string不熟练：下面是一些总结

int(x [,base ])         将x转换为一个整数    
long(x [,base ])        将x转换为一个长整数    
float(x )               将x转换到一个浮点数    
complex(real [,imag ])  创建一个复数    
str(x )                 将对象 x 转换为字符串    
repr(x )                将对象 x 转换为表达式字符串    
eval(str )              用来计算在字符串中的有效Python表达式,并返回一个对象    
tuple(s )               将序列 s 转换为一个元组    
list(s )                将序列 s 转换为一个列表    
chr(x )                 将一个整数转换为一个字符    
unichr(x )              将一个整数转换为Unicode字符    
ord(x )                 将一个字符转换为它的整数值    
hex(x )                 将一个整数转换为一个十六进制字符串    
oct(x )                 将一个整数转换为一个八进制字符串 

Leetcode Q9 Palindrome Number
Math-easy

题目大意：
判断一个给定的数字是否是回文数，负数不是回文数，且不能用string的方式去解。
个人思路：
个人对于数学方面比较不敏感，这道题一上来只想着去用string去解，想不到用什么数学方法。看了别人的解。eg. 1221 将1221除以1000取整得到1，再将1221除以10取余得到1，就可以得到首位和末尾的值，在进行比较。这我确实是想不到的。

        a = 1
        if x < 0:
            return False
        #负数直接pass
        while((x/a) >= 10):
            a = a * 10
        #算出来第一位需要除多少
        while(a>10):
            last = x % 10
            init = x / a
            if (init != last):
                return False
            x = (x % a) / 10 #把首尾去掉
            a = a/100 #因为一行数字总共删去了首尾两个数字
        return True

问题：
1.经常对于循环，思路很不清晰不会写。比如这题第一个while循环，是为了找出除以多少可以找到首位。
2.一个比较傻的问题，while, if后直接加上一个变量x,意思是x为空false，不为空true。第二个循环是判断首尾是否相等。
我一开始进入了一个惯性思维，先/a取首位再%b取尾，然后比较是否相等。相等的话，a/10取前两位,b*10取后两位，进行比较，进行循环，直到a==b，结束这个循环。但其实是不对的，因为前两位和后两位，肯定不会是相等的，因为是reverse的。
这个小问题，卡了很久的时间，之后再做数字问题，要一步步试一下。

Leetcode Q20 Valid Parentheses
easy-stack,string

个人思路：
1.自己的想法，是分很多种情况，比如[]返回false, string里面为奇数的时候返回false。剩下的遍历去找，但是发现也会有([)]的情况。想的太表面了。
2.还是看了别人的代码。发现还是没有找到规律，一个正确的括号方式，把左右两半分开来，除了数量一定是一样的，顺序一定也是一一对应的。

eg.( [ { ( ) } ] ) { } 可以分为( [ { ( { 和) } ] ) }，无论有多复杂，只要是正确的括号方式，一定是一一对应的。

这也很符合堆栈的思想，最后进来先出去，一旦左右括号开始相接的那个地方，就开始一个个推回去。

class Solution:
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        stack = []
        dict = {'}':'{', ')':'(', ']':'['}
        # 对输入的string做一个遍历
        for char in s:
            # 判断如果char左括号的话，放在stack里
            if char in dict.values(): 
                stack.append(char)
            # 如果char是属于右括号，判断它作为key在dict里面的value是否和stack最后一个相等
            elif char in dict.keys():
                if stack == [] or dict[char] != stack.pop
                return False
            else
                return False
            return stack == []
            

dict用法：
字典是另一种可变容器模型，且可存储任意类型对象。
字典的每一个值key=>value，用冒号:分割，每个键值之间用逗号,隔开，整个字典包含在{}内。
d = {key1: value1, key2: value2} 是一种映射关系

# 用iteritems来遍历字典，返回的是一个迭代器？
d = dict(a=1, b=2, c=3)
for k, v in d.iteritems():
# 用items方法来遍历字典，返回一个列表，但是是无序的。
d = dict(a=1, b=2, c=3)
for k, v in d.items():
#使用get,pop来获取/删除key
get(key[, default])
#如果key在字典中，返回对应的value,否则返回default
pop(key[, default])
#如果key不在字典中，删除key回返回default

Q21 Merge Two Sorted Lists
easy- Linked List

个人思路：
链表上周才看过，但是遇到题目，知道步骤是什么，完全不知道怎么下手。也不知道原来要自己构建一个链表类，再去用。现在觉得数据结构可能需要换一本python的来看了，这样可以更加深理解。
copy了别人的代码，新建一个list，pre。遍历两个list，哪个小，就把指针指向哪一个。最后谁的列表先遍历光了，剩下的全部贴到pre里面。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeTwoLists(self, l1, l2):
        """
        :type l1: ListNode
        :type l2: ListNode
        :rtype: ListNode
        """
        pre = dummy = ListNode(None)
        while l1 and l2:
            if l1.val < l2.val:
                pre.next = l1
                l1 = l1.next
            else:
                pre.next = l2
                l2 = l2.next
            pre = pre.next
        pre.next = l1 or l2
        return dummy.next

数学part

第七章 参数估计

这章理解上有点难度

7.1 参数估计的基本原理

7.1.1 估计量与估计值

对于能够掌握全体的数据，只需要做一些简单的统计描述，就可以得到所关心的总体特征。eg. 总体均值，方差，比例等。但现实情况很复杂，有些现象的范围也比较广，不可能对总体中每个单位进行测量，这就需要从总体中稠一些个体进行调查，进而推断总体特征。

参数估计parameter estimation

就是用样本统计量去估计总体的参数。在参数估计中，用来估计总体参数的统计量称为估计量(estimator)，用符号$\hat{\theta }$表示。样本均值，样本比例，样本方差等都可以是一个估计量。如果将总体参数笼统地用一个符号$\theta$来表示，参数估计就是如何用$\hat{\theta }$来估计$\theta$的。

根据一个具体的样本计算出的估计量的数值称为估计值(estimated value)。

7.1.2 点估计与区间估计

1. 点估计(point estimate)：
   就是用样本统计量$\hat{\theta }$的某个取值直接作为总体参数$\theta$的估计值。比如用$\bar{x}$直接作为总体均值$\mu$的估计值等。虽然在重复抽样下，点估计均值数学期望等于总体真值，但样本是随机的，随机抽出一个具体的样本得到的估计值很可能不同于总体真值。

2. 区间估计(interval estimate)：
   所以，一个具体的点估计值无法给出估计的可靠性的度量，因此就不能完全依赖于一个估计值，而是围绕点估计值构造总体参数的一个区间，这就是区间估计。范围越大，真值在里面可能性更大。

区间估计是在点击出的基础上，给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。与点估计不同，进行区间估计时，根据样本统计量的抽样分布可以对样本统计量与总体参数的接近程度给一个概率度量。

以总体均值为例：再重复抽样或则无限总体抽样下，样本均值的学期望等于总体均值，$E(\bar{x})=\mu$，样本均值的标准误差为${\sigma }_{\bar{x}}=\frac{\sigma }{\sqrt{n}}$，由此克制样本均值$\bar{x}$落在总体均值$\mu$的两侧各为1个抽样标准差范围内的概率为0.682；落在2个抽样标准差范围概率为0.9545;落在3个抽样标准范围内概率为0.9973等。

实际上，相对着也是一样的。$\bar{x}$和$\mu$是对称的。通俗地说，如果抽取100个样本来估计总体均值，由100个样本所构造100个区间中，约有95个区间包含总体均值，另外5个不包含。

在区间估计中，由样本统计量所构造的总体参数的估计区间称为置信区间(confidence interval)，其中区间的最小值为之心下限，最大值称为置信上限。
比如抽取100个样本，每一个样本构造了一个置信区间，这样，由100个样本构造的总体参数的100个置信区间中，有95%的区间包含了总体参数的真值，5%则没有包含。95%这个值称为置信水平，也称为置信度或置信系数。

7.1.3 评价估计量的标准

参数估计是用样本量$\hat{\theta }$作为总体参数$\theta$的估计。实际上，用于估计$\theta$的估计量很多，也能根本均值，中位数等。究竟用哪种才是一个好的估计量呢？以下是一些标准

1. 无偏性
   无偏性(unbiasedness)指估计量抽样分布的数学期望等于被估计的总体参数。设总体参数为$\theta$，如果$E(\hat{\theta })=\theta$，则称$\hat{\theta }$为$\theta$的无偏估计量。
   
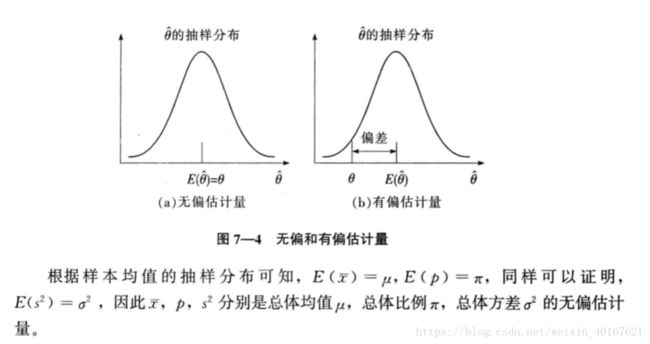
2. 有效性
   一个无偏的估计量并不意味着非常接近被估计的参数，它必须还比总体参数的离散程度小。有效性(efficiency)指对同一总体参数的两个无偏估计量，有更小标准差的估计量更有效。
   

7.2 一个总体参数的区间估计

如何用样本统计量来构造一个总体参数的置信区间

7.2.1 总体均值的区间估计

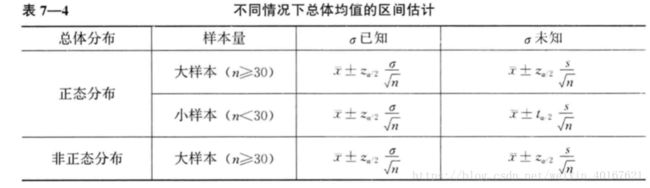
在总体均值进行区间估计时，需要考虑总体是否为正态分布，总体方差是否已知，用于构造估计量的样本是大样本(n>=30)还是小样本(n<=30)等几种情况。
1. 正态总体、方差已知，或非正态总体、大样本
当总体服从正态分布且${\sigma }^2$已知时，或者总体不是正态分布但是大样本时，样本均值$\hat{x}$的抽样分布均为正态分布，其数学期望为总体准均值$\mu$，方差为$\frac{{\sigma }^2}{n}$，而样本均值经过标准化后的随机变量则服从标准正态分布。

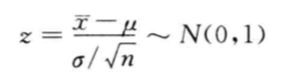可得出总体均值$\mu$在$1-a$置信水平下的置信区间为：

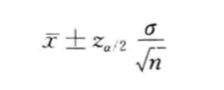
a是实现所确定的一个概率值，也称为风险值，它是总体不包括在置信区间的概率；1-a称为置信水平。也就是说，总体均值由点估计值和描述估计量精度的值组成。

如果总体服从正态分布但是${\sigma }^2$位置，或总体并不服从正态分布，只要是在大样本条件下，总体方差可以用样本方差代替。

2. 正态总体、方差未知、小样本
只要总体服从弄正态分布，无论样本量如何，样本均值$\hat{x}$的抽样分布都服从正态分布。这时，样本均值经过标准化以后的随机变量则服从自由度为(n-1)的t分布,即

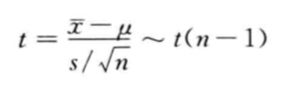
因此需要采用t分布来建立总体均值$\mu$的置信区间。

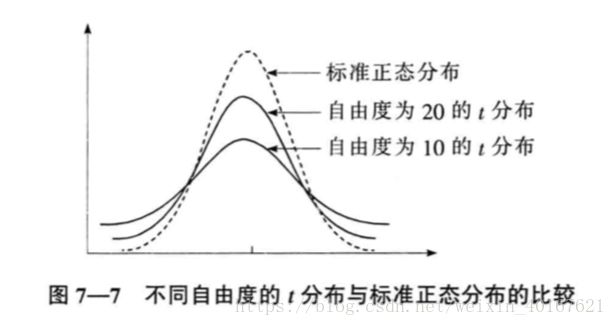
根据t分布建立的总体均值$\mu$在1-a的置信水平下的置信区间为：

总结：

7.2.2 总体比例的区间估计

大样本情况下，由样本比例p的抽样分布可知，样本量够大时，比例p的抽样分布可用正态分布近似。p的数学期望为$E(p)=\pi$；$p$的方差为${\sigma }_p^2=\frac{\pi (1-\pi )}{n}$。

这时，总体比例的置信区间为：
$p\pm z_{a/2}\sqrt{\frac{p(1-p)}{n}}$
式中，a是显著性水平；$z_{a/2}$是标准正态分布$a/2$时的$z$值。

7.2.3 总体方差的区间估计

只讨论正态总体的方差估计问题。根据样本方差的抽样分布可知，样本方差服从自由度为$n-1$的${\chi }^2$分布。因此用${\chi }^2$分布来构造总体方差的置信区间。
可推导，总体方差${\sigma }^2$在$1-a$置信水平下的置信区间为:

下图总结了一个总体参数估计的不同情形以及所使用的分布

7.3 两个总体参数的区间估计

对于两个总体，我们一般关心的是两个总体的均值之差${\mu }_1-{\mu }_2$，两个总体的比例之差${\pi }_1-{\pi }_2$，两个总体的方差比为${\sigma }_1^2/{\sigma }_2^2$等。

7.3.1 两个总体均值之差的区间估计

设俩总体的均值分别为${\mu }_1$和${\mu }_2$，从两个总体中分别抽取样本量为$n_1$和$n_2$的两个随机样本，其样本均值为$\overline{x_1}$和$\overline{x_2}$。两个总体均值之差${\mu }_1-{\mu }_2$的估计量显然为两个样本的均值之差$\overline{x_1}-\overline{x_2}$。

1.两个总体均值之差的估计：独立样本

(1)大样本的估计
如果两个样本是从两个总体中独立抽取的，即一个样本中的元素与另一个样本中的元素相互独立，则称为独立样本。如果两个总体都为正态分布，或者两个总体不服从正态分布但两个样本都为大样本，两个样本均值之差$\overline{x_1}-\overline{x_2}$的抽样分布服从期望值为$({\mu }_1-{\mu }_2)$，方差为$(\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2})$的正态分布，则两个样本均值之差经标准化后则服从标准正态分布。
当两个总体的方差已知，两个总体均值之差在$1-a$置信水平下的置信区间为：

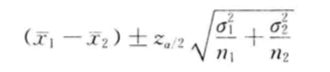当两个总体的方差未知时，可用两个样本方差来代替：

(2) 小样本估计
在两个都为小样本时，为估计两个总体的均值之差，要做出以下假定。
1)两个总体都服从正态分布
2)两个随机样本独立地分别抽自两个总体
在上述假定下，无论样本量的大小，两个样本均值之差都服从正态分布。当两个总体方差已知时，可用大样本1式建立置信区间。若两个方差未知，有以下几种情况：
1)总体方差未知但相等，即${\sigma }_1^2={\sigma }_2^2$，需要用两个样本的方差$s_1^2$和$s_2^2$来估计，这是需要将两个样本的数据组合在一起，以给出总体方差的合并估计量$s_p^2$：

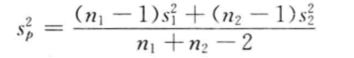
这时，两个样本均值之差置信区间为：

2)当两个总体方差未知且不想等，两个样本均值之差经标准化后金丝服从自由度为$v$的$t$分布，自由度$v$的计算公式为：

两个总体均值之差在$1-a$置信水平下的置信区间为：

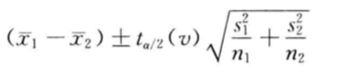
2.两个总体均值之差的估计：匹配样本
是用上述方法，会有弊端。

eg. 为估计两种方法组装产品所需要时间的差异，分别对两种不同的组装放大各随机安排12工人。

会有一些几率，会将一波很差的工人安排到a方法上，另一波都很好的工人安排到b方法上。
所以，为了避免这种问题，可以使用匹配样本(matched sample)，即一个样本重的数据与另外样本的数据相对应，比如用同一拨工人用两种方法。

使用匹配样本进行估计时，大样本条件下，两个总体均值之差${\mu }_d={\mu }_1-{\mu }_2$在$1-a$置信水平下的置信区间为:

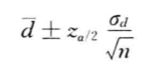
$d$表示两个匹配样本对于数据的差值;$\bar{d}$表示各差值的均值；${\sigma }_d$表示个差值的标准差。总体差值的标准差未知时，可用样本差值的标准差代替。

7.3.2 两个总体比例之差的区间估计

eg. 收视率的应用

从两个二项总体中抽出两个独立的样本，则两个样本比例之差的抽样分布服从正态分布。同样，俩样本的比例之差经标准化后则服从标准正态分布：

因此，根据正态分布建立的两个总体比例之差${\pi }_1-{\pi }_2$在$1-a$置信水平下的置信区间为：

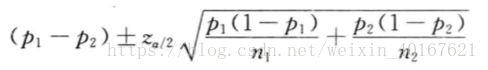
7.3.3 两个总体方差比的区间估计

eg. 比较用两种不同方法生产的产品性能的稳定性；不同测量工具的精度
具体略

两个总体参数估计的不同情形及所使用的分布

7.4 样本量的确定

在进行估计之前，总希望提高估计的可靠程度，但在一定的样本量之下，要提高估计程度，就要扩大置信区间。但一昧的扩大是没有意义的，比如确信一年之中肯定下雨这件事。所以想要缩小置信区间，有不降低置信程度，就需要增加样本量。

7.4.1 估计总体均值时样本量的确定

总体均值的置信区间是由样本均值$\bar{x}$和估计误差两部分组成的。令$E$代表所希望达到的估计误差，即
$E=z_{\alpha /2}\frac{\sigma }{\sqrt{n}}$
由此可以推导出确定样本量的公式如下：

$n=\frac{(z_{\alpha /2}{)}^2{\sigma }^2}{E^2}$
式中e值是使用者在置信水平下可以接受的误差。

7.4.2 估计总体比例时样本量的确定

与估计总体均值时样本量的确定方法类似，$z_{\alpha /2}$的值，总体比例$\pi$和样本量$n$确定了估计误差的大小。
推导过程省略，确定样本量公式如下：