字符串算法:正则表达式原理及C++实现
前言
原理
1.链接操作:即所指示的东西同时出现,如"AB"即代表我们检索的文本中必须出现"AB"才行;
2.或操作:即所指示的东西,至少有一个出现,我们用符号"|"来代表或操作,如"A|B"即代表我们检索的文本中必须出现"A"或者"B"或者都出现;
3.闭包操作:闭包操作即将模式的部分重复任意的次数,我们用"*"来表示闭包操作,如"A*"表示检索文本中有0个到无穷个"A"都会检索成功;
4.括号操作:括号用来表示模式的优先级,我们使用"()"来表示,如"(AC)|B"表示检索文本中有无"AC"或"B";
说了这么多,你也可能没怎么看懂,我举几个例子吧:
表达式:(A|B)(C|D) ;匹配字符串:AC、AD、BC、BD
表达式:A(B|C)*D ;匹配字符串:AD、ABD、ACD、ABCD、ABBD、ACCD、ABCCBD.......
表达式:A*|(A*BA*BA*)* ;匹配字符串:AAA、BBAABB、BABAAA.......
非确定有限状态自动机(NFA)
在这里,我们要提出一个概念及非确定有限状态自动机(NFA),与之前博客中提到的确定有限状态自动机(DFA)类似,NFA也是一种状态机,且因为我们给出确定的模式,其状态数也是确定,但是因为我们支持或操作以及闭包操作,因此其状态是不确定的,所以其方法与KMP算法中还有所不同。在NFA中,我们将根据不同的操作,构建我们的状态机:
1.链接操作:链接操作会是整个NFA构建中最简单的部分,我们只需将其与下一个状态进行转换即可,但是我们不能在状态机中对他们进行连接;
2.括号操作:因为括号操作涉及到了优先级问题,因此我们先将其与下一个状态进行链接,之后使用栈来处理它,当遇到左括号压栈,遇到右括号弹栈,并构建一条右括号到下一个状态的路径;
3.闭包操作:因为闭包操作需要进行任意次数的重复,因此我们将允许在状态机中对其进行来回往复,多次到达同一个状态,即将"*"状态与其对应的字符进行双向链接,若闭包操作对象有括号操作,那么我们应该对左括号进行双向链接,最后我们将"*"状态与下一状态进行连接;
4.或操作:或操作将是NFA构建中最难的一部分,我们将根据是否有括号,将其分为两种你处理,当没有括号时,我们将从"|"状态出进行分叉,将其链接到模式末尾,同时将起始状态链接到"|"状态的下一状态;当有括号时,我们将其链接到下一个右括号处,将左括号链接到"|"状态的下一状态;
以上即为我们所有的NFA构建操作,值得我们注意的是,我们并不会将相邻的状态之间构建通路,只有我们在处理括号、闭包以及或运算时才会产生新的路径,这是帮助理解NFA构建的至关重要的一步。
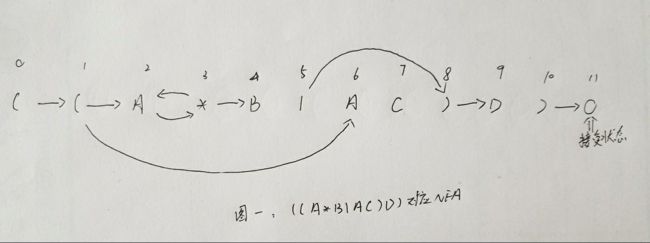
这里将给出一个例子帮助大家理解:
我们构建"((A*B|AC)D)"的NFA将会如下所示:
代码如下所示:
/* NFA构建函数:根据正则表达式构建对应的NFA
* 参数:regexp:用于构建NFA的正则表达式
* 返回值:无
*/
void RegularExp::NFA(string regexp) {
stack ops;
// 储存正则表达式并获取其长度
re = regexp;
M = regexp.length();
// 构建新的有向图
G = new Graph(M + 1);
// 遍历整个正则表达式
for (int i = 0; i < M; i++) {
int lp = i; // 储存起始位置
// 碰到'('或'|'则将该位置压入栈中,即进行括号配对
if (re[i] == '(' || re[i] == '|')
ops.push(i);
// 括号配对
else if (re[i] == ')') {
int or = ops.top();
ops.pop();
// 处理括号中有'|'的特殊情况
// --------------------------------------有待改进------------------------------------------------------------
if (re[or] == '|') {
lp = ops.top();
ops.pop();
// 链接或符号
G->addEdge(lp, or +1);
G->addEdge(or , i);
}
//-----------------------------------------------------------------------------------------------------------
else
lp = or ;
}
// 当其下一位为闭包操作时
if (i < M - 1 && re[i + 1] == '*') {
// 进行双向链接
G->addEdge(lp, i + 1);
G->addEdge(i + 1, lp);
}
// 特定符号直接连向下一位
if (re[i] == '(' || re[i] == '*' || re[i] == ')')
G->addEdge(i, i + 1);
}
} 模式扫描
当我们构建好了NFA后,我们即可根据构建好的NFA进行模式扫描,但在开始之前我们需要了解到,NFA是不确定状态自动机,意味着我们当前可能处于多个不同的状态,这是有可能的,但是我们的最终目的是到达接受状态,那意味着我们完成正则表达式的识别。因此,我们在扫描的过程中,将会用到一些数据结构来暂时储存当前所有可能的状态,并在读取下一个字符的字符的时候,根据读取的字符更新状态。当然,我们还有一些特别的规则,那就是我们可以到达所有链接的路径,因为在构建NFA的时候,我们并没有将链接操作构建通路,只是将可以略过或者重复的括号操作、闭包操作以及或操作进行了路径构建,因此这将是一个路径的可达性问题;而对于链接操作,我们将会在识别下一个字符时自动进行跳转。
这是一个非常抽象的过程,建议大家可以看看《算法——第四版》中的字符串章节,将会有更清晰的认识。
代码如下:
/* 识别函数:根据以及构造好的NFA识别目标文本
* 参数:txt:用于识别的目标文本
* 返回值:bool:若目标文本匹配正则表达式返回tru,否则返回false
*/
bool RegularExp::Recognize(string txt) {
// 构造Bag
Bag pc;
// 构造DFS搜索器
DirectedDFS *dfs = new DirectedDFS();
// 根据有向图G初始化DFS搜索器
dfs->Init(*G);
// 从第一个顶点开始进行DFS搜索
dfs->DFS(*G, 0);
// 依次将从第一个顶点可达顶点加入Bag
for (int v = 0; v < G->V(); v++)
if (dfs->Marked(v))
pc.Insert(v);
// 遍历整个文本
for (int i = 0; i < txt.length(); i++) {
// 构建匹配Bag
Bag match;
// 遍历所有可达顶点
for (int v = 0; v < pc.Length(); v++)
if (pc[v] < M)
if (re[pc[v]] == txt[i] || re[pc[v]] == '.') // 获取所有可能的匹配并加入match
match.Insert(pc[v] + 1);
// 重置Bag以及DFS搜索器
pc.MakeEmpty();
dfs->MakeEmpty();
// 通过有向图G初始化DFS搜索器
dfs->Init(*G);
// 将所有匹配文本对应位置的节点进行DFS搜索
for (int i = 0; i < match.Length(); i++)
dfs->DFS(*G, match[i]);
// 依次将所有可达节点加入Bag
for (int v = 0; v < G->V(); v++)
if (dfs->Marked(v))
pc.Insert(v);
}
// 遍历所有可达节点
for (int i = 0; i < pc.Length(); i++)
if (pc[i] == M) // 判断是否匹配正则表达式
return true;
return false;
}
上述代码中,有几个结构是自己写的:Graph,DirectedDFS,Bag三个类,分别为图类,深度优先搜索器以及包类(应该可以用Set替代),我将会给出他们的.h文件,以及完整的正则表达式文件各位可以按自己的喜好来写。
C++实现
#include
using namespace std;
// 重命名边节点,便于操作
typedef struct ArcNode *Position;
/* 边节点
* 储存元素:
* ArcName:该边指向的节点
* Next:以该边的头结点为头结点的其他边
*/
struct ArcNode {
int ArcName;
Position Next;
};
/* 顶点节点
* 储存元素:
* Name:该顶点的名字
* FirstArc:以该顶点为头结点的第一个边
*/
struct VexNode {
int Name;
Position FirstArc;
};
/* Graph类:有向图类
* 接口:
* MakeEmpty:置空整个有向图,不重置顶点只重置边
* addEdge:向有向图中添加新的有向边
* V:获取图中的顶点个数
*/
class Graph
{
public:
// 构造函数
Graph(int);
// 析构函数
~Graph();
// 友元类
friend class DirectedDFS;
// 接口函数
void MakeEmpty();
void addEdge(int from, int to);
int V();
private:
// 数据成员
int VexNum; // 顶点个数
int ArcNum; // 边个数
VexNode *AdjList; // 邻接表
};
#endif
DirectedDFS.h:
#ifndef DIRECTEDDFS_H
#define DIRECTEDDFS_H
#include
#include "Graph.h"
using namespace std;
/* DirectedDFS类:对指定的Graph进行DFS搜索
* 接口:
* MakeEmpty:重置DFS搜索器
* Init:使用指定的Graph来初始化搜索器
* DFS:对初始化后的DFS搜索器根据指定Graph以及指定节点进行DFS搜索
* Marked:返回搜索结果
*/
class DirectedDFS
{
public:
// 构造函数
DirectedDFS();
// 析构函数
~DirectedDFS();
// 接口函数
void MakeEmpty();
void Init(const Graph &);
void DFS(const Graph &, int);
bool Marked(int);
private:
// 数据成员
bool *Table; // 储存DFS搜索结果
};
#endif Bag.h:
#ifndef BAG_H
#define BAG_H
#include
using namespace std;
/* Bag类:储存元素只允许存入元素,不允许删除
* 接口:
* MakeEmpty:重置功能,重置整个Bag
* Length:返回Bag的大小,即储存元素个数
* Insert:向Bag中插入元素
* 重载:
* []:下标运算符,返回Bag中第i个元素
*/
class Bag
{
public:
// 构造函数
Bag();
// 析构函数
~Bag();
// 重载运算符
int& operator [](int);
// 接口函数
void MakeEmpty();
int Length();
void Insert(int);
private:
// 数据成员
int *Elems; // 储存元素
int Size; // Bag中元素个数
int MaxSize; // Bag当前可储存元素个数
};
#endif
最后给出的将是整个ReularExpression的代码:
#ifndef REGULAREXP_H
#define REGULAREXP_H
#include
#include
#include
#include "Bag.h"
#include "Graph.h"
#include "DirectedDFS.h"
using namespace std;
/* RegularExp类:正则表达式检索器
* 接口:
* MakeEmpty:重置整个正则表达式检索器
* NFA:根据正则表达式构造NFA(非确定有限状态自动机)
* Recognize:判断目标文本是否匹配正则表达式
*/
class RegularExp
{
public:
// 构造函数
RegularExp();
// 析构函数
~RegularExp();
// 接口函数
void MakeEmpty();
void NFA(string);
bool Recognize(string);
private:
// 数据成员
int M; // 储存正则表达式字符个数
string re; // 储存正则表达式
Graph *G; // 储存NFA构建的有向图
};
#endif // !REGULAREXP_H
#include "RegularExp.h"
/* 构造函数:初始化对象
* 参数:无
* 返回值:无
*/
RegularExp::RegularExp() {
G = NULL;
}
/* 析构函数:对象消亡时回收储存空间
* 参数:无
* 返回值:无
*/
RegularExp::~RegularExp() {
MakeEmpty();
}
/* 重置函数:重置正则表达式检索器
* 参数:无
* 返回值:无
*/
void RegularExp::MakeEmpty() {
// 删除旧的NFA有向图
delete G;
G = NULL;
}
/* NFA构建函数:根据正则表达式构建对应的NFA
* 参数:regexp:用于构建NFA的正则表达式
* 返回值:无
*/
void RegularExp::NFA(string regexp) {
stack ops;
// 储存正则表达式并获取其长度
re = regexp;
M = regexp.length();
// 构建新的有向图
G = new Graph(M + 1);
// 遍历整个正则表达式
for (int i = 0; i < M; i++) {
int lp = i; // 储存起始位置
// 碰到'('或'|'则将该位置压入栈中,即进行括号配对
if (re[i] == '(' || re[i] == '|')
ops.push(i);
// 括号配对
else if (re[i] == ')') {
int or = ops.top();
ops.pop();
// 处理括号中有'|'的特殊情况
// --------------------------------------有待改进------------------------------------------------------------
if (re[or] == '|') {
lp = ops.top();
ops.pop();
// 链接或符号
G->addEdge(lp, or +1);
G->addEdge(or , i);
}
//-----------------------------------------------------------------------------------------------------------
else
lp = or ;
}
// 当其下一位为闭包操作时
if (i < M - 1 && re[i + 1] == '*') {
// 进行双向链接
G->addEdge(lp, i + 1);
G->addEdge(i + 1, lp);
}
// 特定符号直接连向下一位
if (re[i] == '(' || re[i] == '*' || re[i] == ')')
G->addEdge(i, i + 1);
}
}
/* 识别函数:根据以及构造好的NFA识别目标文本
* 参数:txt:用于识别的目标文本
* 返回值:bool:若目标文本匹配正则表达式返回tru,否则返回false
*/
bool RegularExp::Recognize(string txt) {
// 构造Bag
Bag pc;
// 构造DFS搜索器
DirectedDFS *dfs = new DirectedDFS();
// 根据有向图G初始化DFS搜索器
dfs->Init(*G);
// 从第一个顶点开始进行DFS搜索
dfs->DFS(*G, 0);
// 依次将从第一个顶点可达顶点加入Bag
for (int v = 0; v < G->V(); v++)
if (dfs->Marked(v))
pc.Insert(v);
// 遍历整个文本
for (int i = 0; i < txt.length(); i++) {
// 构建匹配Bag
Bag match;
// 遍历所有可达顶点
for (int v = 0; v < pc.Length(); v++)
if (pc[v] < M)
if (re[pc[v]] == txt[i] || re[pc[v]] == '.') // 获取所有可能的匹配并加入match
match.Insert(pc[v] + 1);
// 重置Bag以及DFS搜索器
pc.MakeEmpty();
dfs->MakeEmpty();
// 通过有向图G初始化DFS搜索器
dfs->Init(*G);
// 将所有匹配文本对应位置的节点进行DFS搜索
for (int i = 0; i < match.Length(); i++)
dfs->DFS(*G, match[i]);
// 依次将所有可达节点加入Bag
for (int v = 0; v < G->V(); v++)
if (dfs->Marked(v))
pc.Insert(v);
}
// 遍历所有可达节点
for (int i = 0; i < pc.Length(); i++)
if (pc[i] == M) // 判断是否匹配正则表达式
return true;
return false;
} 那么整个正则表达式到这里就完了,其中我也有很多没弄好的地方,以后会不断的更在,大家如果有什么意见也请提出来,大家共同进步就好啦~~
参考文献:《算法——第四版》,百度百科