LeetCode简单题

1：一 两数之和

问题描述：

给定一个整数数组和一个目标值，找出数组中和为目标值的两个数。

你可以假设每个输入只对应一种答案，且同样的元素不能被重复利用。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

问题分析：

可以通过普通的爆破法，写两个for循环进行求解。这样最简单，但是时间复杂度有O(n^2),空间复杂度O(1).
也可以通过一遍哈希表法。在进行迭代并将元素插入到表中的同时，我们还会回过头来检查表中是否
已经存在当前元素所对应的目标元素。如果它存在，那我们已经找到了对应解，并立即将其返回。这样
的时间复杂度是O(n)，空间复杂度也是O(n)
也就是说，我们会弄一个对应关系（哈希），在对应关系里找很快的（O(1)），用空间换取时间。
再加上for循环耗去的O(n)的时间，总共的复杂度是O(n)。

问题解决方案1：

#####双重for循环爆破，耗时7272ms，对于python程序员来说这个是致命的。python本来就慢。
class Solution:
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        for i in range(len(nums)):
            for j in range(i+1,len(nums)):
                if nums[i]+nums[j] == target:
                    return [i,j]

s = Solution()
nums = [1,2,3,4,5,6]
target = 10
l = s.twoSum(nums,target)
print(l)

问题解决方案2：

#######应用了python的dict来实现一遍哈希表，大大降低了时间复杂度（为之前的1/151）。为48ms。
class Solution:
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        d = {}#按照键值对的方式存储数据 下标为值，真正的值为键
        for i in range(len(nums)):
            if target - nums[i] in d.keys():
                return [d[target-nums[i]],i]
            d[nums[i]] = i

s = Solution()
nums = [1,2,3,4,5,6]
target = 10
l = s.twoSum(nums,target)
print(l)

Java版AC代码：

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i = 0; i < nums.length; ++i){
            if(!map.containsKey(target - nums[i])){
                map.put(nums[i],i);
            }
            else{
                int res[] = {map.get(target - nums[i]),i};
                return res;
            }
        }
        return null;
    }
}

7：七 反转整数

问题描述：

给定一个 32 位有符号整数，将整数中的数字进行反转。

示例 1:

输入: 123
输出: 321


 示例 2:

输入: -123
输出: -321


示例 3:

输入: 120
输出: 21


注意:

假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−231,  231 − 1]。根据这个假设，如果反转后
的整数溢出，则返回 0。

问题分析：

正常用C等语言写，需要用到数组，特别的麻烦。但是Python不用这么玩。
python可以将数字转换成字符串，然后将字符串进行反转，遍历字符串的每一位，分别是a*10+(a+1)就
可以了。

问题解决方案：

class Solution:
    def reverse(self, x):
        """
        :type x: int
        :rtype: int
        """
        t = x#将x暂存，确定要返回的是正数还是负数
        t = abs(t)
        st = str(t)
        lt = list(st)
        lt = lt[::-1]
        sum = 0
        for i in lt:
            sum = sum*10 + int(i)
        if abs(sum)

result:

-125

9:九 回文数

问题描述：

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例 1:

输入: 121
输出: true


示例 2:

输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。


示例 3:

输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。


进阶:

你能不将整数转为字符串来解决这个问题吗？

问题分析：

普通的用python来写的话会非常的容易。直接将数字转成字符串，判断反转后的字符串是否等于
原字符串即可。
进阶：说了不能转成字符串，我们会想到反转数字。通过%10和/10来操作。
经过仔细思考，我们发现这样有可能会面临溢出问题，这时就需要加以判断，增加题目难度。
其实，只反转一半的数字就可以。把后半段数字反转成一个num.如果num和x是10倍关系，或者相等，就
是回文数，我们不care位数是奇数还是偶数，因为如果是奇数我们可以通过10倍关系来判断。
比如52225  我们通过反转后半边数字，得到52  左半边经过操作之后是520 是10倍关系，也可以左半边
反转后是522 左边是52，反转后除以10是52（整除），依然相等。这两种办法取决于你怎么写你的
循环退出条件。

问题解决方案1：

class Solution:
    def isPalindrome(self, x):
        """
        :type x: int
        :rtype: bool
        """
        s = str(x)
        s1 = s[::-1]
        if s == s1:
            return True
        else:
            return False
s = Solution()
res = s.isPalindrome(1001)
print(res)

问题解决方案2：

class Solution:
    def isPalindrome(self, x):
        """
        :type x: int
        :rtype: bool
        """
        if x < 0 or (x%10 == 0 and x!=0):
            return False
        num = 0
        while x > num:
            num = num*10 + x%10
            x//=10
        if x == num or x == num//10:
            return True
        else:
            return False
s = Solution()
res = s.isPalindrome(1001)
print(res)

13：十三 罗马数字转整数

问题描述：

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做  XXVII, 即
为XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字
 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个
 特殊的规则只适用于以下六种情况：


	I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
	X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。 
	C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。


给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

示例 1:

输入: "III"
输出: 3

示例 2:

输入: "IV"
输出: 4

示例 3:

输入: "IX"
输出: 9

示例 4:

输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.


示例 5:

输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

问题分析：

乍一看一头雾水，仔细看看还是能发现规律的。
其实这就是一个不等长多关键字的字符串的匹配问题。
我把需要匹配的子串放到了一个字典里
d = {'I':1,'V':5,'X':10,'L':50,'C':100,'D':500,'M':1000,
     'IV':4,'IX':9,'XL':40,'XC':90,'CD':400,'CM':900}
 然后就是匹配问题了。
 由于是匹配不定长的模式串，所以针对这个问题，应该一次性读取2个字符，
 如果这两个字符匹配上了，就把他们从队列中删除，如果没匹配上，就把第一个字符进行匹配（这个
 是一定可以匹配上的），然后把它从队列中删除，这样可以保证不会匹配出错。

问题解决方案：

class Solution:
    def romanToInt(self, s):
        """
        :type s: str
        :rtype: int
        """
        d = {'I':1,'V':5,'X':10,'L':50,'C':100,'D':500,'M':1000,
             'IV':4,'IX':9,'XL':40,'XC':90,'CD':400,'CM':900}
        sums = 0
        while len(s)>1:
            ab = s[:2]
            if ab in d.keys():
                sums += d[ab]
                s = s[2:]
            else:
                sums += d[s[0]]
                s = s[1:]
        if len(s):
            sums += d[s[0]]
        else:
            return sums
        return sums

s = Solution()
print(s.romanToInt('LVIII'))

14：十四：最长公共前缀

问题描述：

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]
输出: "fl"


示例 2:

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。


说明:

所有输入只包含小写字母 a-z 。

问题分析：

最长公共子串，注意是公共，所以说这决定了最长不过是字符串列表中最短的那个字符串的长度。
我们可以获取到这个最短的字符串的长度值min_lenth。判断字符串列表中的所有字符串是不是都以
第一个串的开头min_lenth长度的子串(current_str)开头，如果不是，就说明这个min_lenth
不是真正的min_lenth,所以要减1之后继续循环。如果字符串列表中的所有串都是以current_str开头，就
可以返回current_str串了。

问题解决方案：

class Solution:
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        min_lenth = None
        for i in strs:
            if min_lenth == None:
                min_lenth = len(i)
            else:
                if min_lenth > len(i):
                    min_lenth = len(i)
        if min_lenth == 0:
            return ''
        current_str = ''
        while min_lenth:
            current_str = strs[0][:min_lenth]
            for i in strs:
                if not i.startswith(current_str):
                    break
            else:
                break
            min_lenth -= 1
            continue
        if min_lenth == 0:
            return ''
        else:
            return current_str

20 ： 二十 ： 有效的括号

题目描述：

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

各种示例：

输入: "()"
输出: true
输入: "()[]{}"
输出: true
输入: "(]"
输出: false
输入: "([)]"
输出: false
输入: "{[]}"
输出: true

题目分析：

根据分析发现，可以用栈来解决。
如果是空串，则返回True
如果不是空串，遇到左侧符号就入栈，遇到右侧符号先判断栈是否空，如果空返回False
如果不空的话，就判断栈顶元素和栈外元素是否配对，不配对直接返回False
处理完之后，如果栈是空的，返回True
如果栈非空，返回False

解决方案1 超过百分之99的人：

class Solution:
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        if s == '': # 空字符串直接返回True
            return True
        stack = []
        for i in s:
            if i == '{' or i == '(' or i == '[':
                stack.append(i)
            else:
                if not len(stack): # 右侧符号遇到栈空，直接返回False
                    return False
                if i == '}' and stack[-1] == '{':
                    stack.pop()
                elif i == ')' and stack[-1] == '(':
                    stack.pop()
                elif i == ']' and stack[-1] == '[':
                    stack.pop()
                else:
                    return False # 栈外没有与栈顶配对，返回False
        if len(stack): # 处理完之后栈非空，返回False
            return False
        return True

解决方案2：

class Solution:
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        if s == '': # 空字符串直接返回True
            return True
        stack = []
        mapping = {')':'(','}':'{',']':'['}
        for i in s:
            if i in mapping.values():
                stack.append(i)
            else:
                if not len(stack): # 右侧符号遇到栈空，直接返回False
                    return False
                elif mapping[i] == stack[-1]:
                    stack.pop()
                else:
                    return False # 栈外没有与栈顶配对，返回False
        if len(stack): # 处理完之后栈非空，返回False
            return False
        return True

21:二十一：合并两个有序链表

题目描述：

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

题目示例：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

题目分析：

可以只用现有的结点进行连接，这样可以避免新申请一个m+n的链表导致申请那么多的结点的时间耗费。
具体写了个逻辑，自认为效率很高，但是效果没有用递归好，因为我用了几个中间变量暂存。
估计时间是耗费在这儿了。先贴自己不是很成熟的代码。

解决方案1：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeTwoLists(self, l1, l2):
        """
        :type l1: ListNode
        :type l2: ListNode
        :rtype: ListNode
        """
        flag = True
        head = None
        current = None
        while l1 or l2:
            if flag:
                flag = False
                if not l1:
                    return l2
                if not l2:
                    return l1
                if l1.val < l2.val:
                    head = l1
                    current = head
                    l1 = l1.next
                else:
                    head = l2
                    current = head
                    l2 = l2.next
            else:
                if not l1:
                    current.next = l2
                    return head
                if not l2:
                    current.next = l1
                    return head
                if l1.val < l2.val:
                    current.next = l1
                    current = l1
                    l1 = l1.next
                else:
                    current.next = l2
                    current = l2
                    l2 = l2.next
        return head

然后膜拜了大神的递归写法。（其实我觉得可以称之为动规了）
解决方案2：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeTwoLists(self, l1, l2):
        """
        :type l1: ListNode
        :type l2: ListNode
        :rtype: ListNode
        """
        if not l1 or l2:
            return l1 or l2 # 还新get了这种写法
        if l1.val < l2.val:
            l1.next = self.mergeTwoLists(l1.next,l2)
            return l1
        else:
            l2.next = self.mergeTwoLists(l1,l2.next)
            return l2

get到的新写法：

正常应用xx and xxx或者 xx or xxx时，会返回一个布尔值。
但是这种做法有一个新的应用。
在python中， return xx and xxx 和  return  xx or xxx有新的用法。
and 和 or 是短路原则的。
对于and来讲，如果左侧表达式为假，则不执行右侧表达式。如果左侧表达式为真，则执行右侧表达式。
所以，对于return xx and xxx来讲，如果xx为假，则直接return xx. 如果xx为真，则不管xxx为真还是假，
都返回xxx.

对于or 来讲，如果左侧表达式为真，则直接return xx. 如果左侧表达式为假，则直接return xxx。
一定要注意，return xxx and xx  和 return xxx or xx 时，return 的不是一个布尔值，而是xx 或者xxx

26. 二十六：删除排序数组中的重复项

题目描述：

给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

题目示例：

给定数组 nums = [1,1,2], 

函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 

你不需要考虑数组中超出新长度后面的元素。

给定 nums = [0,0,1,1,1,2,2,3,3,4],

函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。

你不需要考虑数组中超出新长度后面的元素。

题目分析：

好久没码代码了。竟然一直纠结于数据结构中删除重复元素那种写法。
遍历中修改列表可是大忌。。 会错乱的。
因为要求空间复杂度为0，所以显然不能新申请一个列表来存不同的元素。
所以想到了元素覆盖。怎么做呢？设置一个cont作为'新'列表的下标，遇到重复的元素直接跳过，
如果不是重复的元素，就存到cont中，另外cont自增一下。
这样循环下去，不重复的元素会跑到数组的前端，然后数组后面的东西就不用管了。

实现代码：

class Solution:
    def removeDuplicates(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        cont = 0
        for i, v in enumerate(nums):
            if not i: # 初始化第一个元素
                cont += 1
                continue
            if v == nums[i - 1]: # 如果重复元素就跳过去
                continue
            else: # 如果不重复，就加入到'新'列表中
                nums[cont] = v
                cont += 1
        return cont

27：二十七：移除元素

题目描述：

给定一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

题目示例：

给定 nums = [3,2,2,3], val = 3,

函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。

你不需要考虑数组中超出新长度后面的元素。

给定 nums = [0,1,2,2,3,0,4,2], val = 2,

函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

注意这五个元素可为任意顺序。

你不需要考虑数组中超出新长度后面的元素。

解题思路：

和上个题差不多，但是思路稍微有点差别。因为上个题是有序数组去重，所以当前元素得和前一个元素
对比看看是否相同。所以开头第一个元素不用比较，直接加入'新'列表。
这个题目就不用区别是否第一个元素了，直接跟val比较，不同就加入'新'列表，相同就跳过。

解决方案：

class Solution:
    def removeElement(self, nums, val):
        """
        :type nums: List[int]
        :type val: int
        :rtype: int
        """
        cont = 0
        for i, v in enumerate(nums):
            if v == val: # 如果重复元素就跳过去
                continue
            else: # 如果不重复，就加入到'新'列表中
                nums[cont] = v
                cont += 1
        return cont

28 二十八：实现strStr()

题目描述：

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回  -1。

问题示例：

输入: haystack = "hello", needle = "ll"
输出: 2
输入: haystack = "aaaaa", needle = "bba"
输出: -1

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的
 indexOf() 定义相符。

解题思路：

如果是空串，返回0
如果不是空串，用in运算符看看needle是不是在haystack里，如果不在，返回-1
如果在，则看看haystack[i:i+lenth] 是否等于needle 。如果相等，则返回i

解决方案：

class Solution:
    def strStr(self, haystack, needle):
        """
        :type haystack: str
        :type needle: str
        :rtype: int
        """
        if not needle:
            return 0
        if needle not in haystack:
            return -1
        lenth = len(needle)
        for i,v in enumerate(haystack):
            if v == needle[0] and haystack[i:i+lenth] == needle:
                return i

35 三十五：搜索插入位置

题目描述：

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它
将会被按顺序插入的位置。

你可以假设数组中无重复元素。

题目示例：

输入: [1,3,5,6], 5
输出: 2
输入: [1,3,5,6], 2
输出: 1
输入: [1,3,5,6], 7
输出: 4
输入: [1,3,5,6], 0
输出: 0

解题思路：

想朴素的解决问题很简单，因为是有序的数组，寻找插入位置，只要列表中的元素大于等于target，就可以返回
这个下标了。当然啦，如果遍历完成都没找到大于等于target的元素，那么就返回这个列表的长度。

后来想了想，有序数组，为啥不用二分来找呢，这样不是更快么。只不过二分找的是等于的位置，
改造一下，这个题可以找target大于mid-1小于等于mid就可以了。返回这个mid
如果target比nums[0]还小，直接返回0，如果比nums[-1]还大，直接返回len(nums)

解决方案1：

class Solution:
    def searchInsert(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        for i,v in enumerate(nums):
            if v >= target:
                return i
        return len(nums)

解决方案2：

class Solution:
    def searchInsert(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        if target > nums[-1]:
            return len(nums)
        if target <= nums[0]:
            return 0
        start = 0
        end = len(nums) - 1
        while start <= end: # 二分
            mid = (start + end) // 2
            if nums[mid] >= target:
                if nums[mid-1] < target:
                    return mid
                else:
                    end = mid - 1
                    continue
            else:
                start = mid + 1
                continue

53 五十三 ： 最大子序和
问题描述：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例：

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

问题分析：

这题一看挺懵的，甚至还想到了分治。其实这题有很简单的写法(**在线处理**)，O(n)的。分治的待会儿试试。
啥叫在线处理？就是你程序别管在哪停下，都是当前的最优解。
最大子序列和，连续元素相加和最大的那一部分的和。
怎么求呢？先好好的理清思路：
负数肯定是会减益的，正数肯定是会增益的。
由此可以想到是不是可以找到正数聚集区？
后来想了想，这种办法不靠谱。为啥呢？ 请看例子：
[-1,-1,100,-2,-2] 肯定比 [1,1,1,2,2] 大。所以说抛开剂量谈毒性都是耍流氓。所以这条路走不通。

然后还是回到刚才总结的那个思路：
负数肯定是会减益的，正数肯定是会增益的。
而且最大子序和说不定在哪，需要设置一个max进行暂存。然后设置一个temp对当前子序列和进行暂存，
如果某个temp对后面的元素产生了减益，就要摒弃；每次都判断temp大还是max大，如果temp比max还大，
就得更新max的值。
为什么每次都要判断？
因为你不知道当前子序列和和max的关系。
比如5,4,3,2,-3,4   到-3的时候，虽然-3是减益的，你的temp没有更新给max。但是整个temp的
值是正的，对后面的元素4来讲，temp是增益的。也就是说，temp虽然一时比max小了，但是它只要对于
后面的元素来讲还是增益的，就有可能东山再起超过max.所以对于这种不确定状况，只能每次都判断。
为什么temp对后面的元素产生了减益就要摒弃？
想想看吧，一颗老鼠屎坏了一锅粥。加了老鼠屎的粥好呢，还是不加好呢？

解决方案1：O(n)

class Solution:
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        temp = 0 # temp用来暂存当前子序列的和
        max_sub_sum = nums[0]
        for i in nums:
            temp += i
            if temp > max_sub_sum: # 如果当前子序列的和大于最大子列和，就更新值
                max_sub_sum = temp
            if temp < 0: # 如果是老鼠屎，就把他摒弃掉
                temp = 0
        return max_sub_sum

思路2：分治求解

分治的总思想如下：
最大子列和要么出现在左边的子列，要么出现在右边的子列，要么出现在跨中间的子列之中。
然后不断的递归求解就可以了。每次递归都返回自己这个小子列中的最大子列和。
总之，一定要各司其职。出现在左边的子列，就一定是只找左边的子列中的最大子列和，出现在右面
就是找右面的最大子列和，出现在中间，就是将左面在线处理和右面在线处理的和加起来。
每次都比较到底左面大还是右面大还是中间大，只返回最大的。
分治的时间复杂度是O(nlogn)  不如在线处理

解决方案2：

class Solution:
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        def divede(left,right):
            if left == right: # 如果到底部了，就直接返回，因为它自己就是
                return nums[left] # 最大子列和

            center = (left + right)//2 # 中线
            max_left = divede(left,center) # 递归求左子列的最大子列和
            max_right = divede(center+1,right) # 求右子列的最大子列和

            # 开始求中间的最大子列和
            max_ll = nums[center] # 将中间开始第一个元素设置成当前最大子列和
            # 借鉴的在线处理的思想
            templ = 0 # 当前的子列和，初始化为temp
            for i in range(center,left-1,-1):
                templ += nums[i]
                if templ > max_ll: # 求出左边从中间向左最大的'子列和'
                    max_ll = templ

            max_rr = nums[center+1] # 跟上面一个道理，注释懒得写了
            tempr = 0
            for i in range(center+1,right+1):
                tempr += nums[i]
                if tempr > max_rr:
                    max_rr = tempr
            return max(max_left,max_right,max_ll + max_rr) # 谁大就返回谁
        res = divede(0,len(nums)-1)
        return res

58 五十八：最后一个单词的长度
题目描述：

给定一个仅包含大小写字母和空格 ' ' 的字符串，返回其最后一个单词的长度。

如果不存在最后一个单词，请返回 0 。

说明：一个单词是指由字母组成，但不包含任何空格的字符串。

示例：

输入: "Hello World"
输出: 5

思路：

我已经彻底变成一个pythoner了。。
首先想到的是strip()  然后split()一下，如果split出来的列表长度是0 就返回0
如果列表长度不为0，就返回最后一个元素的长度

然而，要自己装个B，
从字符串末尾开始往前扫描，如果遇到空格且还没有扫描到任何单词就跳过，遇到空格且已经扫描过一个单词了
就返回单词长度。 如果没遇到空格，就自增一下单词的长度值。

解决方案1：

class Solution:
    def lengthOfLastWord(self, s):
        """
        :type s: str
        :rtype: int
        """
        if not s:
            return 0
        k = s.strip()
        l = k.split()
        if len(l):
            return len(l[-1])
        return 0

解决方案2：

class Solution:
    def lengthOfLastWord(self, s):
        """
        :type s: str
        :rtype: int
        """
        temp = 0
        for i in s[::-1]:
            if i == ' ':
                if temp:
                    return temp
                else:
                    continue
            temp += 1
        return temp

66 六十六：加一

题目描述：

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储一个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例：

输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。
输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。

思路：

这题可以从末尾开始遍历，是9的话，变成0，继续往前判断。
不是9的话，直接+1 返回列表。
如果第一个元素得变成0，那肯定是进位了，需要assert一个1在0号元素的位置。

解决方案：

class Solution:
    def plusOne(self, digits):
        """
        :type digits: List[int]
        :rtype: List[int]
        """
        for i in range(len(digits)-1,-1,-1):
            temp = digits[i]
            if i == 0 and temp == 9:
                digits[i] = 0
                digits.insert(0,1)
                break
            if temp == 9:
                digits[i] = 0
            else:
                digits[i] = temp + 1
                break
        return digits

67 六十七：二进制求和
题目描述：

给定两个二进制字符串，返回他们的和（用二进制表示）。

输入为非空字符串且只包含数字 1 和 0。

题目示例：

输入: a = "11", b = "1"
输出: "100"
输入: a = "1010", b = "1011"
输出: "10101"

思路：

从末尾开始相加，判断有没有进位，设置temp为进位
还要注意哪个串长一些。
先按短串的长度遍历，遍历完了看一下temp的值，如果temp是0，则直接加上长串的未遍历部分。
如果temp不是0  接着遍历长串的剩余部分。

但是，这样做效率极低。身为一个地地道道的python程序员，这样做很low的。
可以通过int来做这个事儿，有两种写法

解决方案1：

class Solution:
    def addBinary(self, a, b):
        """
        :type a: str
        :type b: str
        :rtype: str
        """
        l = a if len(a) > len(b) else b
        if l == b:
            a,b = b,a
        # a是长串
        temp = 0
        res = ''
        for i in range(-1,-len(b)-1,-1):
            t = eval(a[i]) + eval(b[i]) + temp
            if t == 3:
                res = '1' + res
                temp = 1
            elif t == 2:
                res = '0' + res
                temp = 1
            elif t == 1:
                res = '1' + res
                temp = 0
            else:
                res = '0' + res
        if not temp: # 如果没进位，拼接后直接返回
            res = a[:len(a)-len(b)] + res
            return res
        for i in range(-len(b)-1,-len(a)-1,-1): # 否则就接着遍历剩余部分
            t = temp + eval(a[i])
            if t == 2:
                res = '0' + res
                temp = 1
            elif t == 1:
                res = '1' + res
                temp = 0
            else:
                res = '0' + res
        if temp:
            res = '1' + res
        return res

解决方案2：

class Solution:
    def addBinary(self, a, b):
        """
        :type a: str
        :type b: str
        :rtype: str
        """
        a = int(a,base=2)
        b = int(b,base=2)
        k = str(bin(a+b))
        return k[2:]

解决方案3：

class Solution:
    def addBinary(self, a, b):
        """
        :type a: str
        :type b: str
        :rtype: str
        """
        return bin(int(a, 2) + int(b, 2))[2:]

69 六十九 ： x的平方根

题目描述：

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例输出：

输入: 4
输出: 2
输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

思路：

没啥思路。。直接x**0.5然后取个整

实现代码：

class Solution:
    def mySqrt(self, x):
        """
        :type x: int
        :rtype: int
        """
        return int(x**0.5)

70 七十 ： 爬楼梯

问题描述：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶
输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

题目分析：

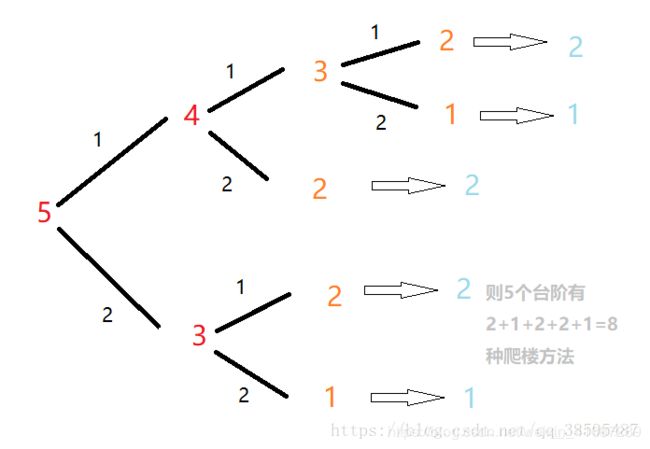
这题看了两眼我就懵逼了。甚至还想到了排列组合。
正当我犯愁为啥脑袋这么笨的时候，倔劲儿上来了=-=
多写了几项发现这货怎么这么像斐波那契数列。
emmmm.... 这事儿就好办了。刚用动归写过斐波那契。
然后就好奇为啥这货是一个斐波那契额呢？？？
后来想了想，比如5为例，登上第五级台阶时，有可能是从第三级台阶一下迈了2阶上来的，
也有可能是从第四级台阶一下迈了1阶上来的，而以此类推，第三级和第四级也是这么来的，
所以这是个斐波那契数列是一点毛病都没有的。
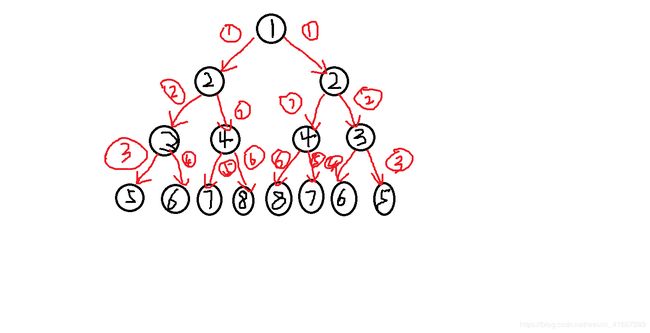
我还盗了个大神的图

解决方案1（非递归式）：

class Solution:
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        a = 1
        b = 2
        while n > 1:
            n -= 1
            a,b = b,a+b
        return a

解决方案2（隐式地运用了动归的递归式）：

class Solution:
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """

        def stairs(a, b, n):
            if n > 1:
                return stairs(b, a + b, n - 1)
            return b

        return stairs(1, 1, n)

解决方案3 备查技术的动归解法：

class Solution:
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        res = [-1 for i in range(n+1)]
        def quee(n):
            if res[n] != -1:
                return res[n]
            if n == 1:
                val = 1
            elif n == 2:
                val = 2
            else:
                val = quee(n-1) + quee(n-2)
            res[n] = val
            return val
        return quee(n)

83 八十三：删除排序链表中的重复元素

问题描述：

给定一个排序链表，删除所有重复的元素，使得每个元素只出现一次。

示例：

输入: 1->1->2
输出: 1->2
输入: 1->1->2->3->3
输出: 1->2->3

思路：

如果是第一个元素，就不处理，将其暂时用temp存起来
如果不是第一个元素，就判断是不是与上一个元素temp相等，如果相等就删除当前元素.另外
更新t的值。不需要更新temp的值，因为你不知道更新后的t值是不是还跟temp相等。
如果不与上一个元素temp相等，就分别更新temp的值和t的值，不断的循环下去。

这样做是一个常见的思路，但是这样会略嫌麻烦，因为如果一串1是挨着的，为啥还要一个一个的删除？
直接删掉一串不是更方便？
所以有了改进算法。
设置一个flag值来判断到底是不是相等。如果相等则置flag为True. 循环下去，直到不满足条件跳出循环。
如果flag为True,证明进入过while循环，也就是说有重复的元素，那就删除重复元素。下面还判定了t的值来
判断是不是要更新temp和t。

解决方案1：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def deleteDuplicates(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        temp = None
        flag = False
        t = head
        while t:
            if t == head:
                temp = t
                t = t.next
                continue
            if t.val == temp.val: # 相等则删除当前元素
                temp.next = t.next
                t = t.next
            else:
                temp = t
                t = t.next
        return head
s = Solution()
print(s.deleteDuplicates())

解决方案2(优化)：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def deleteDuplicates(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        temp = None
        flag = False
        t = head
        while t:
            if t == head: # 跳过开头
                temp = t
                t = t.next
                continue
            while t and t.val == temp.val:
                flag = True
                t = t.next
            if flag: # 如果进入过while循环
                temp.next = t
                flag = False
            if t: # 判断t
                temp = t
                t = t.next
        return head

88 八十八： 合并两个有序数组

问题描述：

给定两个有序整数数组 nums1 和 nums2，将 nums2 合并到 nums1 中，使得 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。

示例：

输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

输出: [1,2,2,3,5,6]

思路：

原本想
nums1.extend(nums2)
nums1.sort()
呢。
结果发现这题的坑爹之处在于，它把nums1开的非常大，而且给你置了很多0元素。
没办法，只能用下面的代码解决了。
其实这题还能用二分来做。
思路：
遍历nums2, 为nums2的每个元素寻找插入位置。  
将nums2的每一个元素都置为target，在nums1中用二分寻找插入位置。
代码就不写了。人生苦短，我用python.

解决方案：

class Solution:
    def merge(self, nums1, m, nums2, n):
        """
        :type nums1: List[int]
        :type m: int
        :type nums2: List[int]
        :type n: int
        :rtype: void Do not return anything, modify nums1 in-place instead.
        """
        nums1[m:] = nums2
        nums1.sort()

100 一百：相同的树

问题描述：

给定两个二叉树，编写一个函数来检验它们是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例：

思路：

用的是先序遍历。
flag初始化为True,如果a结点和b结点元素不相同，或者一个空一个非空，就置为False
然后递归遍历左子树，再递归遍历右子树。

也可以直接把题目给的函数当作递归函数来做。 

解决方案1：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSameTree(self, p, q):
        """
        :type p: TreeNode
        :type q: TreeNode
        :rtype: bool
        """
        flag = True
        def bianli(p,q):
            nonlocal flag
            if p and q:
                if p.val != q.val:
                    flag = False
                else:
                    bianli(p.left,q.left)
                    bianli(p.right,q.right)
            else:
                if q != p:
                    flag = False
        bianli(p, q)
        return flag

解决方案2：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSameTree(self, p, q):
        """
        :type p: TreeNode
        :type q: TreeNode
        :rtype: bool
        """
        if(p==None and q==None):
            return True
        if(p==None):
            return False
        if(q==None):
            return False
        if(p.val==q.val):
            return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
        else:
            return False

第三种解决方案：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSameTree(self, p, q):
        """
        :type p: TreeNode
        :type q: TreeNode
        :rtype: bool
        """
        if p and q:
            if p.val != q.val:
                return False
            else:
                return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
        elif p != q:
            return False
        return True

101 一百零一 ： 对称二叉树

题目描述：

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

示例：

思路：

一开始想着这不直接比较左子树等于右子树就可以了嘛？？？
然后事实证明我脑子笨=-=
后来想了想，欸？？我先反转其中一颗子树，然后比较两颗子树不就可以了吗？？
然后又引入了一个新的问题，反转二叉树=-=
后来又想了想，可以层序遍历呀。
分别层序遍历左子树和右子树，看看每一层的列表是不是镜像的不就OK了吗？
于是  迭代方法出来了。。

至于递归的话，没啥好说的。比较方法是一样的。只不过是用递归做的。
画个时序图。总之，就是从两侧往中间比，只不过是递归的写法。图可能有点错=-=但是不想改了。

代码1(迭代)：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        nextsl = [] # 存放左子树每一层的列表
        nextsr = [] # 存放右子树每一层的列表
        if root:
            nextsl.append(root.left)
            nextsr.append(root.right)
        else:
            return True
        while len(nextsl) or len(nextsr):
            if len(nextsl) != len(nextsr): # 如果长度都不相等肯定不是镜像的
                return False
            lenth = len(nextsl)
            for i in range(lenth):
                if nextsl[i] is None and nextsr[lenth-i-1] is not None:
                    return False
                elif nextsr[i] is None and nextsl[lenth-i-1] is not None:
                    return False
                elif nextsl[i] is not None and nextsr[lenth-i-1] is not None and nextsl[i].val != nextsr[lenth-i-1].val:
                    return False
            newsl = []
            newsr = []
            for i in range(lenth):
                if nextsl[i]:
                    newsl.append(nextsl[i].left)
                    newsl.append(nextsl[i].right)
                if nextsr[i]:
                    newsr.append(nextsr[i].left)
                    newsr.append(nextsr[i].right)
            nextsl = newsl # 更新左子树列表的值
            nextsr = newsr # 更新右子树列表的值
        return True

代码2(递归)：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSymmetric(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        def ist(left,right):
            if left == None and right == None: return True;
            if left == None and right != None: return False;
            if left != None and right == None: return False;
            
            return left.val == right.val and ist(left.left,right.right) and ist(left.right,right.left)
        
        if(root == None): return True;
        return ist(root.left,root.right)

104 一百零四：二叉树的最大深度

问题描述：

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

思路：

如果当前结点不是None, 就代表这层存在,所以最大深度应该是1+它的左子树和右子树中最深的那一个值
所以深度应该+1，然后继续往下递归。
如果当前结点是None,就代表这层不存在，直接返回0就可以了。

解决方案：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None:
            return 0
        l = self.maxDepth(root.left)
        r = self.maxDepth(root.right)
        if l > r:
            return 1 + l
        else:
            return 1 + r

107 一百零七 ： 二叉树的层次遍历II

问题描述：

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，
逐层从左向右遍历）

示例：

解题思路：

1、运用非递归式的层序遍历，添加到res列表中然后将res列表反转。
     这样的话需要设置一个last列表，存放刚刚遍历过去的那一层。从last更新current，然后current被遍历
     过后又变成了last
     还要设置一个data列表，用来暂存某层的值。
     不要忘记last的边界条件，如果last为空，就没有进行下去的必要了。
     如果data为空，就没有添加到res中的必要了（这也意味着循环要结束了。因为data为空current必为空
     如果current是空，它变成last也是空）
     一定要注意边界条件。

2、递归
	递归的话需要一个值来表明这是哪一层的。所以需要两个参数，一个结点，一个深度
	如果是符合深度的，就加入相应深度的子列表。
	如果结点是空，直接return掉，因为我们不用return后的值。因为我们是在更新res

解决方案1： 非递归的层次遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def levelOrderBottom(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        if root is None: # 如果树根都没有，直接返回[]
            return res
        last = [root]
        res.append([root.val])
        while len(last): # 层序遍历
            current = []
            data = []
            for i in last: # 更新current和data的值
                if i.left is not None:
                    current.append(i.left)
                    data.append(i.left.val)
                if i.right is not None:
                    current.append(i.right)
                    data.append(i.right.val)
            if data:
                res.append(data)
            last = current
        return res[::-1]

解决方案2：层序遍历的递归解法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def levelOrderBottom(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        if root is None:
            return res
        def depth(root): # 求深度
            if root is None:
                return 0
            else:
                l = depth(root.left)
                r = depth(root.right)
            if l > r:
                return l + 1
            else:
                return r + 1

        def level(root,depth):
            if root is None: # 为空终止递归
                return
            res[depth-1].append(root.val) # 加入对应深度的列表
            level(root.left,depth-1)
            level(root.right,depth-1)


        depthh = depth(root) # 拿到最大深度
        for i in range(depthh): # 初始化res
            res.append([])
        level(root,depthh)
        return res

111 一百一十一：二叉树的最小深度

问题描述：

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例：

思路：

这题。。犯二了。没仔细看题目。
人家定义的最小深度是从根结点到最近的叶子结点的最短路径上的结点数量。
结果我一顿操作猛如虎，交上去收获了WA。因为我直接用的求最大深度模板，这样是不对的。这样求出来
的不一定是叶子结点。
还是老老实实用层序遍历来吧，如果某结点的左右孩子结点都是None,证明它是一个叶子结点，终止循环。

解决方案：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None: # 如果根结点都没有 返回0
            return 0
        cengci = [root]
        cont = 0
        while cengci != []: # 层序遍历不为空的话继续遍历
            cont += 1 # 层次+1
            nexts = [] # 临时存储下一层
            flag = False
            for i in cengci:
                if i.left is None and i.right is None:
                    flag = True
                if i.left is not None:
                    nexts.append(i.left)
                if i.right is not None:
                    nexts.append(i.right)
            if flag: # 如果发现某层出现了叶子，就退出循环
                break
            cengci = nexts # 更新层次列表
        return cont

112 一百一十二 路径总和

问题描述：

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例：

思路：

今天点儿背啊。刚做过一个叶子结点的，这不又掉沟里了。
只不过这次是用递归实现的。
如果一个结点是叶子结点，就看看到它这儿和是不是和target相同。
相同就输出True

解决方案：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def hasPathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: bool
        """
        if root is None:
            return False
        flag = []
        def find(root,current):
            if root is not None:
                if root.left is None and root.right is None: # 如果是叶子
                    if current + root.val == sum:
                        flag.append(True)
                current += root.val
                if root.left is not None:
                    find(root.left,current)
                if root.right is not None:
                    find(root.right,current)
        find(root,0)
        if len(flag):
            return True
        return False

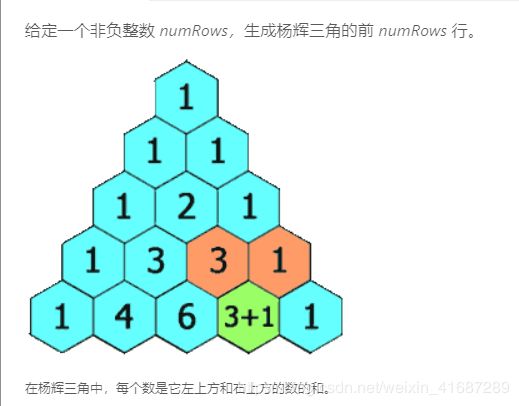
118 一百一十八 ： 杨辉三角

问题描述：

示例：

思路：

遍历上一层，更新本层值，然后本层再append一个1。加入res列表即可

解决方案：

class Solution:
    def generate(self, numRows):
        """
        :type numRows: int
        :rtype: List[List[int]]
        """
        if numRows == 0:
            return []
        if numRows == 1:
            return [[1]]
        res = [[1],[1,1]]
        for i in range(2,numRows):
            temp = [1]
            for j in range(1,i):
                temp.append(res[i-1][j-1] + res[i-1][j])
            temp.append(1)
            res.append(temp)
        return res

119 一百一十九 杨辉三角II

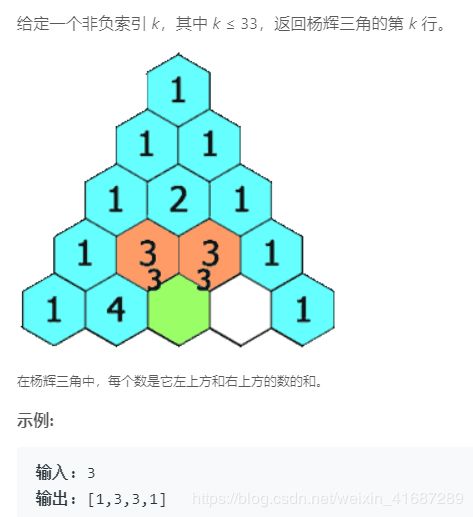
问题描述：

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

示例：

思路：

既然不让从上一行来求得，那就从自身求，或者看看有没有别的办法。
然后搜索了一下杨辉三角。
来自百度：
杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。
帕斯卡（1623----1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。
杨辉三角是中国古代数学的杰出研究成果之一，它把二项式系数图形化，
把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

直接上图：

根据这个性质，得知每次都要求组合数。
但是每次都求组合数实在是太慢了。
我发现组合数的公式是上图。
n的阶乘可以只算一次，m的阶乘每次都要算，n-m的阶乘每次也都要算，因为m的值是可变的。
这样写虽然可以做到题目的要求，空间复杂度为O(k)，但是真的好慢。
那怎么优化一下呢？
m的范围是从0到n//2   n-m的范围是从n到n//2
可以从这儿做文章，避免重复的阶乘运算。（设置两个变量，n,n_m）

解决方案1（空间复杂度O(2k)）：

class Solution:
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        if not rowIndex:
            return [1]
        rowIndex += 1
        def get_jiecheng(nums):
            if not nums:
                return 1
            res = 1
            for i in range(2,nums + 1):
                res *= i
            return res
        l = rowIndex*[1]
        n_s = get_jiecheng(rowIndex-1)
        temp = [x for x in range(1,rowIndex)]
        m = 1
        n_m = n_s//(rowIndex-1)
        for i in range(1,rowIndex-1):
            l[i] = n_s // (m * n_m)
            m *= temp[i]
            n_m //= temp[-i - 1]
        return l

解决方案2（空间复杂度O(k) 但是要把for遍历完）：

class Solution:
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        if not rowIndex:
            return [1]
        rowIndex += 1
        def get_jiecheng(nums):
            if not nums:
                return 1
            res = 1
            for i in range(2,nums + 1):
                res *= i
            return res
        l = rowIndex*[1]
        n_s = get_jiecheng(rowIndex-1)
        m = 1
        n_m = n_s//(rowIndex-1)
        for i in range(1,rowIndex - 1):
            l[i] = n_s // (m * n_m)
            m *= (i+1)
            n_m //= (rowIndex-i-1)
        return l

解决方案3（空间复杂度略大于O(k) 但是省一半的计算）：

class Solution:
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        if not rowIndex:
            return [1]
        rowIndex += 1
        if rowIndex == 2:
            return [1,1]
        def get_jiecheng(nums):
            if not nums:
                return 1
            res = 1
            for i in range(2,nums + 1):
                res *= i
            return res
        l = rowIndex*[1]
        n_s = get_jiecheng(rowIndex-1)
        m = 1
        n_m = n_s//(rowIndex-1)
        for i in range(1,rowIndex//2 + 1):
            l[i] = n_s // (m * n_m)
            m *= (i+1)
            n_m //= (rowIndex-i-1)
        if rowIndex%2:
            temp = rowIndex//2 + 1
            k = l[:temp-1][::-1]
            l[temp:] = k
        else:
            temp = rowIndex//2
            l[temp:] = l[:temp][::-1]
        return l

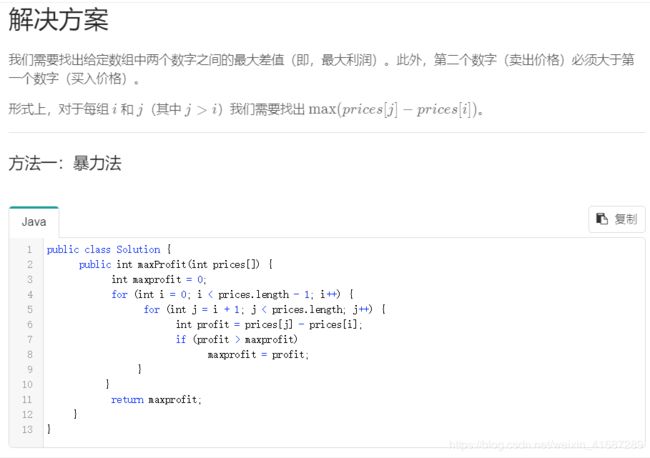
121 一百二十一 买卖股票的最佳时机

问题描述：

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例：

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
 
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

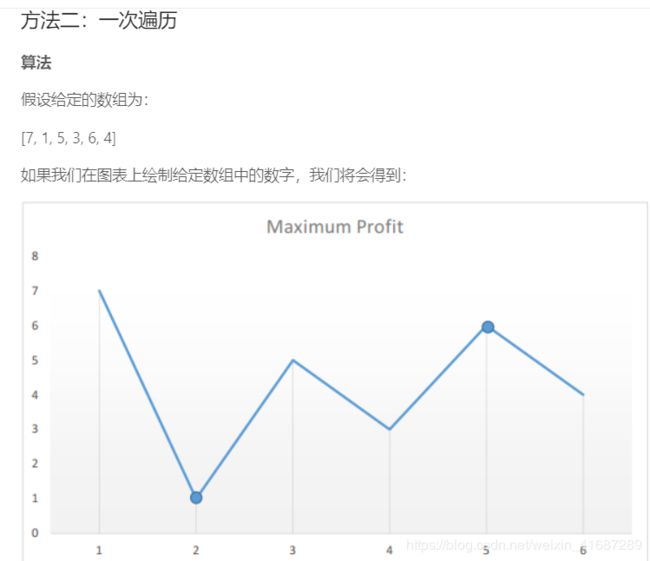
思路：

一个朴素的思路是从前往后遍历，每次都取出来剩余序列的最大值与当前值比较，作差。
复杂度为O(n^2) 太慢了。

怎么优化？可以从后往前遍历，设置maxs,max_temp,temp三个变量。
maxs用于存放当前子序列的最大值。max_temp用于存放后面子列最大值与当前值比较的最大的差值。
temp用于暂存后面子列最大值与当前值比较的差值，用于更新max_temp。

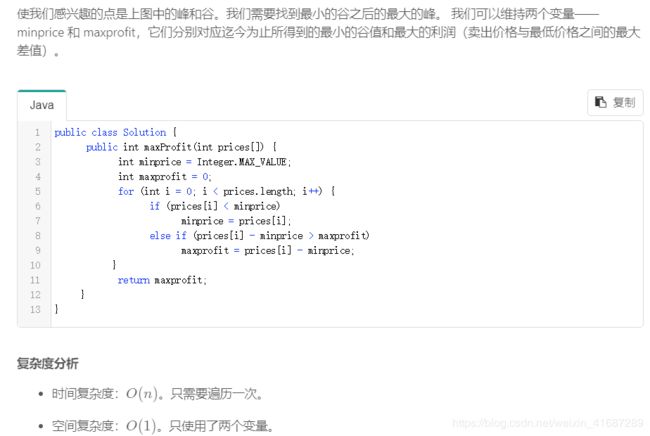
解决方案：

class Solution:
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        if not prices:
            return 0
        maxs = prices[-1]
        max_temp = 0
        for i in range(len(prices)-1,0,-1):
            if prices[i-1] > maxs:
                maxs = prices[i-1]
            else:
                temp = maxs - prices[i-1]
                if temp > max_temp:
                    max_temp = temp
        return max_temp

本题的官方题解：

122 一百二十二 买卖股票的最佳时机II

问题描述：

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例：

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
     输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

思路：

遇到递减序列的最后一个，设置为start
遇到递增序列的最后一个，设置为end
end - start 就是某一次的买入卖出。注意，卖出后应该更新start值（因为如果不及时更新start的话，
下一次的end-start会出错的。）。

解决方案：

class Solution:
    def maxProfit(self, prices):
        """
        :type prices: List[int]
        :rtype: int
        """
        # 局部最低时买入
        # 碰到局部最高时卖出
        if not prices:
            return 0
        lenth = len(prices)
        flag = False # 用于标识是否重新设置了start
        start = prices[0]
        sums = 0
        for i in range(lenth-1):
            if prices[i] > prices[i+1]:
                if not flag: # 如果没有重设start
                    continue
                else: # 如果重设了start 就该更新sums了。
                    sums += prices[i] - start
                    start = prices[i+1] # 重设start 因为start
                    # 要被初始化成剩余子列的第一个才合理
                    flag = False
            else:
                if not flag: # 重设start的值
                    flag = True
                    start = prices[i]
                else:
                    continue
        if prices[-1] - start > 0:
            return sums + prices[-1] - start
        return sums

125 一百二十五 验证回文串

问题描述：

给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。
说明：本题中，我们将空字符串定义为有效的回文串。

示例：

思路：

一种是循环一遍，把无关字符过滤掉，拿到res  判断res是不是回文
这种办法效率偏低。于是乎用空间换时间。
定义一个集合，过滤无关字符时用集合判断即可。

解决方案1（朴素）：

class Solution:
    def isPalindrome(self, s):
        """
        :type s: str
        :rtype: bool
        """
        if not s:
            return True
        res = ''
        for i in s:
            temp = ord(i)
            if (temp >= 48 and temp <= 57) or (temp >= 65 and temp <= 90):
                res += i
            elif temp >= 97 and temp <= 122:
                res += i.upper()
        if res == res[::-1]:
            return True
        return False

解决方案2 空间换时间：

class Solution:
    def isPalindrome(self, s):
        """
        :type s: str
        :rtype: bool
        """
        if not s:
            return True
        set1 = {'0','1','2','3','4','5','6',
                '7','8','9','a','b','c','d',
             'e','f','g','h','i','j','k','l','m','n',
             'o','p','q','r','s','t','u','v','w','x',
             'y','z'}
        s = s.lower()
        res = ''
        for i in s:
            if i in set1:
                res += i
        if res == res[::-1]:
            return True
        return False

136 一百三十六 只出现一次的数字

问题描述：

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例：

输入: [2,2,1]
输出: 1
输入: [4,1,2,1,2]
输出: 4

思路：

线性复杂度，不用额外空间，然后脑壳就破了。。
边打LOL边想，后来觉得其余元素出现两次是个坑，想到了异或
异或特性（对同一个数异或两次，结果不变）

解决方案：

class Solution:
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        res = nums[0]
        for i in nums[1:]:
            res ^= i
        return res

java版

class Solution {
    public int singleNumber(int[] nums) {
        int target = nums[0];
        for(int i = 1; i < nums.length; i++){
            target ^= nums[i];
        }
        return target;
    }
}

141 一百四十一 环形链表

题目描述：

给定一个链表，判断链表中是否有环。

进阶：
你能否不使用额外空间解决此题？

思路：

这题我首先想到的是怎么把走过的结点给标记一下。
然后我就写出了世界上最骚气的解决环形链表问题的代码=-=||！

然后想了想，有环的话，操场跑圈，跑的快的肯定能追上跑的慢的。于是乎写出了快慢指针解法。
无环的话，快指针肯定最先跑到尾部，所以这是一个退出条件。

解决方案1（史上最骚）：

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        while head:
            if head.val == 'bjfuvth':
                return True
            else:
                head.val = 'bjfuvth'
            head = head.next
        return False

解决方案2（快慢指针）：

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        if not head:
            return False
        slow = fast = head
        while slow:
            if fast.next is None or fast.next.next is None:
                return False
            if slow.next == fast.next.next:
                return True
            slow = slow.next
            fast = fast.next.next
        return False

155 一百五十五 最小栈

问题描述：

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) -- 将元素 x 推入栈中。
pop() -- 删除栈顶的元素。
top() -- 获取栈顶元素。
getMin() -- 检索栈中的最小元素。

示例：

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

思路：

乒乒乓乓一通写，当成个列表，用min求最小值。但是，常数时间找不到最小值，因为只能是O(n)。
这可咋办呢？
机智的我想到了用一个self.min来表示最小值，直接返回最小值不就好了？
但是这个方法有一个BUG，万一最后出栈的是最小值，该怎么更新最小值的值呢？又要用min吗？
这个问题这不是回到了问题原点了吗？
我又想到了可以通过一个pre_min 来存储之前的最小值。
然而这个并没有比刚刚的想法高明多少，万一把最小值和次小值都出栈了，那该怎么更新pre_min呢？
所以这个办法也不行，但是我们可以设置很多很多的pre_min   pre_pre_min啊？
对，这是个好办法，但是你不知道要弄多少个，而且会把自己完全弄晕。
所以说，在存储栈的时候就通过某种编码或者某种方式将当前的最小值存起来是最好的。出栈的时候，一查
就找出了当前的最小值，无需额外空间，而且是常数时间。

那，具体应该怎么做呢？
设置一个self.min，它的涵义是当前栈中的最小值。
每进来一个新元素，将它与self.min的差(为什么是差，一会儿说)压栈，如果这个差值小于0，证明它比压栈之
前的最小值还小，得更新一下最小值为它了。
如果要弹栈，首先看弹栈的元素是不是小于0，为啥呢？刚刚压栈的时候，是压的当前元素与之前栈的最
小值的差值，如果这个差值小于0，证明要弹栈的是最小的元素。所以弹出去之后应该更新最小值。
最小值怎么更新呢？别忘了，这个差值可是当前值与之前最小值的差，即，当前值-之前的最小值等于当前存放
在列表中的值。既然当前值等于最小值，所以 ，之前的最小值等于self.min - 当前存放在列表中的值，
就这样还原出了之前的最小值。这叫啥来着？？好像叫在线处理。
如果要取栈顶元素的话，还是看是不是小于等于0，如果当前放在列表中的值小于等于0的话，证明它是当前栈中
的最小值处理后的，所以直接返回最小值即可。
如果大于0，代表获取的并不是最小值，所以应该利用公式 当前值-之前的最小值=当前存放在列表中的值
将应该输出的值还原出来。

朴素解决方案1：

class MinStack(object):

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.L = []

    def push(self, x):
        """
        :type x: int
        :rtype: void
        """
        self.L.append(x)

    def pop(self):
        """
        :rtype: void
        """
        if len(self.L):
            self.L.pop()

    def top(self):
        """
        :rtype: int
        """
        if len(self.L):
            return self.L[-1]

    def getMin(self):
        """
        :rtype: int
        """
        if len(self.L):
            return min(self.L)
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()

改进后的解决方案2：

class MinStack(object):

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.L = []
        self.min = None

    def push(self, x):
        """
        :type x: int
        :rtype: void
        """
        if self.L == []:
            self.L.append(0)
            self.min = x
        else:
            self.L.append(x - self.min) # 将值减去进去之前的最小值
            if x < self.min:
                self.min = x
    def pop(self):
        """
        :rtype: void
        """
        if len(self.L):
            x = self.L.pop()
            if x < 0: # 如果出栈的是最小的元素，则更新最小值
                self.min = self.min - x
    def top(self):
        """
        :rtype: int
        """
        if len(self.L):
            x = self.L[-1]
            if x > 0: # 如果出栈元素不是最小值
                return x + self.min # 则将之还原为原来的x
            return self.min # 否则的话，自己就是最小值，直接返回最小值即可

    def getMin(self):
        """
        :rtype: int
        """
        return self.min
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()

160 一百六 相交链表

题目描述：

编写一个程序，找到两个单链表相交的起始节点。

示例：

思路：

这题的坑点在于，俩链表不一般长，你不知道该前进哪一个链表，该前进多少步才能判断
那咋办？截断。让他们俩一般长。
先遍历一遍两个链表，统计出他们的长度。
然后把长的链表从头截取多余的部分。
然后一起遍历这俩，如果结点相等就返回。

解决方案1（用集合）：

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def getIntersectionNode(self, headA, headB):
        """
        :type head1, head1: ListNode
        :rtype: ListNode
        """
        s = set()
        while headA:
            s.add(headA)
            headA = headA.next
        while headB:
            if headB in s:
                return headB
            headB = headB.next
        return None

解决方案2（用思路提到的）：

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def getIntersectionNode(self, headA, headB):
        """
        :type head1, head1: ListNode
        :rtype: ListNode
        """
        lenthA = lenthB = 0
        head_a = headA
        head_b = headB
        while headA or headB:
            if headA:
                lenthA += 1
                headA = headA.next
            if headB:
                lenthB += 1
                headB = headB.next
        if lenthB > lenthA:
            t = lenthB - lenthA
            while t:
                head_b = head_b.next
                t -= 1
        else:
            t = lenthA - lenthB
            while t:
                head_a = head_a.next
                t -= 1
        while head_a:
            if head_a == head_b:
                return head_a
            head_a = head_a.next
            head_b = head_b.next
        return None

167 一百六十七 两数之和 II - 输入有序数组

题目描述：

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:

返回的下标值（index1 和 index2）不是从零开始的。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例：

输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

思路：

可以用第一题的思路。
另外，也可以这样：
定住start元素，那么end元素越往左，和越小。
定住end元素，那么start元素越往右，和越大。
根据这个，可以写如果当前和大于target  定住start end往左。
反之，定住end  start往右

解决方案1：

class Solution:
    def twoSum(self, numbers, target):
        """
        :type numbers: List[int]
        :type target: int
        :rtype: List[int]
        """
        d = {}#按照键值对的方式存储数据 下标为值，真正的值为键
        for i in range(len(numbers)):
            if target - numbers[i] in d.keys():
                return [d[target-numbers[i]] + 1,i + 1]
            d[numbers[i]] = i

解决方案2：

class Solution:
    def twoSum(self, numbers, target):
        """
        :type numbers: List[int]
        :type target: int
        :rtype: List[int]
        """
        start = numbers[0]
        end = numbers[-1]

168 一百六十八 excel 表列名称

问题描述：

给定一个正整数，返回它在 Excel 表中相对应的列名称。

示例：

思路：

我不想说这题我想了好久=-= 好丢人
也不想说这题竟然是第一道秒掉所有人的题。。
总之，思路就是进制转换。除N取余法。
但是这可不是普通的除N取余法。根据171题的经验，这题是按权展开的逆过程。
所以要有借位的思想。如果整除掉了，余数是0，对应Z，这个Z哪来的？是从前面借来的。
所以商要减去1.

解决方案：

class Solution:
    def convertToTitle(self, n):
        """
        :type n: int
        :rtype: str
        """
        d = {
            1: 'A',
            2: 'B',
            3: 'C',
            4: 'D',
            5: 'E',
            6: 'F',
            7: 'G',
            8: 'H',
            9: 'I',
            10: 'J',
            11: 'K',
            12: 'L',
            13: 'M',
            14: 'N',
            15: 'O',
            16: 'P',
            17: 'Q',
            18: 'R',
            19: 'S',
            20: 'T',
            21: 'U',
            22: 'V',
            23: 'W',
            24: 'X',
            25: 'Y',
            0: 'Z',
        }
        res = ''
        while n:
            shang,yu = divmod(n,26)
            res = d[yu] + res
            n = shang
            if yu == 0: # 如果整除了
                n -= 1 # 就从前面借1位
        return res

169 一百六十九 求众数

题目描述：

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例：

输入: [3,2,3]
输出: 3
输入: [2,2,1,1,1,2,2]
输出: 2

思路：

先排序，拍完序后遍历一半的数组，看看当前元素是不是等于当前元素后面第lenth//2个元素，
如果相等，它就是众数。 时间复杂度比O(n^2)好，但是好不到哪里去。

后来想了想，一半以上的元素才叫众数，那肯定又有坑，不然干嘛不用数学中的众数呢。
不知道为啥想到了丝路英雄这个游戏=-=   我有比你多的兵，最后战斗完肯定我还剩下至少一个兵。
根据这个思想，设置了一个cont用于计数，temp用于标记当前看好的士兵。
如果士兵同归于尽了(cont = 0)，就重新设置一个temp和cont。
最后的temp一定是剩下的士兵(们)。
这个办法好像被人称为摩尔投票法=-= 在我看来是丝路英雄打仗法。

解决方案1(排序)：

class Solution:
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        nums.sort()
        lenth = len(nums)
        lenthh = lenth // 2
        res = None
        for i in range(lenth//2):
            if nums[i] == nums[i+lenthh]:
                res = nums[i]
        if res is None:
            res = nums[-1]
        return res

解决方案2(摩尔投票法)：

class Solution:
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        cont,temp = 0,0
        for i in nums:
            if cont == 0:
                cont += 1
                temp = i
            else:
                cont+=1 if i == temp else -1
        return temp

171 一百七十一 excel表列序号

问题描述：

给定一个Excel表格中的列名称，返回其相应的列序号。

示例：

思路：

这题显然是一个进制转换题。这不是一个彻头彻尾的26进制嘛。
先把str转成一个list，遍历就好了。

解决方案：

class Solution:
    def titleToNumber(self, s):
        """
        :type s: str
        :rtype: int
        """
        d = {
            'A': 1,
            'B': 2,
            'C': 3,
            'D': 4,
            'E': 5,
            'F': 6,
            'G': 7,
            'H': 8,
            'I': 9,
            'J': 10,
            'K': 11,
            'L': 12,
            'M': 13,
            'N': 14,
            'O': 15,
            'P': 16,
            'Q': 17,
            'R': 18,
            'S': 19,
            'T': 20,
            'U': 21,
            'V': 22,
            'W': 23,
            'X': 24,
            'Y': 25,
            'Z': 26,
        }
        l = list(s)
        res = 0
        for i in l:
            res = res*26 + d[i]
        return res

172 一百七十二 阶乘后的零

问题描述：

给定一个整数 n，返回 n! 结果尾数中零的数量。

示例：

输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.

还跟了个说明：

说明: 你算法的时间复杂度应为 O(log n) 。

思路：

求个阶乘复杂度都至少O(n)了，再加上判末尾0的时间。
很容易就呵呵哒。
记得小学老师讲过，只有末尾是0或者是5的倍数才有机会出0.
5想出0  要与2进行配对。
4 可以 出 2个2   6可以出一个，8可以出3个 ，所以说2的个数肯定比5的个数要多，所以只需要考虑
有多少个5.


    首先题目的意思是末尾有几个0
    比如6! = 【1* 2* 3* 4* 5* 6】
    其中只有2*5末尾才有0，所以就可以抛去其他数据 专门看2 5 以及其倍数 毕竟 4 * 25末尾也是0
    比如10！ = 【2*4*5*6*8*10】
    其中 4能拆成2*2  10能拆成2*5 
    所以10！ = 【2*（2*2）*5*（2*3）*（2*2*2）*（2*5）】
    一个2和一个5配对 就产生一个0 所以10！末尾2个0
    
    转头一想 2肯定比5多 所以只数5的个数就行了
    
    假若N=31 31里能凑10的5为[5, 2*5, 3*5, 4*5, 25, 6*5] 其中 25还能拆为 5**2 
    所以 里面的5的个数为 int(31/(5**1)) +  int(31/(5**2))

python的 n//5 可以做到这点，不断的除以5，得知有多少5.
对于能拆成多个5的，继续除下去，写成一个for循环即可。

解决方案：

class Solution:
    def trailingZeroes(self, n):
        """
        :type n: int
        :rtype: int
        """
        cont = 0
        while n:
            n //= 5
            cont += n
        return cont

189 一百八十九 旋转数组

问题描述：

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

示例：

输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释: 
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

思路：

1认怂，一个一个的移位
2可以先把前l-k个元素反转，再把后面k个元素反转 最后把整个列表反转
3可以直接切片

1的方法太2B就不写了。

解决方案1：

class Solution:
    def rotate(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: void Do not return anything, modify nums in-place instead.
        """
        def zhuanhuan(l,start,end):
            lenth = end - start
            for i in range(lenth//2):
                l[start+i],l[end-i-1] = l[end-i-1],l[start+i]
        lenth = len(nums)
        if k > lenth:
            k %= lenth
        zhuanhuan(nums,0,lenth-k)
        zhuanhuan(nums,lenth-k,lenth)
        zhuanhuan(nums,0,lenth)

解决方案2：

class Solution:
    def rotate(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: void Do not return anything, modify nums in-place instead.
        """
        l = len(nums)
        k %= l
        nums[0:l] = nums[l-k:]+nums[:l-k]

190 一百九 颠倒二进制位

问题描述：

颠倒给定的 32 位无符号整数的二进制位。

示例：

输入: 43261596
输出: 964176192
解释: 43261596 的二进制表示形式为 00000010100101000001111010011100 ，
     返回 964176192，其二进制表示形式为 00111001011110000010100101000000 。

思路：

这题很坑的=-=注意自己补全32位。用python内置的写了下。
用位运算写了下。

解决方案1：

class Solution:
    # @param n, an integer
    # @return an integer
    def reverseBits(self, n):
        t = bin(n)[2:]
        l = len(t)
        lenth = 32 - l
        pre = '0'*lenth
        true = (pre + t)[::-1]
        res = int(true,2)
        return res

解决方案2：

class Solution:
    # @param n, an integer
    # @return an integer
    def reverseBits(self, n):
        res = 0
        for i in range(32):
            res<<=1 # 将res向左移位
            res += n&1 # n&1是取最后一位
            n>>=1 #n向右移位，确保取的是最新的一位
        return res

191 一百九十一 位1的个数

问题描述：

编写一个函数，输入是一个无符号整数，返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

示例：

输入: 11
输出: 3
解释: 整数 11 的二进制表示为 00000000000000000000000000001011
输入: 128
输出: 1
解释: 整数 128 的二进制表示为 00000000000000000000000010000000

思路：

可以用普通的除二取余法 但是懒得写了。
写一点pythonic的东西吧。

解决方案1：

class Solution(object):
    def hammingWeight(self, n):
        """
        :type n: int
        :rtype: int
        """
        b = bin(n)[2:]
        cont = 0
        for i in b:
            if i == '1':
                cont += 1
        return cont

解决方案2：

class Solution(object):
    def hammingWeight(self, n):
        """
        :type n: int
        :rtype: int
        """
        return bin(n).count('1')

198 一百九十八 打家劫舍

问题描述：

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例：

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

思路：

这题首先想到了动态规划。
分成两种情况。第一个是，拿了i，但是不能拿i+1
				第二个是 拿了i+1 但是不能拿i
将原问题分割成子问题，子问题的最优决策可以导出原问题的最优决策。
现有两种可能情况，当前房屋抢和当前房屋不抢。若当前房屋抢，则下一房屋不能抢；
若当前房屋不抢，则下一房屋可抢；
sum[i]=max(sum[i-1],sum[i-2]+nums[i])
sum[0]=nums[0];
sum[1]=max(nums[0],nums[1]);

解决方案：

class Solution(object):
    def rob(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not len(nums):
            return 0
        if len(nums) == 1:
            return nums[0]

        sums = [0]*len(nums)
        sums[0] = nums[0]
        sums[1] = max(nums[0],nums[1])
        for i in range(2,len(nums)):
            sums[i] = max(sums[i-1],sums[i-2]+nums[i])
        return sums[-1]