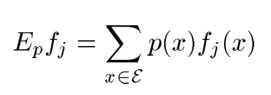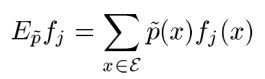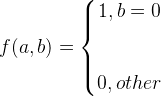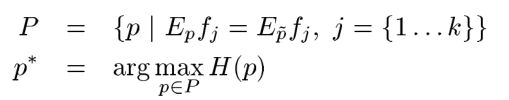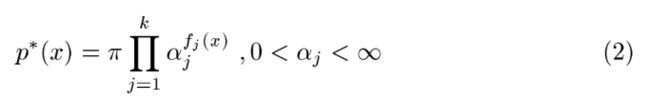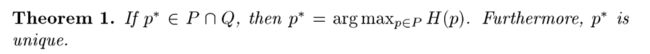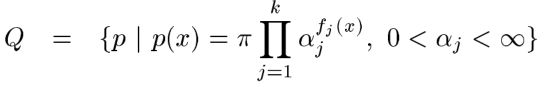NLP --- 最大熵模型的引入

前几节我们详细的阐述了什么是HMM,同时给出了HMM的三个问题，也给出了解决这三个问题的方法最后给出了HMM的简单的应用。其中为了解决第三个问题我们引入了EM算法，这个算法有点麻烦，但是不难理解，而解决第一个和第二个问题时使用的算法基本上都是基于动态规划的，这里需要大家首先对动态规划算法有深入的理解，这样才有可能理解前向、后向和维特比算法，所所以从这里可以看出一些基础性的算法很重要。前面基本就讲了这么多，今天我们将进入下一个核心点，也是最难的部分了，一旦这个难点解决了，后面的就很容易了，像分词呀、词性标注呀等等都是他们的应用，因此这里我们都需要好好理解，我会尽最大的努力打他们写的通俗易懂，看到这篇文章的同学建议多找几本书结合者理解，争取深入理解他们，一旦深入理解。这样的方法不仅仅可以应用到自然语言处理中，也可以用在其他方面，以后如果我们现实中遇到类似的问题能想到这样的类似的方法可以解决，这是最重要的能力，好，下面就说下面好多节的内容安排，首先是先介绍最大熵模型，然后再介绍条件随机场CRF，这两个算法的关系和EM与HMM算法是类似的，也就是说条件随机场的解决思路和最大熵模型很类似，讲这两个算法会引入很多的基础算法，这里我们都会详细讲解的，好，到这里我们就开始今天内容了即最大熵模型。

什么是熵

熵在统计物理中用亍度量一个热力学系统的无序程度。热力学第二定律，又称“熵增定律”，表明了在自然过程中，一个孤立系统的总混乱度（即“熵”）不会减小。也就是说在一个封闭的系统中，这个系统的熵只会越来越大，而不会越来越小。

例如有一堆钢铁，在没有人为的参与时，他只会随着时间的而风化为尘土而不会变为超强战斗机，这里风化为尘土就是钢铁有序的状态变为更混乱的无序状态了，而超强战斗机会更有序此时熵会减少，然而钢铁不会自动变为超强战斗机的。

在举一个例子，如一滴蓝色墨水滴入清水中，随着时间的流逝墨水逐渐和清水混合一起并达到了稳定的状态，这也是熵增的原理了，因为刚开始时，墨水中并没有掺有清水，墨水里都是墨水就一种状态即墨水，但是当滴入水中时墨水中逐渐参加水了，因此开始混乱起来，因此熵是增加的。

在举一个例子，假如人类多年后灭绝了，那么在地球上建造的有序的建筑，会随着时间不断的风化，大约5万年左右，地球上人类生存的迹象既不会存在，这也是熵增原理，因为建筑相对来说是比较有序的，但是风化后会的很无序这就是熵增了。

上面的三个例子详细大家应该知道什么是熵，什么是熵增了吧，其实熵就是描述事物的无序化程度的衡量指标，这里需要大家好好体会理解一下。我觉如果大家理解上面的内容了，那基于熵的决策树应该也理解了，刚开始还没分类时，数据很混乱，所以熵很大，但是通过一次分类后，从无序开始变的有序了，随着分类不断的进行，数据越来越有序，因此熵会越来越小，而熵增模型是怎么定义的呢？这里我把决策树那篇文章的熵增定义直接拿过来，有兴趣的可以看看我的那篇文章：信息增益理解起来其实很简单，未经分类的数据是无序化、不确定的也就是熵最大的时候，此时的熵使用表示，如果根据某一个特征A进行分类后数据的熵为，此时的熵比要小，因为分为某一类后数据开始有序化了或者确定了，那么定义信息增益为：

                                

由上面的解释可知信息增益其实就是通过数据分类后，数据的熵变低了（因为分类代表有序），而根据某个特征使熵降低了多少称为信息增益，强调一下增益的概念，其实是指数据通过这个特征有序化的程度即熵的变化量。

很容易理解决策树是如何工作的了吧，其实他就是根据哪个特征的分类后会使的熵增最大就使用哪个特征进行分类，大家学习时就这样，不停的和以前学的知识相联系，多思考多总结才能快速进步。

我们继续介绍另外一个关于熵的即信息论中的熵的定义：

在信息论中，熵被用来衡量一个随机变量出现的期望值。它代表了在被接收之前，信号传输过程中损失的信息量，又被称为信息熵。信息熵也称信源熵、平均自信息量。在1948年，香农将热力学的熵，引入到信息论，因此它又被称为香农熵。这里就不详细解释这个熵了，学习过通信原理的同学应该理解的很深入，简单来说我用多少二进制的位数来表示信息的状态。

具体是熵的定义这里就不讲了，请看我的这篇文章即决策树，下面就开始讲最大熵模型。

最大熵模型

在讲解最大熵原理之前，我们先回忆一下最大释然法，在最大释然法中，假如我们的样本满足一定的分布，但是该分布的一部分参数我们不知道，我想通过样本把这些参数给估算出来，现在我从样本抽样得到一个样本集，那么我如何通过样本集的概率去估算我们的未知参数呢？最大释然法的原理思想是这样的，就是这些未知参数应该使我抽到的样本概率是最大的，那么我们就可以解出这参数了，这就是最大释然法的原理思想，而最大熵模型的思想和其类似，但是不同的是他不是要求抽样出来的概率最大为指标了，下面我们就详细的看看，最大熵模型是在一一个不完整的分布中，他有些参数是已知的例如存在约束条件，而另一些参数是未知的，现在要求的是我应该如何求得这些未知的参数呢？最大熵的原理是，在满足已知条件（约束条件）的情况，未知条件应该使的这个分布的熵最大，这是和最大释然法的最根本的区别，最大释然是希望参数使的概率最大，而最大熵是使的整个分布的熵是最大的，这里大家应该好好理解一些他们的区别，下面给出最大熵的定义：

在只掌握关于未知分布的部分信息的情况下，符合已知知识的概率分布可能有多个，但使熵值最大的概率分布最真实地反映了事件的的分布情况，因为熵定义了随机变量的不确定性，当熵值最大时，随机变量最不确定，最难预测其行为。

这里在简要的解释一下，这是根据我们上面说的熵是描述混乱程度的指标，在未知分布的系统中，我们需要求他的分布，只需取一个熵值最大的那个分布就可以代表这个系统的分布，因为根据热力学可以知道，熵越大，则不确定性越高，随机性就越大，就越能代表系统的特性。那么最大熵和最大释然求出的分布会一样吗，这个需要看情况了，有时相等有时不同，因为他们的应用不同，所有结果不同，下面我们就看看最大熵模型是如何求解的。

这里需要先说明，我们根据一篇讲稿为主讲解最大熵模型的求解过程（点击这个可以下载，免费的），大家需要深入理解这个，然后我们在通过李航的书来看看现代的最大熵求解过程，其实是一样的只是表示上有些区别，好下面开始：

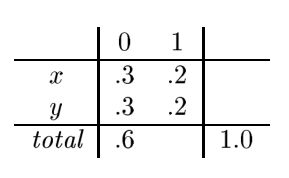
假如我有两个随机变量的联合概率密度，其中a可能取，b可能取0或者1，首先他们需要满足的条件是概率和为1，这是最基本的了，第二个约束就是在b=0的时候的概率总和为0.6，如上图所示，即：

                                   

问  ？的值应该为多少，其中的一种可能情况为：

上图的数据就满足要求，但是是不是最好的参数呢？即是不是达到熵最大呢？不一定，大家可以算一下熵的大小，这里使的熵最大的参数取值应该为如下所示：

通过计算后得到上面的参数，满足了两个约束，同时使的熵最大，我们发现x，y取0.6的均值就可以了，其他取0.6的均值就可以了，这不很简单吗？只有取均值就可了，有什么好计算呢？其实这是简单的情况，如果有多个变量多个约束你怎么分呢？所有还是需要一个计算的过程，那么上面的是怎么计算的呢？下面我们从最简单的例子开始讲起：

对于股市的变化，大家应该都有所耳闻，一般股市的变化都会和当年的各种情况有关，例如银行的利息、国家的政策、自然灾害等等特征都有关，假如有两个变量a，b分别代表两个特征， 其中b的特征很重要，例如一个公司的财务报表对将来的股市将有很大的影响，国家政策对股价也有很大的影响等等这样的特征很重要，而其他特征例如美国发生龙卷风导致颗粒无收，对我国的股市没啥影响，叙利亚继续战争对我国也没有影响等等这些就是不重要的特征。这里我们的b取值等于0是就是很重要的特征即，我们应该很关心这个特征是否被满足，而其他特征就不重要了，随便取值但是应该使的整个的熵达到最大，也就是说我们关心的必须满足要求，不关心的你可以任取但是必须使整个熵最大，这是我们的硬性条件，那么我们如何设计其他的特征的值呢？这里就需要引入一个特征函数，如下式：

其中：

                              

                              

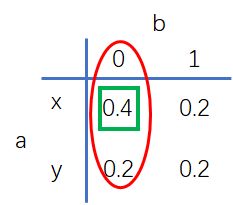
其中是特征函数是二值函数即要么为0要么为1，代表我们关心的什么，如上图的概率分布我们关心的b=0时的概率为0.6即第一列如上图的红色区域，那么使用特征函数来表示就是如下：

                             

如果我关注的是第一行，则只需要把b=0换成a=x即可，如果我关心的不是一行或者一列，而是关心某一个，例如0.4那个数位置如上图的绿色区域，此时只需要把b=0.换成b=0且a=x，一次类推，只有我们关心的都可以写出来，因此在我们实际使用中我们关心的不止一个，因此会有不同的特征组合函数,而所代表的就是我们关心的约束条件，上面的的定义是按照均值定义的，其实他是约束条件的概率相加，例如上面的第一列，大家按照公式可得，这里的P是加了“^”进行区别，而没加的代表我们将要设计的概率分布为也应该要满足约束，计算是一样的，所以（1）式很简单，这里大家应该理解而来把，在强调一下：

上式是我们比较看重的约束的表达，也可看重是均值，我们按照上图的概率矩阵转移，把b=0看做我们重要的特征，按照上式的表达方式写成 ，这就是约束条件了。而下面这个是我们需要设计的概率分布，和上面一样他也需要满足我们的要求。

所以（1）式表达的就这么简单，大家别晕了。我们继续往下看：

 

上面第一个式子是说我们要寻找的P要满足k个约束条件，下式说是在满足的约束的情况下，找到是熵值最大的那个P,这个也容易理解吧，我们继续往下：

这里需要强调的是的形式是什么样的呢？这里直接给了的结构是指数族的形式，如下：

其中代表特征数或者是约束条件的数目，这里的是归一化的因子，因为需要满足所有的概率和为1，上式的未知数是,也就是说最大熵模型的解一定满足这个指数族的形式。这里直接给出结论了，详细推倒请看原始文章（点击这个可以下载，免费的） ：

上式的 Q就是指数族函数如下：

好，到这里我们找到了最大熵模型的解的结构，现在是如何确定参数 ，这里一般使用GIS算法（Generalized Iterative Scaling），这个算法思想和EM算法类似，如何解，下一节我们将详细讲解。