Python统计分析(2)——几种重要的概率分布：泊松分布

#泊松分布 (Poisson Distribution)

通俗定义：假定一个事件，在一段时间内随即发生，且概率符合以下条件： 1.将该时间段分割成若干个小的时间段，在这个接近于0的小时间段里，该事件发生一次的概率与该小时间段的长度成正比。 2.在每个极小时间段内，该事件连续发生两次以上的概率恒等于0. 3.该事件在不同的小时间段里，发生与否相互独立。

则该事件符合泊松分布。 泊松分布使用了以下符号： λ是事件发生的速率， t是时间间隔的长， X是该时间间隔内发生的事件数， 其中X是泊松随机变量，X的分布称为泊松分布， 令μ表示t时间间隔内平均发生的事件数，则μ=λ*t.

#泊松分布——绘图
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML

#PLOTTING CONFIG 绘图配置
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams['figure.figsize']=(14,7)
plt.figure(dpi=100)

#PDF 绘制泊松分布的概率密度函数
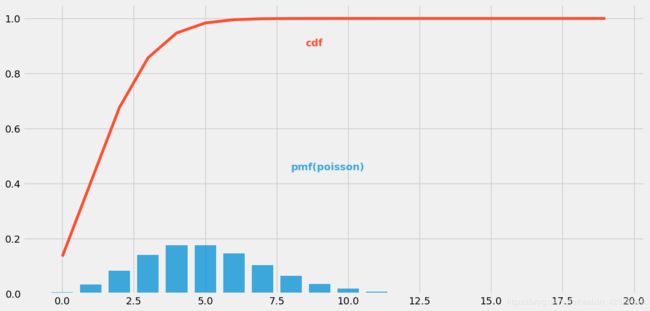
plt.bar(left=np.arange(20),height=(stats.poisson.pmf(np.arange(20),mu=5)),width=0.75,alpha=0.75)

#CDF 绘制泊松分布的累计概率曲线
plt.plot(np.arange(20),stats.poisson.cdf(np.arange(20),mu=2),color="#fc4f30")

#LEGEND 图例
plt.text(x=8,y=0.45,s="pmf(poisson)",alpha=0.75,weight="bold",color="#008fd5")
plt.text(x=8.5,y=0.9,s="cdf",rotation=.75,weight="bold",color="#fc4f30")

λ对结果的影响

plt.figure(dpi=100)
# PDF λ=1
plt.scatter(np.arange(20),stats.poisson.pmf(np.arange(20),mu=1),alpha=0.75,s=100)
plt.plot(np.arange(20),stats.poisson.pmf(np.arange(20),mu=1),alpha=0.75)

#PDF λ=5
plt.scatter(np.arange(20),stats.poisson.pmf(np.arange(20),mu=5),alpha=0.75,s=100)
plt.plot(np.arange(20),stats.poisson.pmf(np.arange(20),mu=5),alpha=0.75)

#PDF λ=10
plt.scatter(np.arange(20),stats.poisson.pmf(np.arange(20),mu=10),alpha=0.75,s=100)
plt.plot(np.arange(20),stats.poisson.pmf(np.arange(20),mu=10),alpha=0.75)

#LEGEND 图例
plt.text(x=3,y=0.1,s="$λ=1$",alpha=0.75,weight="bold",color="#008fd5")
plt.text(x=8.25,y=0.075,s="$λ=5$",rotation=.75,weight="bold",color="#fc4f30")
plt.text(x=14.5,y=0.06,s="$λ=10$",rotation=.75,weight="bold",color="#fc4f30")

在λ处，事件发生的次数的概率最大。

#绘制PDF
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize']=(14,7)

#绘制泊松分布的PMF曲线
x_s=np.arange(10)
y_s=stats.poisson.pmf(k=x_s,mu=5)
plt.scatter(x_s,y_s,s=100)

pmf值在μ处值最大。

#统计累积概率
#CDF
from scipy.stats import poisson

#求事件发生次数小于3的概率
print("p(x<3)={}".format(poisson.cdf(k=3,mu=5)))

#求事件发生次数大于2小于8的概率
print("p(2

p(x<3)=0.2650259152973616
p(2