基于贝叶斯准则的状态概率更新
\quad 基于贝叶斯准则表达获取测量值后的状态概率更新
\qquad 首先关于 Z = z Z=z Z=z的贝叶斯准则,只要 p ( y ∣ z ) > 0 p(y|z)>0 p(y∣z)>0:
p ( x ∣ y , z ) = p ( y ∣ x , z ) p ( x ∣ z ) p ( y ∣ z ) p(x|y,z)=\frac{p(y|x,z)p(x|z)}{p(y|z)} p(x∣y,z)=p(y∣z)p(y∣x,z)p(x∣z)
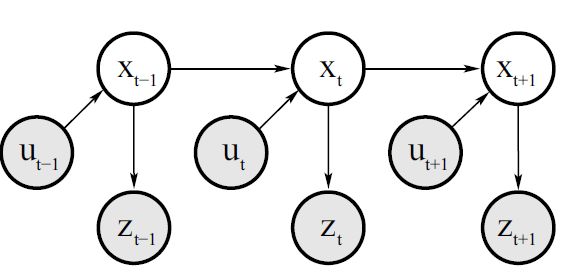
\qquad 由概率生成法则可得在获取测量值后状态概率的更新(目标后验)表达式
p ( x t ∣ z 1 : t , u 1 : t ) = p ( x t ∣ z t , z 1 : t − 1 , u 1 : t ) = p ( z t ∣ x t , z 1 : t − 1 , u 1 : t ) p ( x t ∣ z 1 : t − 1 , u 1 : t ) p ( z t ∣ z 1 : t − 1 , u 1 : t ) p(x_{t}|z_{1:t},u_{1:t})=p(x_{t}|z_{t},z_{1:t-1},u_{1:t})=\frac{p(z_{t}|x_{t},z_{1:t-1},u_{1:t})p(x_{t}|z_{1:t-1},u_{1:t})}{p(z_{t}|z_{1:t-1},u_{1:t})} p(xt∣z1:t,u1:t)=p(xt∣zt,z1:t−1,u1:t)=p(zt∣z1:t−1,u1:t)p(zt∣xt,z1:t−1,u1:t)p(xt∣z1:t−1,u1:t)此时 z 1 : t − 1 , u 1 : t z_{1:t-1},u_{1:t} z1:t−1,u1:t看作上式的条件 Z Z Z。
\qquad 依据伯努利分布(Bernoulli distribution)建模, θ g = 1 \theta_{g}=1 θg=1表示检测到目标,其概率使用 P i , k ( θ g = 1 ) P_{i,k}(\theta_{g}=1) Pi,k(θg=1)表示。 θ g = 0 \theta_{g}=0 θg=0表示未检测到目标,其概率使用 1 − P i , k ( θ g = 1 ) 1-P_{i,k}(\theta_{g}=1) 1−Pi,k(θg=1)表示。
\qquad 其中, i i i表示第 i i i个机器人, g g g表示概率密度栅格图中第 g g g个栅格, k k k表示第 k k k个时间点。使用符号 P i , g , k \mathcal{P}_{i,g,k} Pi,g,k定义概率 P i , k ( θ g = 1 ) P_{i,k}(\theta_{g}=1) Pi,k(θg=1)。则测量更新表达式为:
P i , g , k = P ( Z i , g , k ∣ θ g = 1 ) P i , g , k − 1 P ( Z i , g , k ∣ θ g = 1 ) P i , g , k − 1 + P ( Z i , g , k ∣ θ g = 0 ) ( 1 − P i , g , k − 1 ) \mathcal{P}_{i,g,k}=\frac{P(Z_{i,g,k}|\theta_{g}=1)\mathcal{P}_{i,g,k-1}}{P(Z_{i,g,k}|\theta_{g}=1)\mathcal{P}_{i,g,k-1}+P(Z_{i,g,k}|\theta_{g}=0)(1-\mathcal{P}_{i,g,k-1})} Pi,g,k=P(Zi,g,k∣θg=1)Pi,g,k−1+P(Zi,g,k∣θg=0)(1−Pi,g,k−1)P(Zi,g,k∣θg=1)Pi,g,k−1 \qquad 使用伯努利分布建模后的测量更新与一般式的不同表现在 归 一 化 常 数 η 使 用 测 量 概 率 的 全 概 率 公 式 表 示 \color{#F00}{归一化常数\eta使用测量概率的全概率公式表示} 归一化常数η使用测量概率的全概率公式表示。
\qquad 令 P ( Z i , g , k = 1 ∣ θ g = 1 ) = p , P ( Z i , g , k = 1 ∣ θ g = 0 ) = q P(Z_{i,g,k}=1|\theta_{g}=1)=p,P(Z_{i,g,k}=1|\theta_{g}=0)=q P(Zi,g,k=1∣θg=1)=p,P(Zi,g,k=1∣θg=0)=q,则
P i , g , k = { p P i , g , k − 1 p P i , g , k − 1 + q ( 1 − P i , g , k − 1 ) i f Z i , g , k = 1 , ( 1 − p ) P i , g , k − 1 ( 1 − p ) P i , g , k − 1 + ( 1 − q ) ( 1 − P i , g , k − 1 ) i f Z i , g , k = 0 , P i , g , k − 1 o t h e r w i s e . \mathcal{P}_{i,g,k}=\begin{cases} \frac{p\mathcal{P}_{i,g,k-1}}{p\mathcal{P}_{i,g,k-1}+q(1-\mathcal{P}_{i,g,k-1})}\quad if\ Z_{i,g,k}=1,\\ \frac{(1-p)\mathcal{P}_{i,g,k-1}}{(1-p)\mathcal{P}_{i,g,k-1}+(1-q)(1-\mathcal{P}_{i,g,k-1})}\quad if\ Z_{i,g,k}=0,\\ \mathcal{P}_{i,g,k-1}\quad otherwise. \end{cases} Pi,g,k=⎩⎪⎨⎪⎧pPi,g,k−1+q(1−Pi,g,k−1)pPi,g,k−1if Zi,g,k=1,(1−p)Pi,g,k−1+(1−q)(1−Pi,g,k−1)(1−p)Pi,g,k−1if Zi,g,k=0,Pi,g,k−1otherwise.化简得:
1 P i , g , k − 1 = { q p ( 1 P i , g , k − 1 − 1 ) , i f Z i , g , k = 1 1 − q 1 − p ( 1 P i , g , k − 1 − 1 ) , i f Z i , g , k = 0 1 P i , g , k − 1 − 1 , o t h e r w i s e . \frac{1}{\mathcal{P}_{i,g,k}}-1=\begin{cases} \frac{q}{p}(\frac{1}{\mathcal{P}_{i,g,k}-1}-1),\quad if\ Z_{i,g,k}=1\\ \frac{1-q}{1-p}(\frac{1}{\mathcal{P}_{i,g,k}-1}-1),\quad if\ Z_{i,g,k}=0\\ \frac{1}{\mathcal{P}_{i,g,k-1}}-1,\quad otherwise. \end{cases} Pi,g,k1−1=⎩⎪⎪⎨⎪⎪⎧pq(Pi,g,k−11−1),if Zi,g,k=11−p1−q(Pi,g,k−11−1),if Zi,g,k=0Pi,g,k−11−1,otherwise.对其取 l n ln ln运算,则
Q i , g , k = Δ l n ( 1 P i , g , k − 1 − 1 ) Q_{i,g,k}\overset{\Delta}{=}ln(\frac{1}{{P}_{i,g,k-1}}-1) Qi,g,k=Δln(Pi,g,k−11−1)则
Q i , g , k = Q i , g , k − 1 + v i , g , k Q_{i,g,k}=Q_{i,g,k-1}+v_{i,g,k} Qi,g,k=Qi,g,k−1+vi,g,k其中:
v i , g , k = Δ { l n q p , i f Z i , g , k = 1 l n 1 − q 1 − p , i f Z i , g , k = 0 0 , o t h e r w i s e . v_{i,g,k}\overset{\Delta}{=}\begin{cases} ln\frac{q}{p},\quad if\ Z_{i,g,k}=1\\ ln\frac{1-q}{1-p},\quad if\ Z_{i,g,k}=0\\ 0,\quad otherwise. \end{cases} vi,g,k=Δ⎩⎪⎨⎪⎧lnpq,if Zi,g,k=1ln1−p1−q,if Zi,g,k=00,otherwise. \qquad 由此,当目标存在时, Q i , g , k Q_{i,g,k} Qi,g,k趋向于 − ∞ -\infty −∞,即 P i , g , k \mathcal{P}_{i,g,k} Pi,g,k趋向于1。当目标不存在时, Q i , g , k Q_{i,g,k} Qi,g,k趋向于 + ∞ +\infty +∞,即 P i , g , k \mathcal{P}_{i,g,k} Pi,g,k趋向于0。
\qquad 其中潜在的问题是存储 Q i , g , k Q_{i,g,k} Qi,g,k过程中会出现数值过大,存储溢出的情况。给定边界 Q > 0 \boldsymbol{Q}>0 Q>0,使得
Q i , g , k = m a x { m i n ( Q i , g , k , Q ) , − Q } Q_{i,g,k}=max\{min(Q_{i,g,k},\boldsymbol{Q}),-\boldsymbol{Q}\} Qi,g,k=max{min(Qi,g,k,Q),−Q} \qquad 则 P i , g , k ∈ [ ( 1 / ( 1 + e Q ) ) , ( 1 / ( 1 + e − Q ) ] \mathcal{P}_{i,g,k}\in[(1/(1+e^{\boldsymbol{Q}})),(1/(1+e^{\boldsymbol{-Q}})] Pi,g,k∈[(1/(1+eQ)),(1/(1+e−Q)], Q \boldsymbol{Q} Q需要足够大使得 P i , g , k P_{i,g,k} Pi,g,k接近(0,1)。