交通咨询系统(最短路径问题)
【问题描述】
在交通网络非常发达、交通工具和交通方式不断更新的今天,人们在出差、旅游或做其他出行时,不仅关心节省交通费用,而且对里程和所需要的时间等问题也感兴趣。对于这样一个人们关心的问题,可用
一个图结构来表示交通网络系统,利用计算机建立一个交通咨询系统。图中的顶点表示城市,边表示城市之间的交通关系。这个交通系统可以回答出行旅客提出的各种路径选择问题。例如,问题之一:“一位旅
客要从 A 城到 B 城,他希望选择一条途中中转次数最少的路线。”假设图中每一站都需要换车,那么这个问题反映到图上就是要找一条从顶点 A 到顶点 B 的所含边数目最少的路径。我们只需要从顶点 A 出发对图
作广度优先搜索,一旦遇到顶点 B 就终止。由此所得广度优先生成树上,从根顶点 A 到顶点 B 的路径就是中转次数最少的路径。路径上 A 与 B 之间的顶点就是路径的中转站,但这只是一类最简单的图的最短路径问题。系统还可以回答诸如此类的等等的路径选择问题。设计一个交通咨询系统,为出差、旅游或做其他出行的客人提供各种路径选择信息查询服务。
【基本要求】
设计一个交通咨询系统,能让旅客咨询从任一个城市顶点到另一城市顶点之间的最短路径(里程)或最低花费或最少时间等问题。对于不同的咨询要求,可输入城市间的路程或所需时间或所需费用。
本设计共分三部分,一是建立交通网络图的存储结构;二是解决单源最短路径问题;三是实现任两个城市顶点之间的最短路径问题。
建立图的存储结构
图的邻接矩阵表示,除了需用一个二维数组存储顶点之间的相邻关系的邻接矩阵外,通常还需要使用一个具有 n 个元素的一维数组来存储顶点信息,其中下标为 i 的元素存储顶点 i 的信息。因此,图的邻接
矩阵的存储结构定义如下:
#define MVNum 50 //最大顶点数
typedef struct{
VertexType vexs[MVNum]; //顶点数组,类型假定为 char 型
Adjmatrix arcs[MVNum][MVNum]; //邻接矩阵,假定为 int 型
} MGraph; //图的邻接矩阵存储类型
单源最短路径
为了叙述方便,我们把路径上的开始点称为源点,路径的最后一个顶点为终点。
那么,如何求得给定有向图的单源最短路径呢?迪杰斯特拉(Dijkstra)提出按路径长度递增产生诸点的最短路径算法,称之为迪杰斯特拉算法。
任意一对顶点间最短路径
任意一对顶点间最短路径问题,是对于给定的有向网络图 G=(V,E),要对 G 中任意一对顶点有序对 “v,w(v !=w)”,找出 v 到 w 的最短路径。
要解决这个问题,我们可以依次把有向网络图中每个顶点作为源点,重复执行前面讨论的迪杰斯特拉算法 n 次,即可以求得每对顶点之间的最短路径。这里还可以用另外一种方法,称作费洛伊德(Floyd) 算法。
【测试实例】
测试实例一
图 5-1 是一个有向图,求顶点a到其余顶点的最短路径。
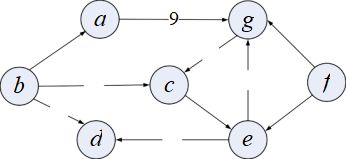
为了操作方便,对于图的顶点可以用序号来表示的,顶点的字母就用其对应的序号来表示,如a用 1来代替,„„。
运行实例二
图 5-2 是一个简单的交通网络图。求顶点“北京”到其余各城市之间的最短路径;并分别求“成都”到“上海”之间以及“上海”到“西安”之间的最短路径。为了操作方便,对于图的顶点可以用序号来表示的,顶点的字母就用其对应的序号来表示,如北京用1 来代替,„„。

#include<stdio.h>
#include<stdlib.h>
#define MVNum 50 //最大顶点数
#define Maxint 35000
enum boolean{FALSE,TRUE};
typedef char VertexType;
typedef int Adjmatrix;
typedef struct
{
VertexType vexs[MVNum]; //顶点数组,类型假定为char型
Adjmatrix arcs[MVNum][MVNum]; //邻接矩阵,假定为int型
}MGraph;
int D1[MVNum],p1[MVNum];
int D[MVNum][MVNum],p[MVNum][MVNum];
//采用邻接矩阵表示法构造有向图G
//n,e表示图的当前顶点数和边数
void CreateMGraph(MGraph *G,int n,int e)
{
int i,j,k,w;
for(i=1;i<=n;i++) //输入顶点信息
G->vexs[i]=(char)i;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
G->arcs[i][j]=Maxint; //初始化邻接矩阵
printf("输入%d条边的i,j及w:\n",e);
for(k=1;k<=e;k++)
{
//读入e条边,建立邻接矩阵
scanf("%d,%d,%d",&i,&j,&w);
G->arcs[i][j]=w;
}
printf("有向图的存储结构建立完毕! \n");
}
//dijkstra
//广度优先搜索
void Dijkstra(MGraph *G,int v1,int n)
{
//用Dijikstra算法求有向图G的v1顶点到其他顶点v的最短路径p[v]及其权D[v]
//S[v]为真当且仅当v属于s,及以求的从v1到v的最短路径
int D2[MVNum],p2[MVNum];
int v,i,w,min;
enum boolean S[MVNum];
for(v=1;v<=n;v++)
{
//初始化 S 和 D
S[v]=FALSE; //置空最短路径终点集
D2[v]=G->arcs[v1][v]; //置初始的最短路径值
if(D2[v]<Maxint)
p2[v]=v1; //v1是的前趋(双亲)
else
p2[v]=0; //v无前趋
}
D2[v1]=0; //S集初始时只有源点,源点到源点的距离为0
S[v1]=TRUE; //开始循环,每次求的V1到某个顶点的最短路径,并加V到S集中
for (i=2;i<n;i++)
{
//其余n-1个顶点
min=Maxint;
for(w=1;w<=n;w++)
if(!S[w]&&D2[w]<min)
{
//找离v1最近的顶点w,并将其赋给v,距离赋给min
v=w;
min=D2[w];
}
S[v]=TRUE;
for(w=1;w<=n;w++)
if(!S[w]&&(D2[v]+G->arcs[v][w]<D2[w]))
{
D2[w]=D2[v]+G->arcs[v][w];
p2[w]=v;
}
}
printf("路径长度 路径\n");
for(i=1;i<=n;i++)
{
printf("%5d",D2[i]);
printf("%5d",i);
v=p2[i];
while(v!=0)
{
printf("<-%d",v);
v=p2[v];
}
printf("\n");
}
}
//floyd(费洛伊德算法)
//使用n*n二维数组储存路径信息
//D[i][j]:记录每一对顶点的最短距离
void Floyd(MGraph *G, int n)
{
int i, j, k;
//储存每一对顶点之间的路径距离
for(i=1;i<=n;j++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(G->arcs[i][j]!=Maxint)
p[i][j]=j;
else
p[i][j]=0;
D[i][j]=G->arcs[i][j];
}
//k=1时只允许经过1号顶点进行中转
//k=2时只允许经过1号和2号顶点进行中转
//k=3......
//k=4......
for(k=1;k<=n;k++)
{
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
//如果顶点i到k,k到j的距离大于i直接到j距离则i到j的距离则需经过k顶点中转
if(D[i][k]+D[k][j]<D[i][j])
{
D[i][j]=D[i][k]+D[k][j];
p[i][j]=p[i][k];
}
}
}
}
//v:起点
//w:终点
int main()
{
MGraph *G;
int n,e,v,w,k;
int xz=1; //算法选择标志
G=(MGraph *)malloc(sizeof(MGraph)); //初始化图
printf("输入图中顶点个数和边数n,e:");
scanf("%d,%d",&n,&e);
CreateMGraph(G,n,e); //建立有向图结构
while(xz!=0)
{
printf(" 求城市之间的最短路径 \n");
printf("----------------------\n");
printf("1.求一个城市到所有城市的最短路径\n");
printf("2.求任意的两个城市之间的最短路径\n");
printf("-------------------\n");
printf("请选择:1 或 2, 选择 0:退出 ");
scanf("%d",&xz);
if(xz==2) //任意一对顶点间最短路径
{
Floyd(G,n);
printf("输入起点:");
scanf("%d",&v);
printf("输入终点:");
scanf("%d",&w);
k=p[v][w]; //k为v的后继结点
if(k==0)
{
printf("顶点%d 到 %d无路径!\n",v,w);
}else
{
printf("从顶点%d到%d的最短路径是:%d",v,w,v);
}
while(k!=w)
{
printf("-->%d",k);
k=p[k][w];
}
printf("--%d",w);
printf("路径长度:%d\n",D[v][w]);
}
if(xz==1)
{
printf("求单源路径,输入起点 v:");
scanf("%d",&v);
Dijkstra(G,v,n);
}
}
printf("结束求最短路径");
}
输入
1,2,2553
2,1,2553
1,3,695
3,1,695
1,4,704
4,1,704
2,3,511
3,2,511
2,5,812
5,2,812
3,4,349
4,3,349
3,6,1579
6,3,1579
4,7,651
7,4,651
5,6,2368
6,5,2368
6,7,1385
7,6,1385
有任何问题可以私聊