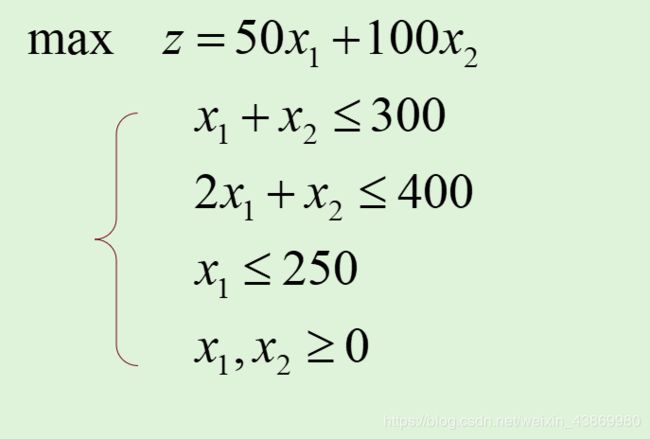使用单纯形法，scipy库和拉格朗日乘子法求解线性规划最大值和最优解问题

一、单纯形法

1.基本思想

单纯形法的基本思想是：先找出一个基本可行解，对它进行鉴别，看是否是最优解；若不是，则按照一定法则转换到另一改进的基本可行解,再鉴别；若仍不是，则再转换,按此重复进行。因基本可行解的个数有限，故经有限次转换必能得出问题的最优解。如果问题无最优解也可用此法判别。 根据单纯形法的原理，在线性规划问题中，决策变量（控制变量）x1，x2，…x n的值称为一个解,满足所有的约束条件的解称为可行解。使目标函数达到最大值（或最小值）的可行解称为最优解。这样，一个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值（或最小值）。求解线性规划问题的目的就是要找出最优解。

2.单纯形法的解题步骤

1）把线性规划问题的约束方程组表达成典范型方程组，找出基本可行解作为初始基本可行解。
2）若基本可行解不存在，即约束条件有矛盾，则问题无解。
3）若基本可行解存在，从初始基本可行解作为起点，根据最优性条件和可行性条件，引入非基变量取代某一基变量，找出目标函数值更优的另一基本可行解
4）按步骤3进行迭代,直到对应检验数满足最优性条件（这时目标函数值不能再改善），即得到问题的最优解。
5）若迭代过程中发现问题的目标函数值无界，则终止迭代。

二、求解例题

1、求解以下约束条件的线性规划的最大值和最优解

2.求解步骤

1）线性规范-标准化
以上题目的规范化如下所示：
引入松弛变量：s1,s2,s3

2）提取系数，填入表格
初始单纯性表的各个区域属性

区域解答结果：


s1,s2,s3作为基
3）求解
从初始基本可行解X0迭代出另一个基本可行解X1，并判断X1是否
为最优解。

总结一下步骤：
第一步，从原来的非基变量中选一个（称为进基变量）使其成为基本变量；
第二步，从原来的基本变量中选一个（称为离基变量）使其成为新的非基变量，最终求解即可得到结果。

3.求解结果验证

1）通过手工推导，上面的最优解为Z=27500
2）最优解为
X1=50
X2=250
S1=50
s2=s3=0

三、通过单纯形法求解线性规划最优解和最大值

1.新建txt文档，填入线性回归分析标准化模型

题目中的线性回归分析的标准化模型如下：

2.实现代码

1）导入需要的库

import numpy as np

2）定义列出线性回归系数模型函数

def pivot(d,bn):
    l = list(d[0][:-2])
    jnum = l.index(max(l)) #转入编号
    m = []
    for i in range(bn):
        if d[i][jnum] == 0:
            m.append(0.)
        else:
            m.append(d[i][-1]/d[i][jnum])
    inum = m.index(min([x for x in m[1:] if x!=0]))  #转出下标
    s[inum-1] = jnum
    r = d[inum][jnum]
    d[inum] /= r
    for i in [x for x in range(bn) if x !=inum]:
        r = d[i][jnum]
        d[i] -= r * d[inum]

2）定义更新基变量函数：从一个初始极点出发，不断找到更优的相邻极点，直到找到最优的极点（或极线）

def solve(d,bn):
    flag = True
    while flag:
        if max(list(d[0][:-1])) <= 0: #直至所有系数小于等于0
            flag = False
        else:
            pivot(d,bn)      

3）定义输出打印结果函数

def printSol(d,cn):
    for i in range(cn - 1):
        if i in s:
            print("x"+str(i)+"=%.2f" % d[s.index(i)+1][-1])
        else:
            print("x"+str(i)+"=0.00")
    print("objective is %.2f"%(-d[0][-1]))

4）导入线性回归模型、调用函数，求解最优解和最优值

d = np.loadtxt("回归分析标准化模型.txt", dtype=np.float)
(bn,cn) = d.shape
s = list(range(cn-bn,cn-1)) #基变量列表
solve(d,bn)
printSol(d,cn)

运行结果：

四、使用python中的scipy库对线性规划的最优解、最大值进行求解

1.线性回归模型

2.实现代码

#导入包
from scipy import optimize
import numpy as np
#确定c,A_ub,B_ub
c = np.array([50,100])
A_ub = np.array([[1,1],[2,1],[0,1]])
B_ub = np.array([300,400,250])
#求解
res =optimize.linprog(-c,A_ub,B_ub)
print(res)

运行结果：

五、通过拉格朗日乘子法进行该题求解

1.完整代码

#拉格朗日求解线性规划最大值和最优解
#导入sympy包，用于求导，方程组求解等等
from sympy import * 
#设置变量
x1 = symbols("x1")
x2 = symbols("x2")
alpha1 = symbols("alpha1")
alpha2 = symbols("alpha2")
alpha3 = symbols("alpha3")
#构造拉格朗日等式
L = 50 *x1-100*x2 + alpha1 * (x1+ x2-300) +alpha2 *(2*x1 + x2-400)
#求导，构造KKT条件
difyL_x1 = diff(L, x1)  #对变量x1求导
difyL_x2 = diff(L, x2)  #对变量x2求导
difyL_alpha2 = diff(L, alpha2)  #对乘子alpha2求导
dualCpt =alpha1 * (x1+ x2-300)
#求解KKT等式
aa = solve([difyL_x1, difyL_x2, dualCpt,difyL_alpha2], [x1, x2,alpha1,alpha2])
#打印结果，还需验证kkt约束条件
for i in aa:
    if i[2] >= 0 and i[0]>=0 and i[1]>=0:
        if (i[0]+i[1]-300) <= 0 and (2*i[0]+i[1]-400) <= 0 and (i[0]-250)<=0:
            print(i)

2.运行结果

六、单纯形法和scipy库求解结果对比

单纯形法：

scipy库：

对比一看，scipy库方法的结果精确到小数点后好几位，但单纯形法就是很完美的整数，更贴近例题而且两者的误差很小。