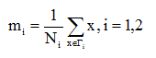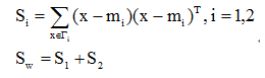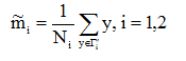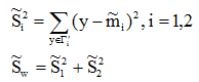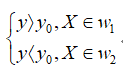Fisher线性判别器 python实现 实验报告
实验目的
为了进一步理解和掌握Fisher线性判别法的基本原理和实现过程，利用Fisher判别法解决实际问题进行试验。
实验环境
Windows 10，Python 3.7.4，PyCharm 2019.2.3
实验原理
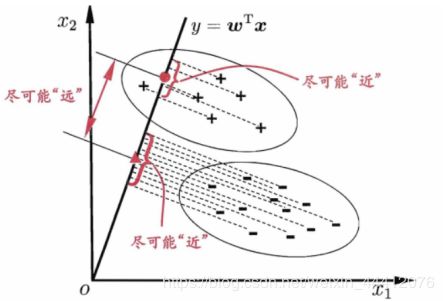
Fisher线性判别法的基本思想是：通过寻找一个投影方向（线性变换，线性组合），将高维问题降低到一维空间来解决，并且要求变换后的一维数据类间离散度尽可能大，类内离散度尽可能小，能够使得两类之间尽可能分开，各类的内部又能尽可能聚集，如图1-1。
Fisher线性判别分析，就是通过给定的训练数据，确定投影方向W和阈值y0，即确定线性判别函数，然后根据这个线性判别函数，对测试数据进行测试，得到测试数据的类别。
基本参数：
1.在d维空间
（1）各类样本均值向量
（2）样本的类内离散度矩阵，总的类内离散度矩阵
（3）样本间类内离散度
2.在一维空间
（1）各类样本的均值
（2）样本类内离散度 和总样本类内离散度
通过以上Fisher线性判别法思想的分析，可以得到Fisher准则函数：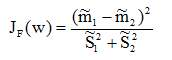
我们所要求解的是最优的投影方向W*，但准则函数中并没有跟W的相关项，所以需要利用上面的基本参数代入化解，得到一个利用上面参数所表示的准则函数并且包含W的相关项，从而得到：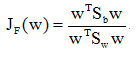
下面是需要求解出能使的W*。由于上式符合使用拉格朗日乘子法的形式，利用Lagrange乘子法，计算得出：
得到的只是最优的投影方向，但不能确定分类面的具体位置，因此要一个阈值。在本次实验中采用的是基于先验概率的求解方式，即
对于某一个未知类别的样本向量X，如果
实验内容
实验介绍
已知有两类数据和二者的先验概率，已知P(w1)=0.6，P(w2)=0.4。
w1中数据点的坐标对应一一如下：
x1 = 0.23, 1.52, 0.65, 0.77, 1.05, 1.19,
0.29, 0.25, 0.66, 0.56, 0.90, 0.13,
-0.54, 0.94, -0.21, 0.05, -0.08, 0.73,
0.33, 1.06, -0.02, 0.11, 0.31, 0.66
y1 = 2.34, 2.19, 1.67, 1.63, 1.78, 2.01,
2.06, 2.12, 2.47, 1.51, 1.96, 1.83,
1.87, 2.29, 1.77, 2.39, 1.56, 1.93,
2.20, 2.45, 1.75, 1.69, 2.48, 1.72
W2中数据点的坐标对应一一如下：
x2 = 1.40, 1.23, 2.08, 1.16, 1.37, 1.18,
1.76, 1.97, 2.41, 2.58, 2.84, 1.95,
1.25, 1.28, 1.26, 2.01, 2.18, 1.79,
1.33, 1.15, 1.70, 1.59, 2.93, 1.46
y2 = 1.02, 0.96, 0.91, 1.49, 0.82, 0.93,
1.14, 1.06, 0.81, 1.28, 1.46, 1.43,
0.71, 1.29, 1.37, 0.93, 1.22, 1.18,
0.87, 0.55, 0.51, 0.99, 0.91, 0.71
（1）利用上面数据确定并画出Fisher准则下的最优投影方向，给出分类阈值。
（2）根据所得结果判断（1,1.5），（1.2,1.0），（2.0,0.9），（1.2,1.5），（0.23，2.33）,属于哪个类别，并画出数据分类相对应的结果图，要求画出其在W上的投影。
实验流程图
实验步骤
（1）导入数据
（2）将矩阵整合为w1,w2的类型
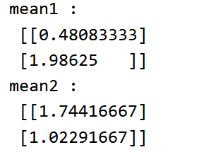
（3）计算两类的均值向量
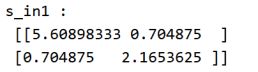
（4）计算总的类内离散度矩阵
（5）计算投影方向和阈值
（6）对测试数据进行分类判别
（7）显示分类结果
（8）计算实验点在w_new方向上的投影
（9）绘图显示
实验结果
运行效果图如6-1所示，在图中红色的“+”号是属于第一类w1类的样本点，绿色的“▉”是属于第二类w2的样本点，黑色的“★”是属于第一类w1类的测试样本点，蓝色的“◇”是第二类w2的测试样本点，直线是找到的最优投影方向，在线上的点是测试点在投影方向的投影点。
实验小结
通过这次实验我对Fisher线性判别法有了进一步的更加直观的理解，我所做的实验比较简单，但能够找到Fisher线性判别的最佳投影方向和阈值，能利用所建立的分类器进行未知点的类别的预测。在实验过程中，自己的编码水平有待提高，在代码中仍然存在一些小问题，比如浪费内存资源的问题，可以进一步改进。
代码资源
请到主页资源处查找。