Animated Exploration of Dynamic Graphs with Radial Layout

论文：《Animated Exploration of Dynamic Graphs with Radial Layout》

---

Abstract:

    本文使用径向树布局方法，通过焦点的交互选择来动画变换新布局。为了使转换易于遵循，动画线性插值节点的极坐标，同时强制排序和方向约束。 我们将此技术应用于社交网络和Gnutella文件共享网络的可视化，并讨论我们的非正式可用性测试的结果。

1.Introduction:

    在本文中，通过选择单个节点作为感兴趣的中心或焦点来确定图的视图。这项工作的主要贡献是一种新技术，即用于以平滑，吸引人的方式动画从一个视图到下一个视图的过渡。该算法通过线性插值节点的极坐标并对新布局实施约束来增强众所周知的径向布局方法[7,8,12]，以使其尽可能与先前的布局相似。

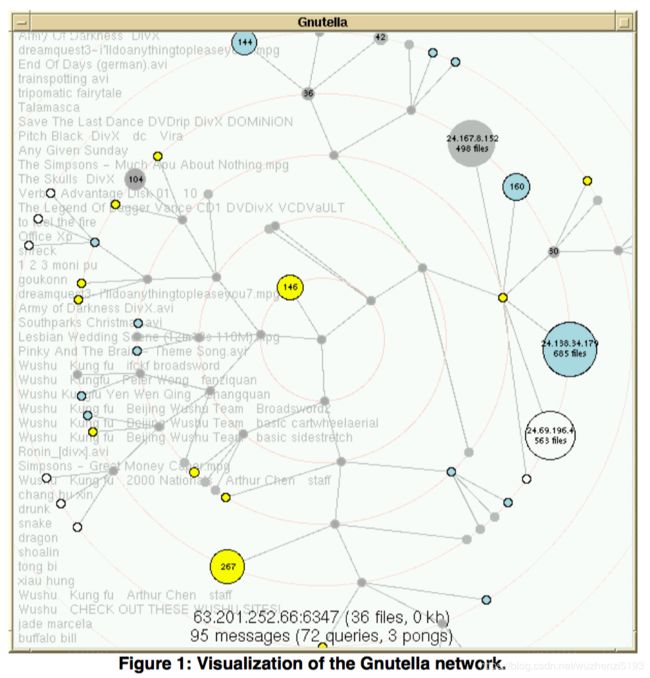
    当结合远离焦点的聚合或消除节点的方法时，我们的技术也可以提供探索非常大的图的有效方法。图1显示了我们实施的实施，应用于Gnutella网络的可视化[11]。

2.Method:

   我们假设给出了一个由一个连通组件组成的图。 随着时间的推移，图形可以随着节点的插入或删除而动态地改变。 我们将图中边缘连接的任意两个节点称为“邻居”。在此可视化方法中，查看者可以通过选择任何可见节点作为焦点节点。 然后以该点为焦点重新排列网络

2.1 Layout Technique

    我们将图形视为以焦点节点为根的树。 我们通过从焦点开始执行图的广度优先遍历来确定树中的父子关系。 除焦点之外的每个节点都将有一个邻居作为其父节点，可能还有一些其他邻居作为其子节点，并且可能还有其他非“非树”邻居。

    布局后，绘制线条以显示图形中的所有边，非树边以不同于树中边的颜色绘制。

  2.1.1 Radial Layout

    由于关注的焦点是单个节点，因此将该焦点节点放置在显示器的中心并围绕它布置其他节点是很自然的。这里使用了一种简单的布局“径向绘图”。节点布置在焦点节点周围的同心环上。每个节点位于环上，对应于距焦点的最短网络距离。焦点的直接邻居位于最小的内环上，它们的邻居位于第二个最小的环上，依此类推。我们的实现明确地绘制了这些环以使网络距离明显。

    节点在其环上的角位置由分配给它的环的扇区确定。每个节点在分配给其父节点的扇区内被分配一个扇区，其大小与该节点的子树的角宽度成比例。类似于此的方法在[22]中被详细描述为“径向放置”，其中所有节点具有相同的大小，因此节点的子树的角宽度仅仅是其后代中的叶节点的数量。

  2.1.2 Space Allocation

    我们的算法允许以不同的大小绘制节点。为了最大限度地减少较大节点阻塞较小节点的可能性，我们在环上分配空间时考虑每个节点的大小。每个单独节点的角宽度是其直径除以其距焦点的距离。我们可以为每个节点计算这个，因为我们知道从每个节点到焦点的网络距离。我们通过计算其顶部节点的角宽度，子子树的总角度宽度以及选择这两个量中较大的一个来找到任何子树的宽度。每个节点位于分配给它的角度扇区的中心。

    图2说明了两个示例图的布局方法。在这两种情况下，节点A都是焦点，并且它被分配全部360度以在其子节点之间分配。节点B有许多自己的子节点，因此它给它的角度空间比它的兄弟节点更多。分配给节点B的子树的区域被轻微着色。节点B的孩子躺在第二个环上;节点C（这些子节点之一）被分配以较暗阴影显示的第二个环的切片。然后将所有节点C的后代排列在该阴影区域内。

    我们的算法可以轻松地适应节点的添加和删除。径向布局是动态变化图形的合理选择，因为节点的添加或删除仅扰乱其兄弟节点，特别是当图形变得密集时。

2.2 Animation Technique

    为了探索图形，用户选择可见节点以成为新焦点。通过从新焦点执行广度优先搜索来找到新布局树，从而计算从新焦点到每个节点的网络距离。节点之间的边被重新解释为一组新的父子关系。如上所述，通过将每个节点分配给适当的环并分配环的角度扇区来确定新布局。

    虽然这足以从新焦点的角度显示图形，但简单地切换到这个新视图可能会导致高度迷惑的重新排列。为了减少这种迷失方向，我们使用动画来执行平滑过渡，并对新布局强制执行一些约束以使其与当前布局类似，以便更容易遵循过渡。

    动画已经有效地用于其他工作，以帮助维护数据可视化和用户界面中的方向。信息可视化器[2,14,18]中的锥形树和透视墙使用三维动画来帮助用户跟踪对象。当用户改变焦点时，Eades和Huang在力导图中使用动画来平滑过渡[9]。

    一些其他交互式图形浏览器还保留不变量以帮助保持用户定向。例如，在H3中，当选择节点时，动画过渡将其移动到球体的中心。过渡包括一个旋转分量，这样当节点到达中心时，它的祖先在它的左边，而它的后代出现在右边[16]。

    Hyperbolic浏览器[13]将节点和链接放在双曲线空间内;改变焦点节点实际上改变了空间的哪个部分当前居中。相比之下，在我们的系统中，改变焦点节点通常会改变节点相对于彼此的布局。这在双曲线浏览器中不是必需的，因为它仅应用于树结构，而我们的方法旨在显示具有相关交叉线的图形。

  2.2.1 Transition Paths

    布局之间最简单的过渡将沿着直线路径将每个节点从其旧位置移动到新位置。 然而，这种线性插值会产生混乱的动画。 在大多数过渡中，许多节点停留在同一个环上或移动到相邻的环，但是直线移动可能导致节点离开其环并在返回之前远离它。 直线运动还会导致许多节点聚集在显示器中心的不可读的丛中，然后在它们接近最终位置时分离。

    由于节点是径向定位的，因此线性插值节点的极坐标而不是它们的直角坐标更有意义。因此，停留在环上的节点跟随环的圆周，而环变化的节点平滑地从一个环螺旋到另一个环。当兄弟子树维持它们的顺序时，这也保留了在整个过渡期间分配给兄弟子树的区域之间的边界，使得向中心移动的节点不会与正在出路的其他节点发生冲突。

    径向布局算法产生一种隐含的期望，即径向距离应始终传达距离焦点的网络距离;在极坐标空间中插值与此期望一致。结果是一个更平滑的动画，其中节点组围绕图形的中心一起旋转。以这种方式聚类节点大大减少了理解动画的认知努力，因为它允许人类视觉系统将组成对象组合成一个单元。它还使节点以弧形而不是直线移动，借用传统动画中的有效技术[3]。

  2.2.2 Transition Constraints

    我们设计了两个约束来维持旧布局和新布局之间的最佳一致性。

    首先，我们选择新布局的方向，以减少旋转行程。考虑所选新焦点的当前父节点。这个父母必须在第一个环上结束，因为它是新焦点的直接邻居。我们确定新布局的方向，以便连接新焦点及其父级的边的方向保持不变。图4显示了选择节点A成为新焦点的示例。节点A的当前父节点是节点B;新布局的方向使得边缘AB保持相同的方向。

    其次，因为图形不一定是树，所以节点的一些新子节点当前可能是它的非邻居。当节点将角色从邻居变为直接子节点时，这可能导致边缘交叉。为了避免这个问题，我们检查当前布局中每个边到节点邻居的方向，从连接节点到新父节点的边缘开始，顺时针进行。然后，我们在新布局中维护这种儿童的顺序。

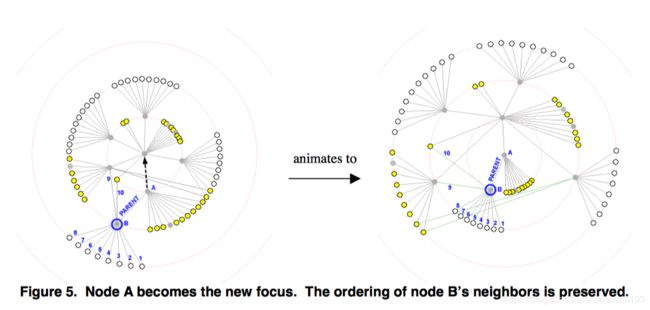
    这确保了在过渡期间新布局中的树边缘不会彼此重合。在图5中，当前驻留在环1上的节点A被选择成为新焦点。考虑在此转换期间节点B（节点A的子节点）会发生什么。在转换之前，边1到8是节点B的子节点的边，边9和10是非树边。在转换期间，节点B前往环1，而其邻居（节点A除外）全部前往环2.注意边1到10如何保持它们的相对顺序。这确保了在过渡期间新布局中的树边缘不会彼此重合。

  2.2.3 Animation Timing

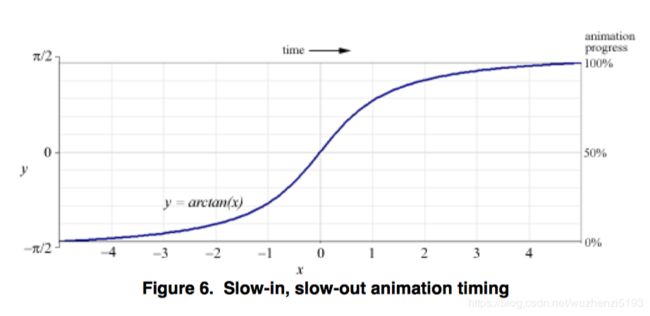
    最后，我们希望在动画的开头和结尾提供最佳的视觉恒定性。 将另一种传统动画技术应用于交互[3]，我们使用慢速，慢速时序而不是直线时序。 如图6所示，这是通过使用一部分反正切函数来控制动画随时间推移的进度来实现的。 动画开始缓慢，平稳加速，然后在结束时减速。 大多数运动发生在时间间隔的中间三分之一。 这提供了良好的视觉提示，以帮助用户预测节点移动到新位置。

  2.2.4 Scalability

    这种技术似乎适用于数百个节点。 对于较大的图形，直接从中心节点跳到外围节点可能会迷失方向。 在这种情况下，沿着图中从旧焦点节点到新焦点节点的路径执行一系列到中间焦点节点的转换可能更好。 通过明智地聚合或隐藏显示器中的外围节点，还可以使该技术更好地扩展。

5.Conslusions

    我们设计，实现并测试了以焦点加上下文风格交互式探索图形的技术。 我们提出了一种新方法，用于以一种吸引人的方式动画从一个视图到下一个视图的过渡，从而减少混淆。 我们结合了极坐标空间中的插值技术，慢入，慢速运动时序以及对布局的约束的强制执行，以产生平滑且易于遵循的过渡。

    我们成功地将这些技术应用于社交网络和Gnutella文件共享网络的可视化。 非正式用户测试支持我们的假设，即动画，使用极坐标进行插值，节点上的排序约束以及慢进，慢速时序都可以提高在探索图形时维护上下文的能力。 这项工作的一个自然延伸是将这种技术与聚合或消除节点的方法相结合[22]，以便探索非常大的图形。