(SRCNN)及pytorch实现_Learning a Deep Convolutional Network for Image Super-Resolution——超分辨率(二)
文章目录
- Learning a Deep Convolutional Network for Image Super-Resolution
- 算法简介
- 算法流程
- Patch extraction and representation
- Non-linear mapping 非线性映射
- Reconstruction
- 训练
- 测试
- 实验结果
Learning a Deep Convolutional Network for Image Super-Resolution
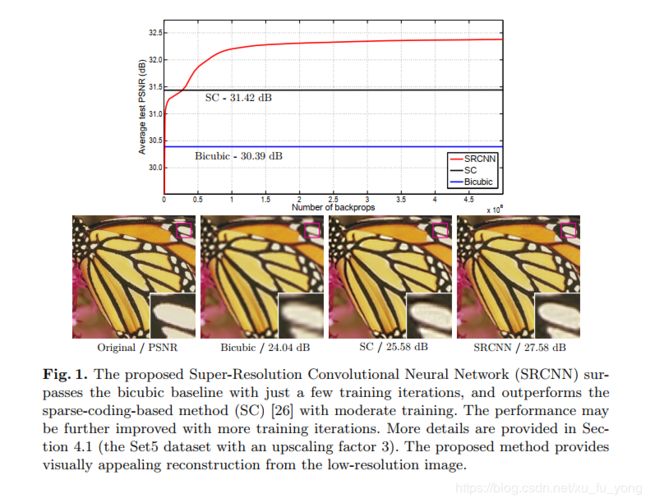
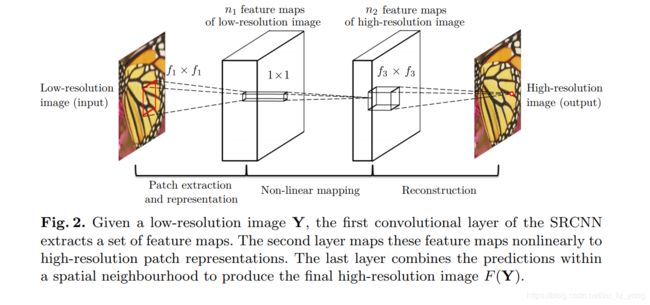
SRCNN是深度学习用在超分辨率重建上的开山之作。SRCNN的网络结构非常简单,仅仅用了三个卷积层,网络结构如下图所示。
论文链接: (Learning a Deep Convolutional Network for Image Super-Resolution, ECCV2014)
Pytorch实现源码
算法简介
SRCNN算法的框架,SRCNN将深度学习与传统稀疏编码之间的关系作为依据,将3层网络划分为图像块提取(Patch extraction and representation)、非线性映射(Non-linear mapping)以及最终的重建(Reconstruction)。
SRCNN的流程为:
(1)先将低分辨率图像使用双三次差值放大至目标尺寸(如放大至2倍、3倍、4倍),此时仍然称放大至目标尺寸后的图像为低分辨率图像(Low-resolution image),即图中的输入(input);
(2)将低分辨率图像输入三层卷积神经网络,(举例:在论文中的其中一实验相关设置,对YCrCb颜色空间中的Y通道进行重建,网络形式为(conv1+relu1)—(conv2+relu2)—(conv3))第一层卷积:卷积核尺寸9×9(f1×f1),卷积核数目64(n1),输出64张特征图;第二层卷积:卷积核尺寸1×1(f2×f2),卷积核数目32(n2),输出32张特征图;第三层卷积:卷积核尺寸5×5(f3×f3),卷积核数目1(n3),输出1张特征图即为最终重建高分辨率图像。
们首先使用双三次插值将其放大到所需的大小,这是我们执行的唯一预处理3。让我们将插值图像表示为Y.我们的目标是从Y中恢复与地面实况高分辨率图像X尽可能相似的图像F(Y)。为了便于呈现,我们仍称Y为“低分辨率的“图像,虽然它与X具有相同的大小。我们希望学习映射F,它在概念上由三个操作组成:
- 1)补丁提取和表示:该操作从低分辨率图像Y中提取(重叠)补丁,并将每个补丁表示为高维向量。这些向量包括一组特征图,其数量等于向量的维数。
- 2)非线性映射:该操作是每个高维向量到另一个高维向量的非线性映射。每个映射的矢量在概念上是高分辨率补丁的表示。这些向量包括另一组特征映射。
- 3)重建:该操作聚合高分辨率补丁表示以生成最终的高分辨率图像。该图像应该与真实标记X相似。
算法流程
Patch extraction and representation
图像恢复中的流行策略是密集地提取补丁,然后通过一组预先训练的基础(例如PCA,DCT,Haar等)来表示它们。这相当于用一组滤波器对图像进行卷积,每个滤波器都是一组基。将这些基础的优化包括在网络的优化中。第一层表示为操作 F 1 F_{1} F1:
F 1 ( Y ) = max ( 0 , W 1 ∗ Y + B 1 ) F_{1}(\mathbf{Y})=\max \left(0, W_{1} * \mathbf{Y}+B_{1}\right) F1(Y)=max(0,W1∗Y+B1)
其中 W 1 W_{1} W1和 B 1 B_{1} B1分别代表滤波器和偏置。这里 W 1 W_{1} W1的大小为 c × f 1 × f 1 × n 1 c \times f_{1} \times f_{1} \times n_{1} c×f1×f1×n1,其中c是输入图像中的通道数, f 1 f_{1} f1是滤波器的空间大小, n 1 n_{1} n1是滤波器的数量。很明显, W 1 W_{1} W1在图像上应用 n 1 n_{1} n1个卷积,每个卷积的内核大小为 c × f 1 × f 1 c \times f_{1} \times f_{1} c×f1×f1。输出由 n 1 n_{1} n1个特征图组成。 B 1 B_{1} B1是 n 1 n_{1} n1维向量,其每个元素与滤波器相关联。我们在滤波器响应上应用整流线性单元(ReLU,max(0,x))
Non-linear mapping 非线性映射
第一层为每个补丁提取 n 1 n_{1} n1维特征。在第二操作中,我们将这些 n 1 n_{1} n1维向量中的每一个映射为 n 2 n_{2} n2维向量。这相当于应用具有平凡空间支持1 x 1的 n 2 n_{2} n2滤波器。此解释仅适用于1 x 1过滤器。但是很容易推广到像3 x 3或5 x 5这样的大型滤波器 。在那种情况下,非线性映射不是输入图像的补丁; 相反,它是在3 x 3或5 x 5特征图的“补丁”。第二层的操作是:
F 2 ( Y ) = max ( 0 , W 2 ∗ F 1 ( Y ) + B 2 ) F_{2}(\mathbf{Y})=\max \left(0, W_{2} * F_{1}(\mathbf{Y})+B_{2}\right) F2(Y)=max(0,W2∗F1(Y)+B2)
这里 W 2 W_{2} W2的大小是 n 1 × 1 × 1 × n 2 n_{1} \times 1 \times 1 \times n_{2} n1×1×1×n2, B 2 B_{2} B2是 n 2 n_{2} n2维。每个输出 n 2 n_{2} n2维向量在概念上是将用于重建的高分辨率补丁的表示。
Reconstruction
在传统方法中,经常对预测的重叠高分辨率补丁进行平均以产生最终的完整图像。平均可以被认为是一组特征图上的预定义滤波器(其中每个位置是高分辨率补片的“扁平”矢量形式)。由此推动,我们定义卷积层以产生最终的高分辨率图像:
F ( Y ) = W 3 ∗ F 2 ( Y ) + B 3 F(\mathbf{Y})=W_{3} * F_{2}(\mathbf{Y})+B_{3} F(Y)=W3∗F2(Y)+B3
这里 W 3 W_{3} W3的大小是 n 2 × f 3 × f 3 × c n_{2} \times f_{3} \times f_{3} \times c n2×f3×f3×c, B 3 B_{3} B3是三维矢量。
训练
(1)训练数据集:论文中某一实验采用91张自然图像作为训练数据集,对训练集中的图像先使用双三次差值缩小到低分辨率尺寸,再将其放大到目标放大尺寸,最后切割成诸多33×33图像块作为训练数据,作为标签数据的则为图像中心的21×21图像块(与卷积层细节设置相关);
(2)损失函数:采用MSE函数作为卷积神经网络损失函数;
L ( Θ ) = 1 n ∑ i = 1 n ∥ F ( Y i ; Θ ) − X i ∥ 2 L(\Theta)=\frac{1}{n} \sum_{i=1}^{n}\left\|F\left(\mathbf{Y}_{i} ; \Theta\right)-\mathbf{X}_{i}\right\|^{2} L(Θ)=n1i=1∑n∥F(Yi;Θ)−Xi∥2
(3)卷积层细节设置:第一层卷积核9×9,得到特征图尺寸为(33-9)/1+1=25,第二层卷积核1×1,得到特征图尺寸不变,第三层卷积核5×5,得到特征图尺寸为(25-5)/1+1=21。训练时得到的尺寸为21×21,因此图像中心的21×21图像块作为标签数据。(卷积训练时不进行padding)
测试
(1)全卷积网络:所用网络为全卷积网络,因此作为实际测试时,直接输入完整图像即可;
(2)Padding:训练时得到的实际上是除去四周(33-21)/2=6像素外的图像,若直接采用训练时的设置(无padding),得到的图像最后会减少四周各6像素(如插值放大后输入512×512,输出500×500)。因此在测试时每一层卷积都进行了padding(卷积核尺寸为1×1的不需要进行padding)。这样保证插值放大后输入与输出尺寸的一致性。