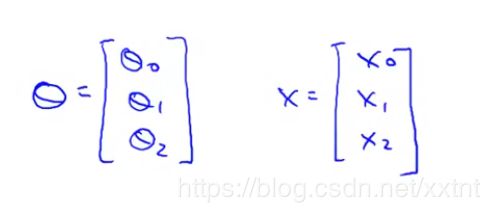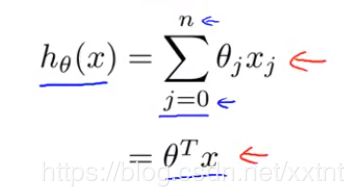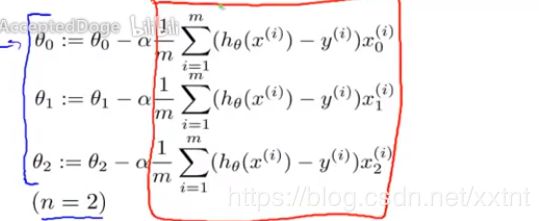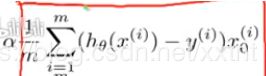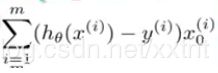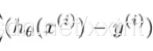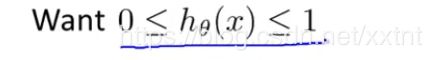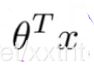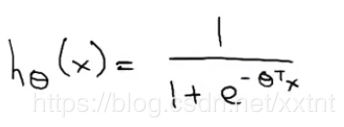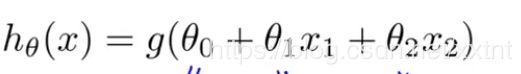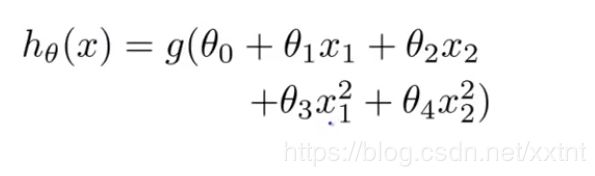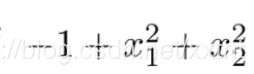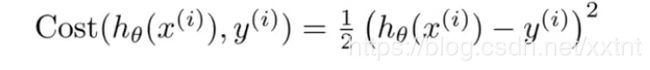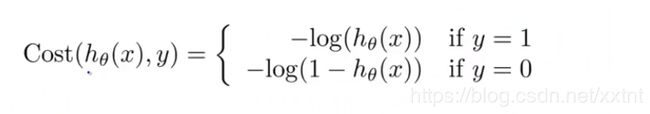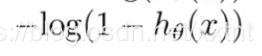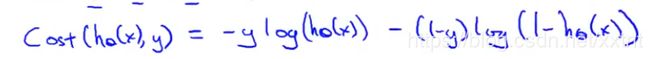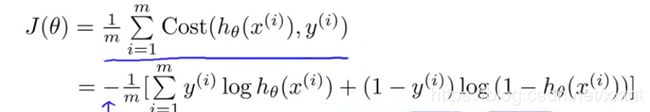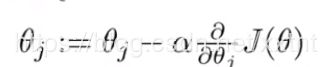吴恩达机器学习——逻辑回归和分类算法

 

高效使用软件

如下所示，是一个函数，这是一个求theta和x的积的和的公式，这个问题我们可以轻松地通过矩阵的方式解决。

 

将theta和x以如下形式表示，theta和x的矩阵的积就是这个函数的结果。

 

求解theta的值

 

进行逻辑分解：

Theta(i) = theta(i) – aβ

β =

 

然后进行进一步分解：

这个部分可以看做是两个矩阵的积： 和 矩阵的积

依次这样慢慢划分，就能够实现这个theta的求解。

 

 

 

分类算法

 

Y = {0,1}

0表示负类，负类表示缺少某种东西

1表示正类，正类表示永远某种东西

 

我们现在只研究划分成两个类的问题（即二元分类问题）

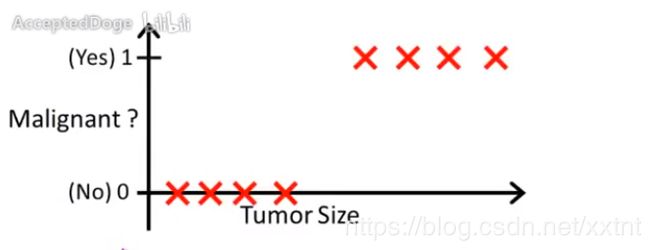
这是一个简单的例子，肿瘤大小与是否为良性的关系，我们可以进行简单的分类

如上所示，x表示肿瘤的大小，x经过h运算后大于0.5的是恶性肿瘤，这个是一个比较简单的划分。

 

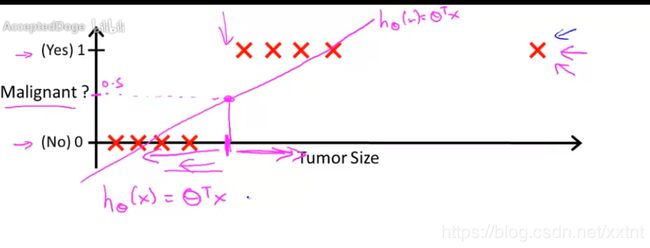
接下来，进行一下小小的扩展：

 

如果在右边很远处，有一个恶性肿瘤，如果安装原来的想法，我们不能正确的划分最右边的那个肿瘤为恶性肿瘤，因此线性回归可能不太适用于这个数据集。因为适用线性回归满足上式的线性回归会让绝大部分的肿瘤都输入恶性肿瘤，而不满足实际生活。

 

 

 

逻辑回归

解决用什么样的函数进行分类的问题

首先我们规定，目标函数的值的范围在0和1之间，我们目标函数的值来表示概率

 

 

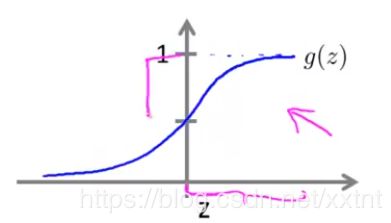
我们约定g(z) = 1/(1+e^(-Z))

这个g(z)它永远满足其值为（0,1）之间

令z =

联立上面几个式子，可以得到：

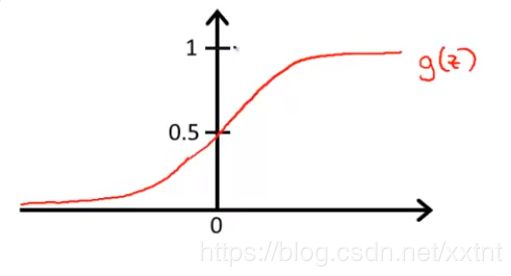
大概绘制函数图像如下（基本满足实际肿瘤分类）：

首先我们简单梳理一下：

P(肿瘤是良性的)=p(0)

P(肿瘤是恶性的)=p(1)

P(0)+p(1)=1根据概率可知

而h(x)则是得恶性肿瘤的概率

因此h(x) = 1-p(0)

 

我们规定当g(z)≥0.5时为恶性肿瘤，而当g(z)＜0.5时为良性肿瘤

同时，我们让：θ的转置*X=Z（θ即参数）

因此Z>0就是：θ的转置*X>0

同时，由于函数g特殊性，当z>0时，g(z)>0.5,当z小于0时，g(z)小于0.5。因此我们可以通过判断z的值，即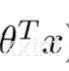 的值来进行分类。

 

 

假设这是我们的一个训练集，这是它的逻辑回归函数

假如我们已经算出了各个θ的值，具体如何计算出θ的值，将在后续课程进行讲解。

 

在这个实例中，当 >0,则该样本划分为1，当 <0时，该样本划分为0；

在这个实例中，θ0 = -3 ； θ1 = 1 ； θ2 = 1；

因此化简后：-3+x1+x2≥0时，样本属于1，反之，则属于0。

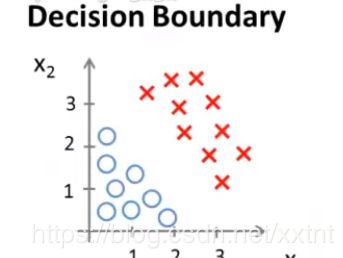
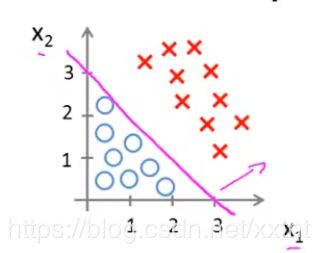
通过这个式子，我们得到一条直线（如下图）

直线左边的样本都属于0，直线右边的样本都属于1，这条直线被称为决策边界

 

 

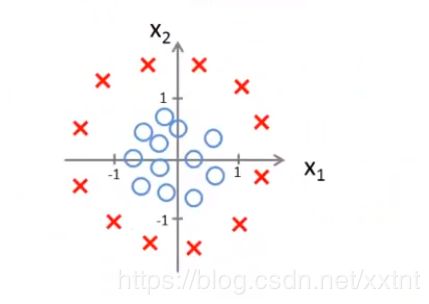
实例2

假设我们设定的函数如下

根据 ：

θ0 = -1

θ1 = 0

θ2 = 0

θ3 = 1

θ4 = 1

我们可以设置 θ = [ -1 0 0 1 1]

同时，我们将x1和x2两个变量带入化简得到关系式如下：

如果这个关系式大于0则该样本属于1，反之则属于0

 

通过训练集计算参数θ的值

首先，我们需要设定一个新的关于θ的代价函数

 

按照原来的思路，我们得到的代价函数如下：

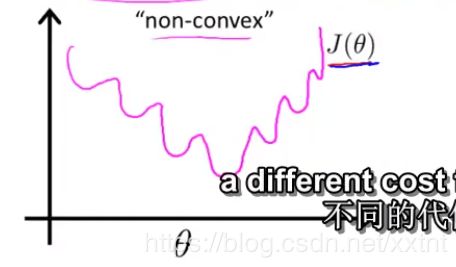
如上图，由于hθ(x)函数测特殊性，会导致代价函数画出来的图形为一个非凸图形（如下）

因此，首先我们要用不同的代价函数，让代价函数的他图形不为一个非凸图形，尽可能表现为下图所示：

 

 

 

我们画出的代价函数和逻辑回归函数的关系如上图

这个代价函数的性质：

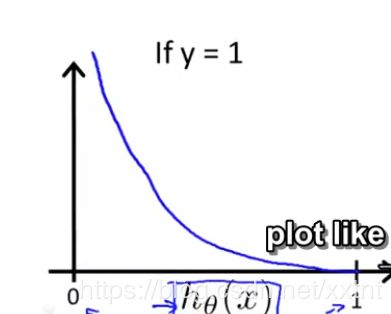
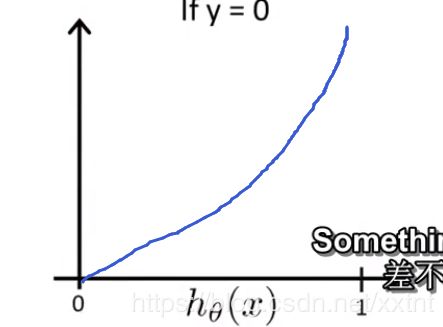
1、当h(x) = 1时，y = 1, 代价函数的值为0

2、当h(x)趋近于0时，代价函数趋近于无穷大

解释为尽管h(x)已经非常接近于0了，肿瘤为恶性肿瘤的可能性为0，但是肿瘤确实为恶性肿瘤。

 

 

如果y = 0,则h(x)≤0.5，则代价函数的值为

代价函数和逻辑回归函数的值的关系如上图

 

我们为了避免代价函数有两个，所以我们需要用一个方法将代价函数合并成一个

 

 

我们根据y只为0或1的前提，通过将y带入这个式子，来形成一个新的代价函数，其效果等同于上面的关系式

因此代价函数如下：

 

在这个式子中，我们要找到一个θ，满足上式，使代价函数的值尽可能最小

通过梯度下降的基本公式

 

我们求出偏导数，然后得到求θ的式子如下：

 

 

 

 

 

 

 

 

 

 

 

 

 

：