C#图与图的算法之深度优先遍历

关于图与图的算法，应该这样去学习：

1.应该从图的概念讲起，例如无向图和有向图等，明白图是什么，能够表示哪些实际问题。

2.学习图应该用怎样的数据结构去表示，这里就会学到邻接矩阵法和邻接链表法等数据结构，比较两种数据结构的优劣，在后面的算法学习中会用到。

3.学习图的基础算法：基础的同样是最重要的，包括：深度优先遍历，广度优先遍历和拓扑排序等。

4.学习图的一些高级算法（后面会陆续介绍）。

这里简单介绍一下深度优先遍历。

1.什么是深度优先的遍历？

举个例子：你有4个瓜ABCD，每个瓜之间都有藤蔓缠着，你打算顺着这个藤怎么去摸瓜？例如，现在有A瓜在手里，A和BC都连接着，B和CD也连接着，如果是广度优先，那么找完A接着就会去找与其相连的B和C，如果是深度优先，那么找完A就会找B，然后接着找B下面的C和D，然后接着找C（或者D）下面的瓜。

所以深度优先就是沿着纵深的角度，只要有新的没有找过的点，我就去把它找出来，想到这里你是否已经联想到，这就类似二叉树的递归遍历，只要子树还有节点没有访问，那么就先访问子树节点。那么，其实广度优先遍历就像二叉树遍历中的层序遍历，依次输出该节点的所有子节点。

如果还不太明白，请看代码，这里有详细的注释：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using static System.Console;

namespace 图的遍历__深度优先遍历
{
    //这里图的数据结构采用邻接链表法
    class Node
    {
        //每一个顶点的表示
        public int x;
        public Node next;
        public Node(int x)
        {
            this.x = x;
            this.next = null;
        }
    }
    class GraphLink
    {
        //每一个邻接链表的表示
        //就是一个简单的单链表
        public Node first;
        public Node last;
        public bool Isempty()
        {
            return first == null;
        }
        public void Print()
        {
            Node current = first;
            while (current != null)
            {
                Write("[" + current.x + "]");
                current = current.next;
            }
        }
        public void Insert(int x)
        {
            //在当前链表中插入节点
            Node newnode = new Node(x);
            if (this.Isempty())
            {
                first = newnode;
                last = newnode;
            }
            else
            {
                last.next = newnode;
                last = newnode;
            }
        }
    }
    class Program
    {
        public static int[] run = new int[9];
        public static GraphLink[] head = new GraphLink[9];
        public static void DFS(int current)
        {
            ///
            ///深度优先遍历(DFS)的算法
            ///
            //run是每个节点的数组，1~8，用1表示该节点已经访问过
            run[current] = 1;
            Write("[" + current + "]");
            while ((head[current].first) != null)
            {
                //如果该节点所指的下一个节点未被访问，那么就递归访问该节点
                if (run[head[current].first.x] == 0)
                {
                    DFS(head[current].first.x);
                }
                //进行到这里说明深度已经到底了，开始往回找了
                head[current].first = head[current].first.next;
            }
        }
        static void Main(string[] args)
        {
            //1~8这八个节点之间的联系关系
            int[,] Data = { { 1, 2 }, { 2, 1 }, { 1, 3 }, { 3, 1 }, { 2,4},
                                        { 4,2},{ 2,5},{ 5,2},{ 3,6},{ 6,3},
                                        { 3,7},{ 7,3},{ 4,5},{ 5,4},{ 6,7},
                                        {7,6},{ 5,8},{ 8,5},{ 6,8},{ 8,6} };
            int i, j;
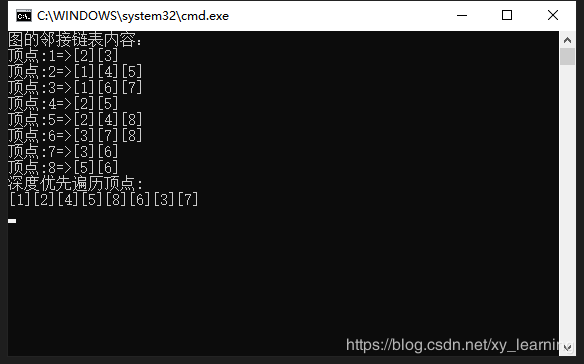
            WriteLine("图的邻接链表内容：");
            for (i = 1; i < 9; i++)
            {
                //每个顶点初始化为0，表示未访问过
                run[i] = 0;
                head[i] = new GraphLink();
                Write("顶点:" + i + "=>");
                for (j = 0; j < 20; j++)
                {
                    if (Data[j, 0] == i)
                    {
                        head[i].Insert(Data[j, 1]);
                    }
                }
                head[i].Print();
                WriteLine();
            }
            WriteLine("深度优先遍历顶点:");
            DFS(1);
            WriteLine();
            ReadKey();
        }
    }
}

对照看输出结果：