快速线性筛法求素数
说到求素数,其实在刚开始学C++的时候就已经见过诸如此类的问题,不过现在最常见的还是筛法求素数
谈及筛法求素数,其大致思路可分为如下五步:
(1).把2到n的自然数放入a[2]到a[n]中(所放入的数与下标号相同) ;
(2).在数组元素中以下标为序,按顺序找到未曾找过的最小素数minp和它的位置p(即下标号);
(3).从p+1开始,把凡是能被minp整除的各元素值从a数组中划去(筛掉),也就是把该元素标记为0;
(4).让p=p+1,重复执行第(2) (3)步骤,知道,minp>floor(sqrt(n))为止;
(5).打印输出a数组中留下来的数,未被筛掉的各元素值;
这种求素数的算法很容易被理解,其时间复杂度介于O(n)~O(n*logn)是一种比较流行的方法。但是同样的,这种算法也存在先天性的缺陷,我们简单分析:
对于一个数30,可分解为30=2*15=3*10=5*6,显然,当循环,2,3,5,6,10,15时都会筛除一次30这个数,而
当n很大时,就会出现许多的冗余操作,这个算法可以进一步进行优化来使算法的效率提高,因此,一种名为
快速线性筛法的算法应运而生。这种算法的智慧之处在于——对于2~n的每一个数,它只筛去到目前为止它能
筛到而之后的其他数筛不到的几个合数,而把它能筛到,另有别的数也能筛到的数留个接下来的数去筛,这
样的话就能使得素数的筛选不重不漏——说起来容易做起来难,这样的算法应该如何实现呢?
对于快速筛法求素数,其步骤也可分为如下几个阶段:
(1).开一个n+1大小的数组num[n]来存放每一个元素的筛留情况(即对于num[n]的每个数与下标号相同,对于任
意num[n]有num[n]=0,num[n]=1两种情况,如果num[n]=0则是素数,反之num[n]=1时是合数);
(2).再开一个数组prime[n]来存放筛出的素数以便最后输出结果;
(3).对于一个数k,总是进行从n*prime[0]~n*prime[j](由小到大来乘),直到if(n%prime[j]==0)成立时break掉
这是这个算法的精髓所在,所以弄清楚原因是十分必要的!!!
对于一个数c=a*b(b为c的最小质因数),当通过该算法的循环循环至c*b时,易得此时c%b==0,如果此时继续循环至b后面的一个素数d,则有:c*d=a*b*d=(a*d)*b,因为d>b,所以a*d>c。当循环从c继续查找到a*d时我们发现当a*d再次与素数b想乘时,就又对c*d进行了一次操作,出现了冗余,所以在if(n%prime[j]==0)成立时要将该层循环break掉;
举个例子,对于一个数9,9*2=18将18标记为合数,循环继续;9*3=27将27标记为合数,此时发现9%3=0,循环退出。如果将循环继续下去会出现筛除9*5=45的情况,而45=15*3,在15时会被在筛去一次,故不可行
(4)完成了算法中最重要的一步,最后只要将存放筛出的prime[ ]数组中的素数即可!
这种算法的写法也十分简单,这里只给出一种与普通筛法求素数比较程序,如下:
#include
#include
#include
#include
#define inf 20000005
using namespace std;
int n;
bool a[inf+1];
long num[inf+1]={1,1},prime[inf+1]={0},number=0; //number 记录素数个数
void putongshaifa() //普通筛法求素数
{
clock_t begin,end;
begin=clock();
for(int i=0;i<=n;++i)
a[i]=true;
a[1]=false;
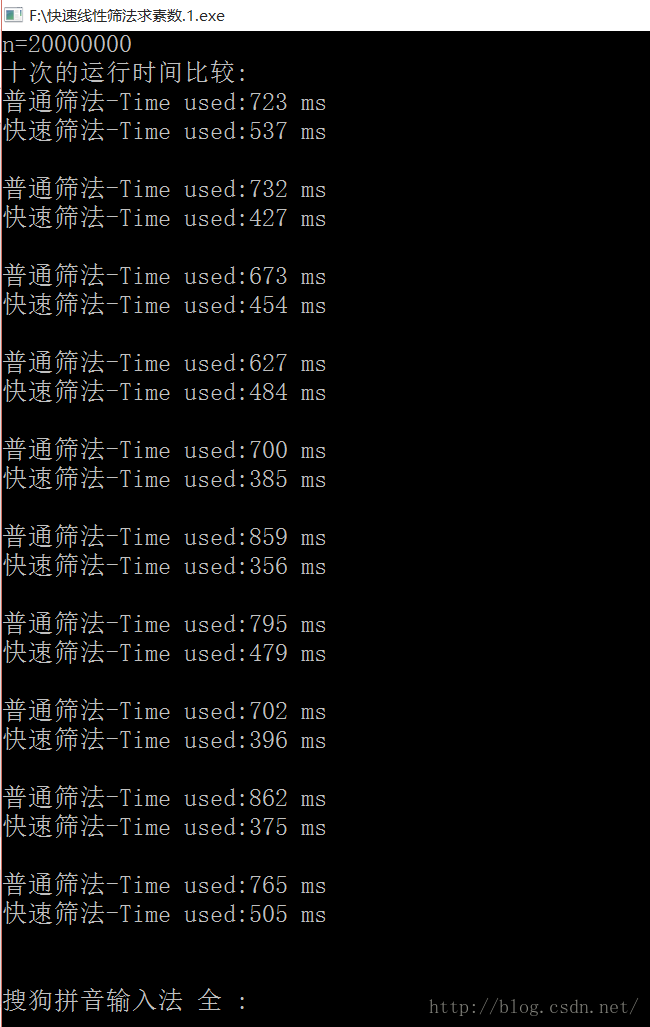
for(int i=2;i 通过比较,两种算法的差异一目了然:
由上述数据不难看出,快速线性筛法的效率基本比普通筛法求素数的效率高一倍,说明这的确是一种比较可
靠的关于求素数优化的算法~!