树状数组

树状数组详解（转）

第01讲 什么是树状数组？

树状数组用来求区间元素和，求一次区间元素和的时间效率为O(logn)。

有些同学会觉得很奇怪。用一个数组S[i]保存序列A[]的前i个元素和，那么求区间i,j的元素和不就为S[j]-S[i-1]，那么时间效率为O(1)，岂不是更快？

但是，如果题目的A[]会改变呢？例如：

我们来定义下列问题：我们有n个盒子。可能的操作为

1.向盒子k添加石块

2.查询从盒子i到盒子j总的石块数

自然的解法带有对操作1为O(1)而对操作2为O(n)的时间复杂度。但是用树状数组，对操作1和2的时间复杂度都为O(logn)。

第02讲 图解树状数组C[]

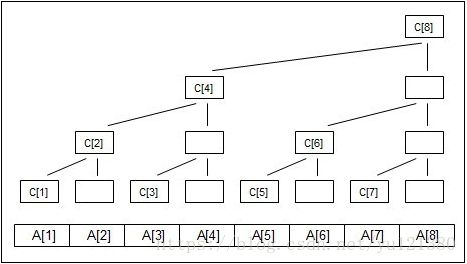
现在来说明下树状数组是什么东西？假设序列为A[1]~A[8]

 

 

网络上面都有这个图，但是我将这个图做了2点改进。

（1）图中有一棵满二叉树，满二叉树的每一个结点对应A[]中的一个元素。

（2）C[i]为A[i]对应的那一列的最高的节点。

现在告诉你：序列C[]就是树状数组。

那么C[]如何求得？

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]= A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

以上只是枚举了所有的情况，那么推广到一般情况，得到一个C[i]的抽象定义：

因为A[]中的每个元素对应满二叉树的每个叶子，所以我们干脆把A[]中的每个元素当成叶子，那么：C[i]=C[i]的所有叶子的和。

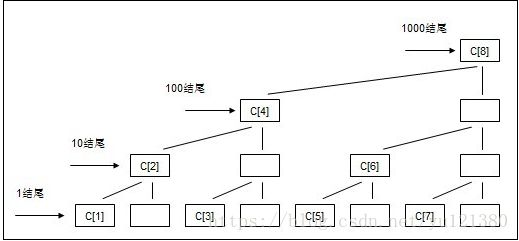
现在不得不引出关于二进制的一个规律：

先仔细看下图：

将十进制化成二进制，然后观察这些二进制数最右边1的位置：

1 --> 00000001

2 --> 00000010

3 --> 00000011

4 --> 00000100

5 --> 00000101

6 --> 00000110

7 --> 00000111

8 --> 00001000

1的位置其实从我画的满二叉树中就可以看出来。但是这与C[]有什么关系呢？

接下来的这部分内容很重要：

在满二叉树中，

以1结尾的那些结点（C[1],C[3],C[5],C[7]），其叶子数有1个，所以这些结点C[i]代表区间范围为1的元素和；

以10结尾的那些结点（C[2],C[6]），其叶子数为2个，所以这些结点C[i]代表区间范围为2的元素和；

以100结尾的那些结点（C[4]），其叶子数为4个，所以这些结点C[i]代表区间范围为4的元素和；

以1000结尾的那些结点（C[8]），其叶子数为8个，所以这些结点C[i]代表区间范围为8的元素和。

扩展到一般情况：

i的二进制中的从右往左数有连续的x个“0”，那么拥有2^x个叶子，为序列A[]中的第i-2^x+1到第i个元素的和。

终于，我们得到了一个C[i]的具体定义：

C[i]=A[i-2^x+1]+…+A[i]，其中x为i的二进制中的从右往左数有连续“0”的个数。

第03讲 利用树状数组求前i个元素的和S[i]

理解了C[i]后，前i个元素的和S[i]就很容易实现。

从C[i]的定义出发：

C[i]=A[i-2^x+1]+…+A[i]，其中x为i的二进制中的从右往左数有连续“0”的个数。

我们可以知道：C[i]是肯定包括A[i]的，那么：

S[i]=C[i]+C[i-2^x]+…

也许上面这个公式太抽象了，因为有省略号，我们拿一个具体的实例来看：

S[7]=C[7]+C[6]+C[4]

因为C[7]=A[7]，C[6]=A[6]+A[5]，C[4]=A[4]+A[3]+A[2]+A[1]，所以S[7]=C[7]+C[6]+C[4]

（1）i=7，求得x=0，那么我们求得了A[7]；

（2）i=i-2^x=6，求得x=1，那么求得了A[6]+A[5]；

（3）i=i-2^x=4，求得x=2，那么求得了A[4]+A[3]+A[2]+A[1]。

讲到这里其实有点难度，因为S[i]的求法，如果要讲清楚，那么得写太多的东西了。所以不理解的同学，再反复多看几遍。

从（1）（2）（3）这3步可以知道，求S[i]就是一个累加的过程，如果将2^x求出来了，那么这个过程用C++实现就没什么难度。

现在直接告诉你结论：2^x=i&(-i)

证明：设A’为A的二进制反码，i的二进制表示成A1B，其中A不管，B为全0序列。那么-i=A’0B’+1。由于B为全0序列，那么B’就是全1序列，所以-i=A’1B，所以：

i&(-i)= A1B& A’1B=1B，即2^x的值。

1、主要理解了“x+=lowbit(x)” 和 “x-=lowbit(x)” 和 “x--”这个理解了是在做什么即可，直接看图。

“x+=lowbit(x)”：访问直系父结点，比如：C[1]点开始，则会访问：C[1] --> C[2] --> C[4] --> C[8]。

“x-=lowbit(x)”：访问同一辈的左兄弟结点，比如：C[7]点开始，则会访问：C[7] --> C[6] --> C[4] --> End。

所以根据（1）（2）（3）的过程我们可以写出如下的函数：

int Sum(int i) //返回前i个元素和

{

       int s=0;

       while(i>0)

       {

              s+=C[i];

              i-=i&(-i);

       }

       return s;

}

第04讲 更新C[]

正如第01讲提到的小石块问题，如果数组A[i]被更新了怎么办？那么如何改动C[]？

如果改动C[]也需要O(n)的时间复杂度，那么树状数组就没有任何优势。所以树状数组在改动C[]上面的时间效率为O(logn)，为什么呢？

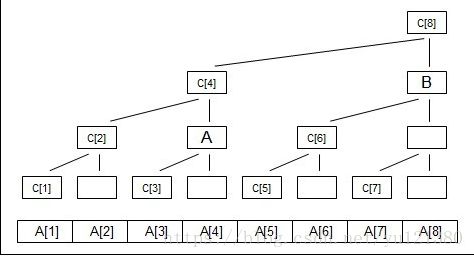
因为改动A[i]只需要改动部分的C[]。这一点从第02讲的图中就可以看出来：

如上图：

假如A[3]=3，接着A[3]+=1，那么哪些C[]需要改变呢？

答案从图中就可以得出：C[3],C[4],C[8]。因为这些值和A[3]是有联系的，他们用树的关系描述就是：C[3],C[4],C[8]是A[3]的祖先。

那么怎么知道那些C[]需要变化呢？

我们来看“A”这个结点。这个“A”结点非常的重要，因为他体现了一个关系：A的叶子数为C[3]的2倍。因为“A”的左子树和右子树的叶子数是相同的。 因为2^x代表的就是叶子数，所以C[3]的父亲是A，A的父亲是C[i+2^0]，即C[3]改变，那么C[3+2^0]也改变。

我们再来看看“B”这个结点。B结点的叶子数为2倍的C[6]的叶子数。所以B和C[6+2^1]在同一列，所以C[6]改变，C[6+2^1]也改变。

推广到一般情况就是：

如果A[i]发生改变，那么C[i]发生改变，C[i]的父亲C[i+2^x]也发生改变。

这一行的迭代过程，我们可以写出当A[i]发生改变时，C[]的更新函数为：

void Update(int i,int value)  //A[i]的改变值为value

{

       while(i<=n)

       {

              C[i]+=value;

              i+=i&(-i);

       }

}

第05讲 一维树状数组的应用举例

废了4讲的话，我们终于把一维树状数组的2个不到5行的代码给搞定了。现在要正式投入到应用当中。

题目链接：http://poj.org/problem?id=2352

题意：按照y升序给你n个星星的坐标，如果有m个星星的x,y坐标均小于等于星星A的坐标，那么星星A的等级为m。

分析：是一道树状数组题。举例来说，以下是题目的输入：

5

1 1

5 1

7 1

3 3

5 5

由于y坐标是升序的且坐标不重复，所以在星星A后面输入的星星的x,y坐标不可能都小于等于星星A。假如当前输入的星星为（3,3），易得我们只需要去找 树状数组中小于等于3的值就可以了，即GetSum(3)。注意：A[i]表示x坐标为i的个数，C[]为A[]的树状数组，那么GetSum(i)就是 序列中前i个元素的和，即x小于等于i的星星数。

本题还是一点要注意：星星坐标的输入可以是（0,0），所以我们把x坐标统一加1，然后用树状数组实现。

第06讲 二维树状数组

BIT可用为二维数据结果。假设你有一个带有点的平面(有非负的坐标)。你有三个问题：

1.在(x , y)设置点

2.从(x , y)移除点

3.在矩形(0 , 0), (x , y)计算点数 - 其中(0 , 0)为左下角，(x , y)为右上角，而边是平行于x轴和y轴。

对于1操作，在（x,y）处设置点，即Update(x,y,1)，那么这个Update要怎么写？很简单，因为x，y坐标是离散的，所以我们分别对x,y进行更新即可，函数如下：

void Update(int x,int y,int val)

{

       while(x<=n)

       {

              int y1=y;

              while(y1<=n)

              {

                     C[x][y1]+=val;

                     y1+=y1&(-y1);

              }

              x+=x&(-x);

       }

}

那么根据Update可以推得：GetSum函数为：

int GetSum(int x,int y)

{

       int sum=0;

       while(x>0)

       {

              int y1=y;

              while(y1>0)

              {

                     sum+=C[x][y1];

                     y1-=y1&(-y1);

              }

              x-=x&(-x);

       }

       return sum;

}

第07讲 二维树状数组的应用举例

题目链接：http://poj.org/problem?id=2155

我们先讨论POJ2155的一维情况，如下：

有一个n卡片的阵列。每个卡片倒放在桌面上。你有两个问题：

  1. T i j (反转从索引i到索引j的卡片，包括第i张和第j张卡——面朝下的卡将朝上；面朝上的卡将朝下)

  2. Q i (如果第i张卡面朝下回答0否则回答1)

解决：

解决问题(1和2)的方法有时间复杂度O(log n)。在数组f(长度n + 1)我们存储每个问题T(i, j)——我们设置f[i]++和f[j + 1]--。对在i和j之间(包括i和j)每个卡k求和f[1] + f[2] + ... + f[k]将递增1，其他全部和前面的一样(看图2.0清楚一些)，我们的结果将描述为和(和累积频率一样)模2。

图 2.0

使用BIT来存储(增加/减少)频率并读取累积频率。

理解了一维的情况，POJ2155就是其二维的版本，易得只需要更(x1,y1)，(x1,y2+1)，(x2+1,y1)，(x2+1,y2+1)四个点的C[]的值就可以了，最后的结果依然是GetSum(x,y)%2

keep moving...

 

hdu1556

解题思路

 

这道题可以用很多方法来做，线段树是最容易想到的，但是代码实现上很复杂

其实这道题可以把每次染色的点抽象为每次涂改的区间，然后对要查询的点所在区间的更新次数进行求和

这样就可以在时间上，大大缩短，查询和统计的时间复杂度都为log(n)

树状数组中的每个节点都代表了一段线段区间，每次更新的时候，根据树状数组的特性可以把b以前包含的所有区间都找出来，然后把b以前的区间全部加一次染色次数。然后，再把a以前的区间全部减一次染色次数，这样就修改了树状数组中的[a,b]的区间染色次数，查询每一个点总的染色次数的时候，就可以直接向上统计每个父节点的值，就是包含这个点的所有区间被染色次数，这就是树状数组中向下查询，向上统计的典型应用

Ps:根据个人理解层次的不同，这道题也可以向上查询，向下统计，还可以向下查询，向下统计，不过我写的这种是最容易理解的

 

代码实现如下：

用cin,cout进行读写操作的话，会超时，所以我还是用的scanf()，printf()

​
#include   
#include   
const int MAXN=110000;  
int n,c[MAXN];  
int lowbit(int x)  
//计算2^k  
{  
    x=x&-x;  
    return x;  
}  
void update(int num,int val)  
//向下查询，num是要更新的子节点，val是要修改的值  
{  
    while(num>0)  
    {  
        c[num]+=val;  
        num-=lowbit(num);  
    }  
}  
int getSum(int num)  
//向上统计每个区间被染色的次数  
{  
    int sum=0;  
    while(num<=n)  
    {  
        sum+=c[num];  
        num+=lowbit(num);  
    }  
    return sum;  
}  
int main()  
{  
    int a,b;  
    while(scanf("%d",&n),n)  
    {  
        memset(c,0,sizeof(c));  
        for(int i=0;i

二维树状数组

我在前面已经介绍过了树状数组的各种操作，但是你会轻易的发现前面我们介绍的树状数组都是一维的，那既然一维可以，那么会不会有二维的树状数组呢？ 
答案是肯定的。 
那么我今天就来教大家如何实现二维的树状数组。 
今天我介绍基本的功能：

1. 对二维数组内某一点加上一个值
2. 求一原点为一个端点的子矩阵和
3. 求以二维数组中的两个点为端点的子矩阵和

我们先来讲讲怎么去表示。（分析字太多了，以下的分析采用南宫逸辰的分析） 
数组A[][]的树状数组定义为：

C[x][y] = ∑ a[i][j], 其中， 
x-lowbit(x) + 1 <= i <= x, 
y-lowbit(y) + 1 <= j <= y.

例：举个例子来看看C[][]的组成。 
设原始二维数组为： 
　A[][]={{a11,a12,a13,a14,a15,a16,a17,a18,a19}, 
{a21,a22,a23,a24,a25,a26,a27,a28,a29}, 
{a31,a32,a33,a34,a35,a36,a37,a38,a39}， 
{a41,a42,a43,a44,a45,a46,a47,a48,a49}}; 
那么它对应的二维树状数组C[][]呢？

记: 
B[1]={a11,a11+a12,a13,a11+a12+a13+a14,a15,a15+a16,…} 这是第一行的一维树状数组 
B[2]={a21,a21+a22,a23,a21+a22+a23+a24,a25,a25+a26,…} 这是第二行的一维树状数组 
B[3]={a31,a31+a32,a33,a31+a32+a33+a34,a35,a35+a36,…} 这是第三行的一维树状数组 
B[4]={a41,a41+a42,a43,a41+a42+a43+a44,a45,a45+a46,…} 这是第四行的一维树状数组 
那么： 
C[1][1]=a11,C[1][2]=a11+a12,C[1][3]=a13,C[1][4]=a11+a12+a13+a14,c[1][5]=a15,C[1][6]=a15+a16,… 
这是A[][]第一行的一维树状数组

C[2][1]=a11+a21,C[2][2]=a11+a12+a21+a22,C[2][3]=a13+a23,C[2][4]=a11+a12+a13+a14+a21+a22+a23+a24, 
C[2][5]=a15+a25,C[2][6]=a15+a16+a25+a26,… 
这是A[][]数组第一行与第二行相加后的树状数组

C[3][1]=a31,C[3][2]=a31+a32,C[3][3]=a33,C[3][4]=a31+a32+a33+a34,C[3][5]=a35,C[3][6]=a35+a36,… 
这是A[][]第三行的一维树状数组

C[4][1]=a11+a21+a31+a41,C[4][2]=a11+a12+a21+a22+a31+a32+a41+a42,C[4][3]=a13+a23+a33+a43,… 
这是A[][]数组第一行+第二行+第三行+第四行后的树状数组

好，南宫逸辰分析结束。 
我简单总结一下，说白了，就是：

每一行都是一个树状数组， 
以行为元素，整个列也是一个树状数组。

（这句话请记住，这个思想会贯穿始终） 
既然如此，我相信代码也很快就出来了，接下来我就来给出代码，并进行简单的解释。

单点修改

void add(int x,int y,int v)
{
	int yy=y;
	while(x<=n)
	{
		y=yy;
		while(y<=m)
		{
			c[x][y]+=v;
			y+=lowbit(y);
		}
		x+=lowbit(x);
	}
}

这个根据我刚刚说的两个树状数组（那句贯穿始终的话），就很容易理解了。 
我们外围循环枚举每一行，内循环在行内进行一维树状数组的单点修改，从而实现二维树状数组的单点修改。

以原点为一个端点的子矩阵和

ll getsum(int x,int y)
{
	ll sum=0;
	int yy=y;
	while(x>0)
	{
		y=yy;
		while(y>0)
		{
			sum+=c[x][y];
			//printf("%lld****\n",sum);
			y-=lowbit(y);
		}
		x-=lowbit(x);
	}
	return sum;
}

还是那句贯穿始终的话，外围枚举行，内围则是一维树状数组前几项和。这样就能完成我们的任务了。

以任意两点为左上和右下两个端点的子矩阵和

ll Sum(int x1,int y1,int x2,int y2)
{
	return getsum(x2,y2)+getsum(x1-1,y1-1)-getsum(x2,y1-1)-getsum(x1-1,y2);
}

和以为树状数组一样，我们依然借助sum去求。 
但是，我们看到，这个公式似乎很长，别急，别晕，听我解释一边即可明白。 
首先声明，我们保证x2>=x1,y2>=y1 
下面让我们先来看一个图： 
 
红色的矩形是我们要求的。 
我们这里为了和计算机里二维数组的保持一致，我们把x坐标视为纵坐标。（感谢qie_wei指正我的错误） 
首先sum(x2,y2)很显然是整个大矩形， 
sum(x1-1,y2)和sum(x2,y1-1)则是绿色和黄色的两个矩阵（不含红色边），很明显这是我们不要的，所以我们用大的矩阵减去这两个小矩阵。 
但是，减完以后我们会发现蓝色阴影部分的矩阵被减了两次，很明显减多了，所以我们还需要加上sum(x1-1,y1-1) 
这样就成了我给的公式。