论文笔记:Learning Denoising from Single Noisy Images
Introduction
上次看过文章Noise2Noise(简称为N2N吧),其使用noisy-noisy image pairs对网络进行训练,可以达到使用noisy-clean image pairs的效果。但在N2N中,使用的noisy-noisy image pairs要求有相同的图像内容带有不同的噪声,即 ( s + n , s + n ′ ) (s+n, s+n') (s+n,s+n′),其中 s s s是图像信号, n n n和 n ′ n' n′是相互独立的噪声。也就是说我们对同一场景要获得两张以上的噪声图像才能进行训练。那能不能只有一张噪声图像就可以训练网络进行去噪呐?最近看到网上出了好几篇文章都是对这个问题进行讨论的。我看到了三篇分别是《Noise2Void - Learning Denoising from Single Noisy Images》、《SELF-SUPERVISED DEEP IMAGE DENOISING》、《Noise2Self: Blind Denoising by Self-Supervision》,文章链接放在最后了。我只通读了第一篇,后两篇只大体浏览了一下,虽然方法不同,但内容和效果也有相似之处。下面重点介绍一下第一篇Noise2Void(简称N2V)。
Method
对于一张带噪声的图像 x = s + n x=s+n x=s+n,作者做了两个假设:
(1) 信号 s s s是像素相关的。
p ( s i ∣ s j ) ≠ p ( s i ) p(s_i|s_j) \neq p(s_i) p(si∣sj)̸=p(si)
这个不难理解,图像信号的像素不是相互独立的,这也是为什么我们能用各种滤波器对图像进行平滑滤波去噪的原因。
(2) 噪声 n n n在给定信号 s s s的条件下是像素无关的。
p ( n ∣ s ) = ∏ i p ( n i ∣ s i ) p(n|s)=\prod_i p(n_i|s_i) p(n∣s)=i∏p(ni∣si)
也就是说各个像素之间的噪声是独立同分布的。
除此之外,作者还做了和N2N相同的一个假设,即噪声的均值为0,
E [ n i ] = 0 , E [ x i ] = s i E[n_i]=0, E[x_i]=s_i E[ni]=0,E[xi]=si
也就是说如果能对同一个信号获取多张有不同噪声的图像,对它们取平均可以接近真实的信号值。
Supervised Training
一般我们用来做去噪的网络都是CNN,进一步说是全卷积网络(FCN)。对于一个FCN来说,网络输出的每一个像素的预测值 s ^ i \hat{s}_i s^i都有一个确定的感受野 x R F ( i ) x_{RF(i)} xRF(i)。也就是说输入图像的一个范围内的像素都会对输出预测值有形象。
![]()
基于这个想法,可以把去噪网络看做一个函数 f f f,其输入是一个patch x R F ( i ) x_{RF(i)} xRF(i),输出是一个位于位置 i i i的像素 s ^ i \hat{s}_i s^i,
f ( x R F ( i ) ; θ ) = s ^ i f(x_{RF(i)};\theta)=\hat{s}_i f(xRF(i);θ)=s^i
其中, θ \theta θ表示网络参数。
在传统监督学习中,使用noisy-clean image pairs ( x j , s j ) (x^j, s^j) (xj,sj)对网络进行训练,就可以表示为
arg min θ ∑ j ∑ i L ( f ( x R F ( i ) j ; θ ) = s ^ i j , s i j ) \arg\min_{\theta} \sum_j\sum_i L(f(x^j_{RF(i)};\theta)=\hat{s}^j_i,s^j_i) argθminj∑i∑L(f(xRF(i)j;θ)=s^ij,sij)
在N2N中,使用noisy-noisy image pairs ( x j , x ′ j ) (x^j, x'^j) (xj,x′j)对网络进行训练,其中
x j = s j + n j , x ′ j = s j + n ′ j x^j=s^j+n^j, x'^j=s^j+n'^j xj=sj+nj,x′j=sj+n′j
噪声部分都来自于同一个噪声分布的独立采样。虽然网络学习得是从一张噪声图像到另一张噪声图像的映射,但训练仍然能够收敛到正确的解。这个现象的关键在于噪声图像的期望值等于干净的图像。
在N2V训练中,只有单张噪声图像 x j x^j xj,如果只是简单得提取一个patch作为输入,而用其中心像素作为目标进行训练,网络将只会学到恒等映射,即直接把输入patch的中心值映射到输出。为此,文章设计了一种有着特殊感受野的网络结构——盲点网络(blind-spot network)。如下图所示,该网络的感受野中心是一个盲点。网络的预测值 s ^ i \hat{s}_i s^i受其邻域所有输入像素的影响,除了其自身位置的输入像素 x i x_i xi。

该网络的优点在于其不会学到恒等映射。因为我们假设了噪声在像素间是不相关的,所以只利用邻域信息是不能恢复噪声的,而只能恢复图像信息。也因此网络不能产生比期望值更好的估计结果。
当然,文章也提到了,由于该网络在预测时并没有使用所有可用信息,所以其结果精确度可能比起正常网络会有略微的下降。
文章也提出在实际使用中,为了网络的有效性,并不直接使用该网络,而是使用一种等价策略:在每个输入patch中,随机选择一个邻域值替代中心像素。如下图所示。

在具体应用中,文章仿照CARE的设置,使用U-net结构,并在每个激活层之前加入batch normlization。
Experiment Results
文章与现有的方法做了对比,结果如下图。可以看出,虽然结果略逊于传统N2C(Noise2Clean),N2N方法,但比起BM3D还有有一定优势。
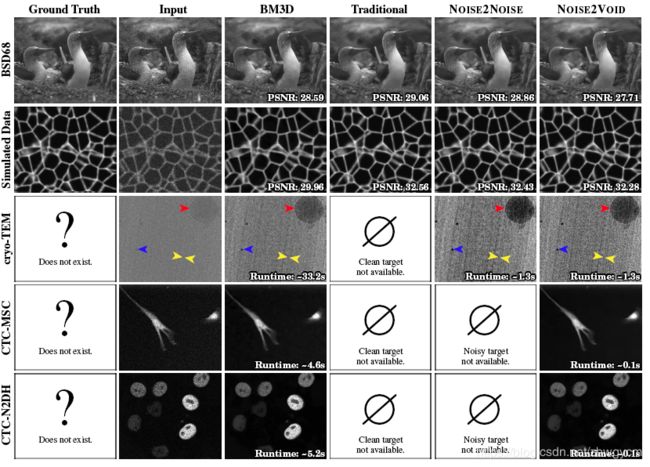
Errors and Limitations
文章在一开始便做出了一些先验假设,不满足这些假设的情况当然会出现错误。
如下图所示,在第一行中,孤立的白点与其邻域像素相比是独立的,所以不能用其邻域像素正确地预测。也就是说信号要有可预测性。同样,在第二行中,许多纹理细节也因不能正确地预测而丢失了。

除此之外,如下图所示,N2V不能区分信号和结构性噪声,这违反了噪声是像素独立的假设。

Something More
整体来说,N2V提出了一种新的思路,使用单张噪声图像来训练去噪网络。其关键在于建立盲点网络,避免网络变成恒等映射。同样地思路也出现在《SELF-SUPERVISED DEEP IMAGE DENOISING》文章中,只不过其用了另一种方式来实现盲点网络。除此之外,《SELF-SUPERVISED DEEP IMAGE DENOISING》还利用最大后验概率的方法将被去掉的像素给利用起来,增加输入信息,从而提高结果质量。
在《Noise2Self: Blind Denoising by Self-Supervision》中,文章主要证明了在一定条件下( g θ ( x ) g_{\theta}(x) gθ(x)的值不依赖于 x x x),损失函数
L ( g θ ) = E ∥ g θ ( x ) − x ∥ 2 L(g_{\theta})=E\| g_{\theta}(x)-x \|^2 L(gθ)=E∥gθ(x)−x∥2
是可以取得除恒等映射外的最优解的。且对于传统的去噪函数 f θ f_{\theta} fθ可以变为 g θ g_{\theta} gθ,使得损失函数
L ( f θ ) = E ∥ f θ ( x ) − y ∥ 2 L(f_{\theta})=E\| f_{\theta}(x)-y \|^2 L(fθ)=E∥fθ(x)−y∥2
与
L ( g θ ) = E ∥ g θ ( x ) − x ∥ 2 L(g_{\theta})=E\| g_{\theta}(x)-x \|^2 L(gθ)=E∥gθ(x)−x∥2
在相同参数 θ \theta θ下取得最优解。
这三篇论文基于相同的假设,即噪声在像素间是独立同分布的,且主要都是基于邻域像素去预测当前像素值。我没有仔细地阅读文章(主要是很多地方还看不懂……),理解地可能有偏差,具体内容请参考原文。
参考文献:
- Noise2Void - Learning Denoising from Single Noisy Images [arxiv]
- SELF-SUPERVISED DEEP IMAGE DENOISING [arxiv]
- Noise2Self: Blind Denoising by Self-Supervision [arxiv] [github]