机器学习 局部加权回归及Python简单实现

一、欠拟合与过拟合

加入对给定的一组样本x_i和真实值y_i，假如合适的特征应选为x1=x_i，x2=x_i²，预测值$h\theta (x_i)$=${\sum }_{i=0}^{i=2}{\theta }_i{x}_i$=${\theta }_0+{\theta }_1{x}_i+{\theta }_2{x}_i^2$，这样拟合出的曲线较为合适。则若把特征选为x1=x_i，预测值$h\theta (x_i)$=${\sum }_{i=0}^{i=1}{\theta }_i{x}_i$=${\theta }_0+{\theta }_1{x}_i$，就会丢失二次项，预测曲线与输入值的真实值可能会有较大的误差。此类拟合方式称为欠拟合。
而若把特征选为x1=x_i，x2=x_i²…x6=x_i⁶，预测值$h\theta (x_i)$=${\sum }_{i=0}^{i=6}{\theta }_i{x}_i$=${\theta }_0+{\theta }_1{x}_i+{\theta }_2{x}_i^2...+{\theta }_6{x}_i^6$，则对于给定的样本，预测曲线几乎完美符合。这是因为当特征数量较大，甚至大到与样本数量较接近时，接近直接解出多元高次方程，损失函数几乎失去意义。这会导致虽然预测曲线完美符合训练样本，但样本外的一般性输入，预测值会与真实值偏差值极大。此类拟合称为过拟合。
因此梯度下降等参数学习需要合适选取特征集，避免欠拟合和过拟合。

二、局部加权的原因

梯度下降回归多元线性回归的预测值$h_{\theta }(x)$为${\sum }_{i=0}^{i=n}{\theta }_i{x}_i$（定义$x_0$=1，有x1~xn共n个特征)。
当要计算一个给定的检测点$\widehat{x_k}$的预测值时，多元线性回归会先求出使$\frac{1}{2}{\sum }_{i=1}^{i=m}(h_{\theta }(x_i)-y_i{)}^2$即m个样本的损失函数最小的$\hat{\theta }$=$[{\theta }_0,{\theta }_1...{\theta }_n{]}^T$，再计算$h_{\theta }(x_k)$=${\hat{\theta }}^T{\hat{X}}_k$=${\sum }_{i=0}^{i=n}{\theta }_i{x}_{ki}$。
此类学习被称为参数学习，即先求出样本整体满足预设条件参数向量再给出检测点的判断值。这会导致参数向量可能在整体上的符合度较好，但在某些局部检测点符合度很差。
有另一类学习称为非参数学习，即不求样本整体满足预设条件的参数向量，而是针对某个特定的局部检测点求参数向量，并用求得的参数向量计算在该特定局部检测点的预测值。局部加权回归就是一种非参数学习。
局部加权回归在计算给定的检测点$\widehat{x_k}$的预测值时，会计算使损失函数J($\theta$)=$\frac{1}{2}{\sum }_{i=0}^{i=m}{w}_i(h_{\theta }(x_i)-y_i{)}^2$最小的$\hat{\theta }$。w_i即为权重，常用的为w_i=exp{$\frac{-(x_i-x_k{)}^2}{2}$}。此权重的特点是当|x_i-x_k|较小的时候，即在检测点$\widehat{x_k}$附近，w_i ->1 ，权重较大，当|x_i-x_k|较大的时候，即在检测点$\widehat{x_k}$较远处，w_i ->0，权重较小。当然，权值函数不一定为指数衰减函数，也可以为其他的函数，如w_i=exp{$\frac{-(x_i-x_k{)}^2}{2\tau }$}，通过控制$\tau$的值控制指数衰减的速度，当$\tau$较小时衰减快，较大衰减快。权值函数可以任选，但一定是检测点附近权值大，较远处权值小。
非参数学习可以削弱选取特征集带来的影响，减少欠拟合与过拟合，让我们相对更少地花费时间精力在选取合适特征集上。
局部加权回归使得检测点主要依赖于它附近（旁边）的样本，假如一个总体分布曲线呈钟形，用直线，二次项，三次项等拟合时可能会导致检测点预测值与真实值差距极大。这是因为拟合值更倾向适应整体。而若仅仅选取检测点局部进行拟合，拟合曲线倾向于适应该检测点的局部，预测值与真实值偏差会较小。
由于局部加权回归对任何检测点都需要把训练集整体加权拟合一遍，即每次做出预测都要根据整个训练集在检测点附近加权拟合一遍（这是因为非参数学习未使用某组固定的参数）因此训练集需保留，且当训练集较大时，用局部加权回归做出预测虽然更精确但时间花费较多。
局部加权并没有完全避免过拟合和欠拟合的问题。若权值函数选取不当，依然会有过拟合和欠拟合的问题。但相对于参数学习，过拟合和欠拟合问题已经减轻，在特定局部检测点的预测精度较好。

三、局部加权回归

预测函数$h_{\theta }(x_i)$=${\sum }_{i=0}^{i=n}{\theta }_i{x}_i$，权重函数w_i=exp{$\frac{-(x_i-x_k{)}^2}{2{\tau }^2}$}，损失函数J($\theta$) = $\frac{1}{2}{\sum }_{i=0}^{i=m}{w}_i(h_{\theta }(x_i)-y_i{)}^2$，每次用梯度下降进行迭代时，${\theta }_{k+1}={\theta }_k+\alpha ▽J(\theta )$，$▽J(\theta )$ =${\sum }_{i=1}^{m}wi\ast$($h_{\theta }$(x_i) - y_i) [x₀$\frac{\widehat{{\theta }_0}}{|{\hat{\theta }}_0|}$, x_i1$\frac{\widehat{{\theta }_1}}{|{\hat{\theta }}_1|}$,x_i2$\frac{\widehat{{\theta }_2}}{|{\hat{\theta }}_2|}$,…x_in$\frac{\widehat{{\theta }_n}}{|{\hat{\theta }}_n|}$]^T ，因此每次迭代时${\theta }_{k+1}={\theta }_k+\alpha ▽J(\theta )$=${\theta }_k$+$\alpha {\sum }_{i=1}^{m}wi\ast$($h_{\theta }$(x_i) - y_i) [x₀$\frac{\widehat{{\theta }_0}}{|{\hat{\theta }}_0|}$, x_i1$\frac{\widehat{{\theta }_1}}{|{\hat{\theta }}_1|}$,x_i2$\frac{\widehat{{\theta }_2}}{|{\hat{\theta }}_2|}$,…x_in$\frac{\widehat{{\theta }_n}}{|{\hat{\theta }}_n|}$]^T
（更详细的步骤在梯度学习数学原理中已提到，原文链接https://blog.csdn.net/ShiZhanfei/article/details/84345278）
至此，局部加权回归的预测函数，损失函数，权重函数，梯度函数均已得到。

四、一个简单的局部加权回归预测

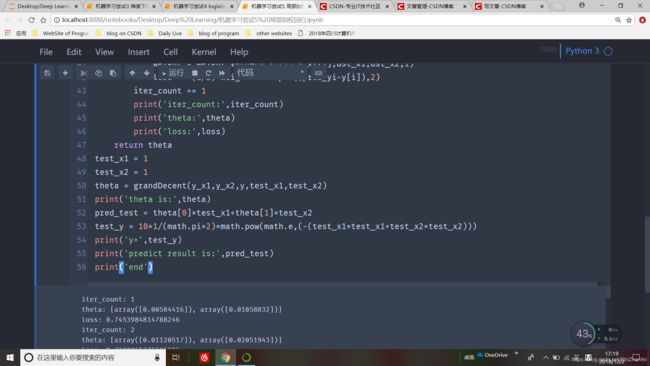
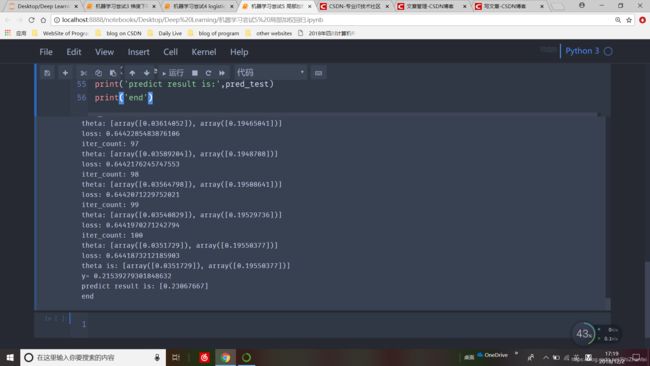
import numpy as np
import math
#把特征选取为两个标准正态分布
y_x1_mu,y_x1_sigma = 0,2#分类结果为1的y的x1的均值和方差
y_x1 = list(np.random.normal(y_x1_mu,y_x1_sigma,20))#正态分布中取20个随机数
y_x2_mu,y_x2_sigma = 0,3#分类结果为1的y的x2的均值和方差
y_x2 = list(np.random.normal(y_x2_mu,y_x2_sigma,20))
y = np.zeros((20,1))
# 把输出选定为相互独立的二维正态分布加上一个微小标准正态的扰动
for i in range(0,20):
    y[i] = 10*1/(math.pi*2)*math.pow(math.e,(-(y_x1[i]*y_x1[i]+y_x2[i]*y_x2[i])))+np.random.normal(0,1)/10
#权值函数，输入x在检测值dst_x处的权重，权重参数为t，下面计算权重时都把t取为1
def weight_value(xi_1,xi_2,dst_xi_1,dst_xi_2,t):
    return math.pow(math.e,((-(xi_1-dst_xi_1)*(xi_1-dst_xi_1)-(xi_2-dst_xi_2)*(xi_2-dst_xi_2))/(2*t*t)))
#梯度下降函数计算在检测点处的参数
def grandDecent(x1,x2,y,dst_x1,dst_x2):
    loss = 1
    theta = [0,0]
    step_size = 0.01
    finish_loss = 0.001
    iter_count = 0
    max_iters = 100
    while loss>finish_loss and iter_count

运行结果如下


实际应用中，应选取更恰当的参数。

五、概率论解释损失函数每项差值要取平方的原因

现在，把检测点x_i的真实值定为y_i=$({\hat{\theta }}_i{)}^T{x}_i$+${ϵ}_i$，${ϵ}_i$表示原拟合$({\hat{\theta }}_i{)}^T{x}_i$未捕获某些东西导致的误差，可能为未捕获的高次项特征，也可能为未捕获的其他特征，或是随机噪声等。${ϵ}_i\sim N(0,{\sigma }^2)$
中心极限定理告诉我们生活中大量存在正态分布，若把真实值y_i视为多个随机变量的叠加，则当随机变量数量较多时（事实上生活中充满随机变量）y_i依分布收敛于正态分布，对y_i进行标准化后分布即为标准正态(即$\frac{y_i-E(y_i)}{\sqrt{D(y_i)}}\sim N(0,1)$ ).。因此，当$({\hat{\theta }}_i{)}^T$确定，x_i确定后，P{y_i=k}=$\frac{1}{\sqrt{2\pi }\sigma }$exp{ $-\frac{(k-\hat{\theta }{x}_i{)}^2}{2{\sigma }^2}$} 即y_i $\sim N(\hat{\theta }{x}_i,{\sigma }^2)$
由于样本之间相互独立，因此误差项${ϵ}_i$相互独立且同分布。定义似然性函数L($\theta$)=${\prod }_{i=1}^{i=m}P${Y=yi}=${\prod }_{i=1}^{i=m}\frac{1}{\sqrt{2\pi }\sigma }exp${-$\frac{(yi-(\hat{\theta }{)}^T{\hat{x}}_i{)}^2}{2{\sigma }^2}$}，该函数描述了给定$\hat{\theta }$后，对整体样本值而言真实值yi的整体概率。该函数值越大，则选定的$\hat{\theta }$使得样本值接近真实值的概率越大。则由概率论与数理统计中参数选取的似然性最大原则，即选择使结果可能性最高的参数，应选取使L($\theta$)最大的$\hat{\theta }$
为数学方便，选取l($\theta$)=ln [L($\theta$)] = ln [ ${\prod }_{i=1}^{i=m}P${Y=yi}=${\prod }_{i=1}^{i=m}\frac{1}{\sqrt{2\pi }\sigma }exp${-$\frac{(yi-(\hat{\theta }{)}^T{\hat{x}}_i{)}^2}{2{\sigma }^2}$}] = m*ln($\frac{1}{\sqrt{2\pi }\sigma }$) + ${\sum }_{i=1}^{i=m}-\frac{(y_i-(\hat{\theta }{)}^T{\hat{x}}_i{)}^2}{2{\sigma }^2}$
因此等效于使${\sum }_{i=1}^{i=m}\frac{(y_i-(\hat{\theta }{)}^T{\hat{x}}_i{)}^2}{2}$最小。注意到这个表达式事实上就是损失函数J($\theta$)。到此，给出了概率角度对线性回归的表述。通过假设误差服从正态分布（由中心极限定理可知该假设有概率论的数学支持），可以得到$\hat{\theta }$的选择标准应该是使得函数J($\theta$)=${\sum }_{i=1}^{i=m}\frac{(y_i-(\hat{\theta }{)}^T{\hat{x}}_i{)}^2}{2}$最小。

2018/12/2