
凌云时刻 · 技术


导读:这篇笔记主要介绍梯度下降法,梯度下降不是机器学习专属的算法,它是一种基于搜索的最优化方法,也就是通过不断的搜索然后找到损失函数的最小值。像上篇笔记中使用正规方程解实现多元线性回归,基于这个模型我们可以推导出 的数学解,但是很多模型是推导不出数学解的,所以就需要梯度下降法来搜索出最优解。
作者 | 计缘
来源 | 凌云时刻(微信号:linuxpk)
梯度下降法概念

我们来看看在二维坐标里的一个曲线方程:
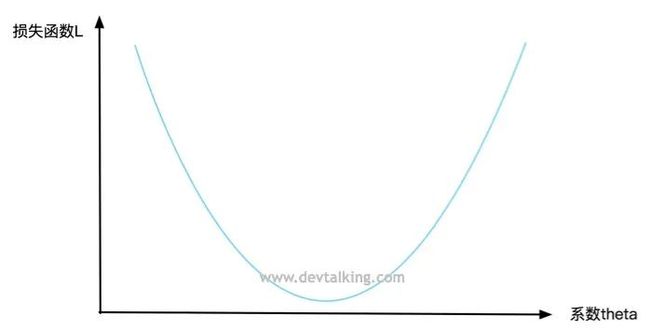
纵坐标表示损失函数L的值,横坐标表示系数 。每一个
的值都会对应一个损失函数L的值,我们希望损失函数收敛,既找到一个 的值,使损失函数L的值最小。
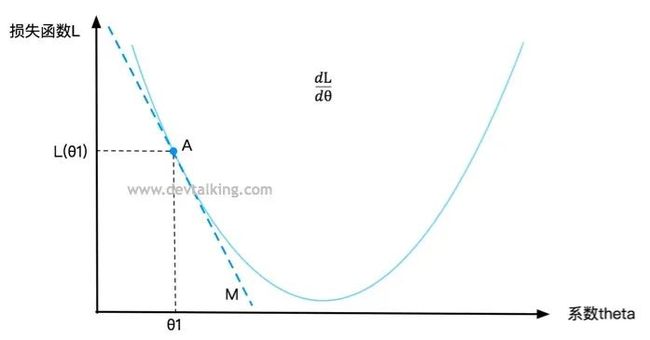
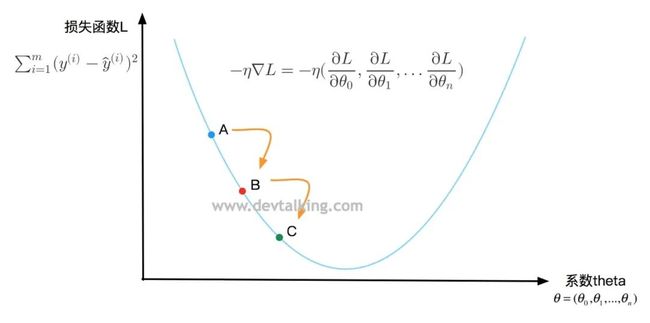
在曲线上定义一点A,对应一个 值,一个损失函数L的值,要判断点A是否是损失函数L的最小值,既求该点的导数,在第一篇笔记中我解释过,点A的导数就是直线M的斜率,直线M是点A的切线,所以导数描述了一个函数在某一点附近的变化率,并且导数大于零时,函数在区间内单调递增,导数小于零时函数在区间内单调递减。所以 表示损失函数L增大的变化率, 表示损失函数L减小的变化率。
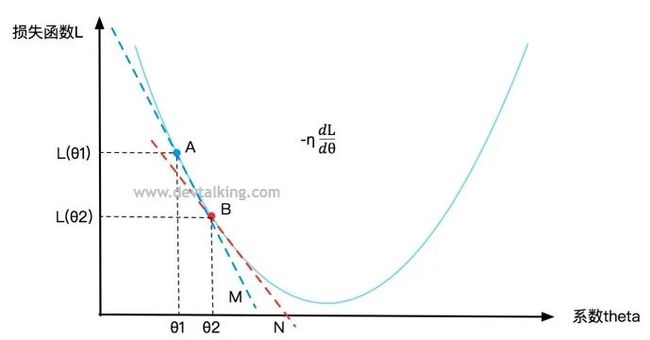
再在曲线上定义一点B,在点A的下方,B点的 值就是A点的 值加上让损失函数L递减的变化率 , 称为步长,既B点在 变化率的基础下移动了多少距离,在机器学习中 这个值也称为学习率。
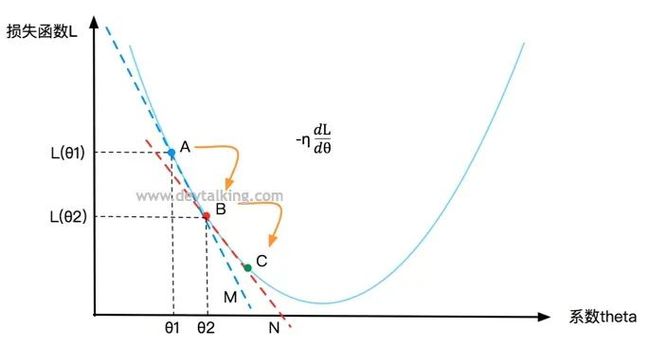
同理还可以再求得点C,然后看是否是损失函数的L的最小值。所以梯度下降法就是基于损失函数在某一点的变化率 ,以及寻找下一个点的步长 ,不停的找到下一个点,然后判断该点处的损失函数值是否为最小值的过程。 就称为梯度。
在第一篇笔记中将极值的时候提到过,当曲线或者曲面很复杂时,会有多个驻点,既局部极值,所以如果运行一次梯度下降法寻找损失函数极值的话很有可能找到的只是局部极小值点。所以在实际运用中我们需要多次运行算法,随机化初始点,然后进行比较找到真正的全局极小值点,所以初始点的位置是梯度下降法的一个超参数。
不过在线性回归的场景中,我们的损失函数 是有唯一极小值的,所以暂时不需要多次执行算法搜寻全局极值。
 梯度下降的步长
梯度下降的步长
步长在梯度下降法中非常重要,这里着重说一下。
在机器学习中称为学习率(Learning rate)。
的取值影响获得最优解的速度。想象一下如果 过小,那么寻找的点就会变得很多,收敛速度下降。如果 过大可能会不断错过最优解,同样影响收敛速度。
取值不合适时甚至得不到最优解。比如 值过大会造成损失函数值越来越大。
也是梯度下降法的一个超参数。可能会有搜索最佳 的过程。
实现梯度下降法

我们在Jupyter Notebook中来看看如何实现梯度下降法:
import numpy as np
import matplotlib.pyplot as plt
# 模拟theta值,及确定一个损失函数
plot_x = np.linspace(-1, 6, 100)
plot_y = (plot_x-2.5)**2-1
# 将该曲线绘制出来
plt.plot(plot_x, plot_y)
plt.show()
|

下面我们来定义变化率 和损失函数:
# 变化率
def dL(theta):
# 对(theta-2.5)**2-1 求导,然后返回
return 2*(theta-2.5)
# 损失函数
def L(theta):
return (theta-2.5)**2-1
|
然后来看看实现梯度下降的过程:
# 步长默认设为0.1
eta = 0.1
# 初始点默认设为0.0
theta = 0.0
# 找到的新的theta值与上一个theta值的差值最小边界
difference = 1e-8
while True:
# 求出梯度,既变化率
gradient = dL(theta)
# 记录上一个theta值
last_theta = theta
# 寻找下一个theta值,既当前的theta值加上乘以步长的使损失函数递减的变化率
theta = theta - eta*gradient
# 当新找到的theta值与上一个theta值之差小于1e-8时,表明此时变化率已经趋于0了,新的theta值可以使损失函数达到极小值
if(abs(L(theta) - L(last_theta)) < difference):
break
print(theta)
print(L(theta))
# 结果
2.499891109642585
-0.99999998814289
|
得到的 值为2.5,损失函数的极小值为-1,代入方程 可验证我们的求解是正确的。
 Theta的变化
Theta的变化
我们将每次 的值记下来,然后描绘出来,看看是如何变化的:
eta = 0.1
difference = 1e-8
theta = 0.0
theta_history = [theta]
while True:
gradient = dL(theta)
last_theta = theta
theta = theta - eta * gradient
theta_history.append(theta)
if(abs(L(theta) - L(last_theta)) < different):
break
len(theta_history)
# 结果
46
plt.plot(plot_x, L(plot_x))
plt.plot(np.array(theta_history), L(np.array(theta_history)), color='r', marker='+')
plt.show()
|
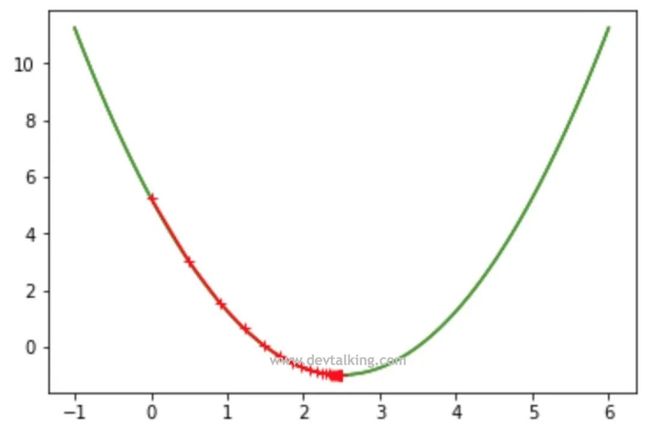
从上面的示例代码中看到,一共经历了45次的查找得到了让函数达到最小值的 。并且看到一开始因为曲线比较陡,所以梯度比较大,两个点之间的间隔比较大,到曲线底部的时候因为曲线开始平缓,梯度逐渐变小,每个点之间的间隔就越来越小。
我们将步长调大一些,看看 的查找轨迹是怎样的:
eta = 0.8
difference = 1e-8
theta = 0.0
theta_history = [theta]
while True:
gradient = dL(theta)
last_theta = theta
theta = theta - eta * gradient
theta_history.append(theta)
if(abs(L(theta) - L(last_theta)) < difference):
break
plt.plot(plot_x, L(plot_x))
plt.plot(np.array(theta_history), L(np.array(theta_history)), color="r", marker="+")
plt.show()
|
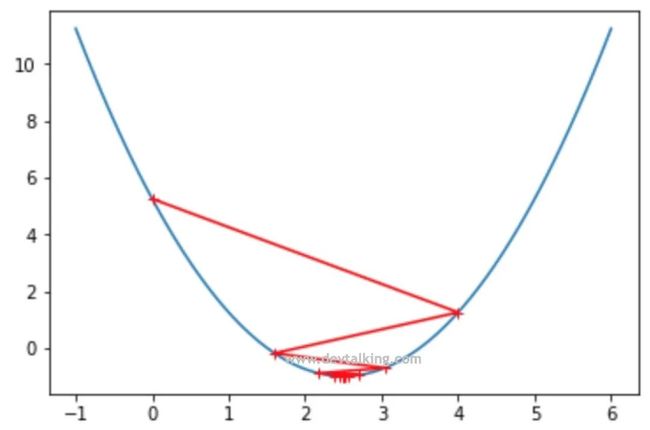
从图中可以看到,第一次查找的时候就越过了极值点,找到了曲线另一侧的点,不过好在损失函数的值还是递减的状态所以最终还是找到了极值点。
我们将步长再调大点,看会发生什么情况:
def L(theta):
try:
return (theta-2.5)**2-1
except:
return float('inf')
eta = 1.1
difference = 1e-8
theta = 0.0
theta_history = [theta]
n_iters = 100
i_iter = 0
while i_iter < n_iters:
gradient = dL(theta)
last_theta = theta
theta = theta - eta * gradient
theta_history.append(theta)
if(abs(L(theta) - L(last_theta)) < difference):
break
i_iter += 1
plt.plot(plot_x, L(plot_x))
plt.plot(np.array(theta_history), L(np.array(theta_history)), color="r", marker="+")
plt.show()
|
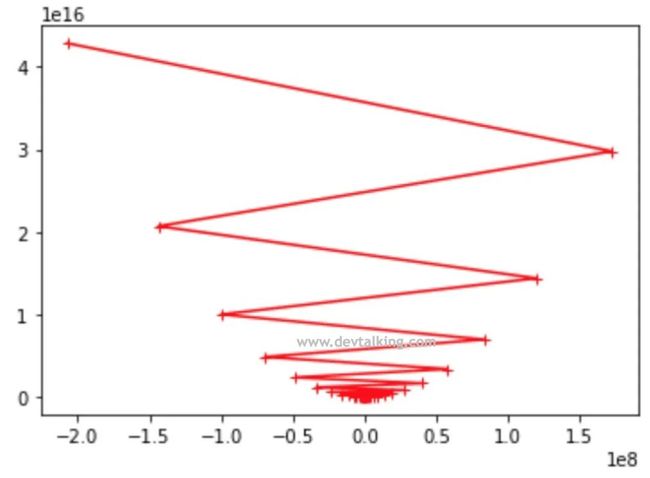
从图中看到每次找到的 会使损失函数越来越大,根本无法找到极小值。所以步长的确定非常重要,不过一般情况下,我们将步长设为0.01是比较保险的做法,但是如果想使算法在各方面达到最优,那么还是需要先对步长这个超参数进行严谨的确定。
 求导概念复习
求导概念复习
在看如何使用梯度下降解决线性回归问题前,我们先来复习一下求导的知识。
 代数函数的求导
代数函数的求导
 一般求导定则
一般求导定则
线性定则
乘法定则
除法定则
( )
倒数定则
( )
复合函数求导法则
线性回归中使用梯度下降法

上一节通过一维场景解释了梯度下降法,这一节在高维的场景中看看如何使用梯度下降法解决线性回归的问题。
在线性回归的问题中注意一下三个方面:
首先损失函数 是明确的,前面用正规方程解实现的时候已经推导过。
其次系数 不是一维的了,而是多维的,即 是一个向量。
最后损失函数不是对一维系数 求全导,而是对 求导数,记为 ,即梯度。
在上一篇笔记中我们推导过 的函数:
所以代入损失函数后就得:
在讲正规方程解时我们推导过,上面的函数可以转换为:
我们的目标就是让上面的函数尽可能的小,根据之前讲过的概念,我们知道损失函数的梯度就是对 向量中的每个 求导,并且在上篇笔记中我们知道 向量是一个列向量,根据复合函数求导定则,所以损失函数L的梯度为:
将2提到外面,然后将后面的负号移进前面的括号里得:
可以发现上面公式中每个元素都经过了m求和,这样带来的问题就是梯度受样本数据数量的影响极大,不过在线性回归的评测标准一节中讲到的均方误差MSE就是为了解决这个问题的,所以我们将损失函数直接转变为MSE:
那么对MSE求梯度的结果自然也是损失函数求梯度后乘以1/m:
实现线性回归中的梯度下降法

我们先在Jupyter Notebook中来实现,然后再在PyCharm中进行封装:
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子
np.random.seed(666)
# 随机构建100个数
x = 2 * np.random.random(size=100)
# 拟定一个线性方程,x乘3乘4后再加上随机生成的正态分布数
y = x * 3. + 4. + np.random.normal(size=100)
# 先从100行1列的矩阵开始,既样本数据只有一个特征
X = x.reshape(-1, 1)
plt.scatter(x, y)
plt.show()
|
# 定义损失函数
def L(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta))**2) / len(X_b)
except:
return float('inf')
# 定义梯度
def dL(theta, X_b, y):
# 开辟空间,大小为theta向量的大小
gradient = np.empty(len(theta))
# 第0元素个特殊处理
gradient[0] = np.sum(X_b.dot(theta) - y)
for i in range(1, len(theta)):
# 矩阵求和可以转换为点乘
gradient[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
return gradient * 2 / len(X_b)
# 梯度下降法
def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, difference = 1e-8):
theta = initial_theta
i_iter = 0
while i_iter < n_iters:
gradient = dL(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if(abs(L(theta, X_b, y) - L(last_theta, X_b, y)) < difference):
break
i_iter += 1
return theta
# 构建X_b
X_b = np.hstack([np.ones((X.shape[0], 1)), X])
# 初始化theta向量为元素全为0的向量
initial_theta = np.zeros(X_b.shape[1])
# 设置步长为0.01
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)
theta
# 结果
array([ 4.02145786, 3.00706277])
|
可以看到我们得到的结果,解决为4,斜率为3,和我们拟定的线性方程是一致的。
下面我们在PyCharm中封装梯度下降法。在LinearRegression类中再增加一个fit_gd方法,和fit_normal方法区分开,表明是用梯度下降法进行训练:
# 使用梯度下降法,根据训练数据集X_train,y_train训练LinearRegression模型
def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
assert X_train.shape[0] == y_train.shape[0], \
"特征数据矩阵的行数要等于样本结果数据的行数"
# 定义损失函数
def L(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / len(X_b)
except:
return float('inf')
# 定义梯度
def dL(theta, X_b, y):
# 开辟空间,大小为theta向量的大小
gradient = np.empty(len(theta))
# 第0元素个特殊处理
gradient[0] = np.sum(X_b.dot(theta) - y)
for i in range(1, len(theta)):
# 矩阵求和可以转换为点乘
gradient[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
return gradient * 2 / len(X_b)
# 梯度下降法
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, difference=1e-8):
theta = initial_theta
i_iter = 0
while i_iter < n_iters:
gradient = dL(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(L(theta, X_b, y) - L(last_theta, X_b, y)) < difference):
break
i_iter += 1
return theta
# 构建X_b
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
# 初始化theta向量为元素全为0的向量
initial_theta = np.zeros(X_b.shape[1])
self._theta = gradient_descent(X_b, y_train, initial_theta, eta)
self.intercept_ = self._theta[0]
self.coef_ = self._theta[1:]
return self
|
END

往期精彩文章回顾

机器学习笔记(九):多元线性回归
机器学习笔记(八):线性回归算法的评测标准
机器学习笔记(七):线性回归
机器学习笔记(六):数据归一化
机器学习笔记(五):超参数
机器学习笔记(四):kNN算法
机器学习笔记(三):NumPy、Matplotlib、kNN算法
机器学习笔记(二):矩阵、环境搭建、NumPy
机器学习笔记(一):机器的学习定义、导数和最小二乘
Kafka从上手到实践 - 实践真知:搭建Kafka相关的UI工具

长按扫描二维码关注凌云时刻
每日收获前沿技术与科技洞见
![]()
![]()
![]()
![]()
 梯度下降的步长
梯度下降的步长![]()
 Theta的变化
Theta的变化 求导概念复习
求导概念复习![]() 代数函数的求导
代数函数的求导![]() 一般求导定则
一般求导定则![]()
![]()
![]()
![]()
![]()









