你真的明白神经网络是什么?
前两天有网友找我,让我解释下神经网络到底是什么东东。这位朋友他学习了吴恩达大神的深度学习课程,对神经网络、神经元、激活函数、损失函数等都有所了解,他以为自己已经搞懂了什么是AI,但细想之下发现自己竟然连神经网络的概念都讲不清楚。
对于这个问题,一开始我也是有些蒙圈的,我知道它是什么但却无法给出清晰准确的定义,这篇博文就是我对神经网络再学习的知识总结,希望能对同样困惑的朋友有所帮助。
神经网络是函数
在Michael Nielsen大神的著作 Neural Networks and Deep Learning的chapter 4: A visual proof that neural nets can compute any function
,他论证了在通用逼近理论(universal approximation theorem)的作用下,只要神经网络足够大(隐层神经元足够多),它可以逼近任意函数(can compute any function)。
机器学习,实际上是寻找一种数学模型,让这个模型符合它所要描述的对象。比如说我们要寻找一个能区分出Figure 1中蓝色和橙色点的模型,用它可以区分现有的以及未来可能新增的点,这个数学模型就是图中的白线,即ax + b = y,只要计算出a和b,就可以用函数ax + b来解决Figure 1的分类问题。
理论上说,神经网络可以逼近任意函数,即找到解决任何难题对应的数学模型,而且隐层的神经元数越多就越逼近目标函数。例如,对于同一个神经网络,用猫狗图片的数据集训练它,它就是可以判断你给它看的是猫的还是狗的图片,如果你用它来训练英文文本,它就可以根据你提供的一段英文句子来预测下一个最有可能出现的英文单词。所以说,神经网络是函数,一种无限灵活的数学模型生成函数。
神经网络是Linearity + Non-Linearity
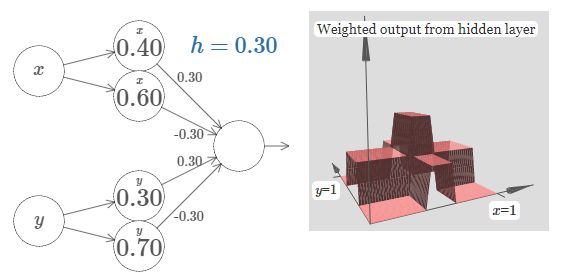
从网络架构来看,神经网络中的隐层是由线性层+非线性层构成,线性层是权值矩阵,非线性层则是激活函数。在linearity + non-linearity的结构下,逼近理论(universal approximation theorem)就会起作用,非线性层将线性层中矩阵计算的结果转化为step function,一个个神经元的step function构成了一个个小箱子(bumps),通过调节Figure 2中神经元权值的大小来调节箱子的长宽高,进而改变整个图形的形状,以逼近任意的曲面(或函数)。
损失函数是衡量逼近效果的量化工具
以Figure 1的数学模型ax + b为例,假设在初始化时给a和b赋随意值,神经网络的训练就是要调整a和b以改变白线的位置和方向,至于如何调整a、b,是增加还是减少,增减的量是多少,这些信息是通过函数对a、b求导得到的。
损失函数是用于计算神经网络生成的函数和真实函数(ground true)的差异值。假设在Figure 2的3D图形中叠加一个相似的图形,两个图形之差的体积就是损失函数的计算结果,也称为损失值–loss,loss值越小表示模型逼近效果越好。通过loss对神经元权值求导,可以知道按照对应导数来调整权值大小的同时会对图形产生什么样的改变。
当然,损失函数并不是唯一的,常用的有MSE(mean square error)、MAE(L1 loss, mean absolute error)、NLLoss(Negative log likelihood function)等,不同的损失函数计算的loss值也会不同,也就是说,神经元权值发生调整后,新图形的形状也会各不相同。现实情况是,根据不同的任务以及神经网络训练的不同阶段,可以采用不同的损失函数。例如MSE是神经网络默认的loss function,而线性回归问题用NLLoss比MSE更好,SSD中预测bounding box的模型则采用的是MAE。
总的来说,损失函数决定了函数形状以及每次调整形状的方向,在神经网络训练过程中可以采用不同损失函数。它就好比是我们平时生活中制定的各种目标,不管我们是采用目标拆解还是目标迂回的方法,最重要的是我们制定的这些目标要准确。损失函数也一样,如果没有选对损失函数,最终生成的函数和解决问题需要的数学模型就会有偏差,loss值越大偏差越大。
手写体数字识别 / Notebook
接下来我希望通过一个实例来帮助加深对上述知识的理解。手写体数字识别算是神经网络的“Hello World”程序,我会用Pytorch来实践这个实例,大部分源码来自Pytorch的官方sample,我简化它的神经网络模型,并剔除了与主体无关的代码片段,同样的,我不会详述Pytorch的具体使用,如果你不是很了解Pytorch,请结合Pytorch的tutorials学习,请放心,Pytorch很好上手。
Dataset
train_loader = torch.utils.data.DataLoader(
datasets.MNIST(PATH, train=True, download=True, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])), batch_size=bs, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST(PATH, train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])), batch_size=bs, shuffle=True, **kwargs)
Pytorch已经提供了MNIST数据集,只要调用datasets.MNIST()下载即可,这里要注意的是标准化(Normalization):
transforms.Normalize((0.1307,), (0.3081,))
标准化(Normalization)
和基于决策树的机器学习模型,如RF、xgboost等不同的是,神经网络特别钟爱经过标准化处理后的数据。标准化处理指的是,data减去它的均值,再除以它的标准差,最终data将呈现均值为0方差为1的数据分布。决策树模型在哪里split特征是由特征序列决定的,跟具体数值无关,所以并不要求数据做标准化处理,至于详细原因以后有机会写机器学习博文时再详述。
神经网络模型偏爱标准化数据,原因是均值为0方差为1的数据在sigmoid、tanh经过激活函数后求导得到的导数很大,反之原始数据不仅分布不均(噪声大)而且数值通常都很大(本例中数值范围是0~255),激活函数后求导得到的导数则接近与0,这也被称为梯度消失。前文已经分析,神经网络是根据函数对权值求导的导数来调整权值,导数越大,调整幅度越大,越快逼近目标函数,反之,导数越小,调整幅度越小,所以说,数据的标准化有利于加快神经网络的训练。
除此之外,还需要保持train_set、val_set和test_set标准化系数的一致性。标准化系数就是计算要用到的均值和标准差,在本例中是((0.1307,), (0.3081,)),均值是0.1307,标准差是0.3081,这些系数都是数据集提供方计算好的数据,不同数据集就有不同的标准化系数,例如([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])就是Imagenet dataset的标准化系数(RGB三个通道对应三组系数),当需要将imagenet预训练的参数迁移到另一神经网络时,被迁移的神经网络就需要使用imagenet的系数,否则预训练不仅无法起到应有的作用甚至还会帮倒忙,例如,我们想要用神经网络来识别夜空中的星星,因为黑色是夜空的主旋律,从像素上看黑色就是数据集的均值,标准化操作时,所有图像会减去均值(黑色),如此Imagenet预训练的神经网络很难识别出这些数据是夜空图像。
Model
class Flatten(nn.Module):
def __init__(self): super().__init__()
def forward(self, x): return x.view(x.size(0), -1)
model = nn.Sequential(
Flatten(),
nn.Linear(784, 10),
nn.LogSoftmax()
).to(device)
我构建的神经网络很简单,一个全链接层后面跟一个softmax分类器,这就是linearity + non-linearity的结构,softmax剔除线性计算结果中的负值,并将数值转化为概率。
Loss Function
def train(model, device, train_loader, optimizer, epoch):
......
loss = F.nll_loss(output, target)
loss.backward()
......
本例使用损失函数是F.nll_loss(),即Negative log likelihood function,也称为cross entropy。Cross entropy(CE)有两种类型,binary cross entropy(BCE)和categorical cross entropy。
binary cross entropy用于逻辑回归之类的二元分类问题,它的数学公式: − ( y l o g p + ( 1 − y ) l o g ( 1 − p ) ) -(ylog^p + (1-y)log^{(1-p)}) −(ylogp+(1−y)log(1−p)), y y y是ground true的分类标签, p p p是神经网络预测的概率。假如我们要识别猫和狗的图片,标签1代表狗,标签0代表猫,样本1预测90%的概率是猫,样本2预测10%的概率是狗,样本2预测20%的概率是狗。BCE的计算结果如下表所示,不管目标是猫还是狗,都会可以用 − y l o g p -ylog^p −ylogp来计算。
| 猫(0) | 狗(1) | p | BCE |
|---|---|---|---|
| 0 | 1 | 0.9 | − l o g 0.9 -log^{0.9} −log0.9 |
| 1 | 0 | 0.1 | − l o g 0.9 -log^{0.9} −log0.9 |
| 1 | 0 | 0.2 | − l o g 0.8 -log^{0.8} −log0.8 |
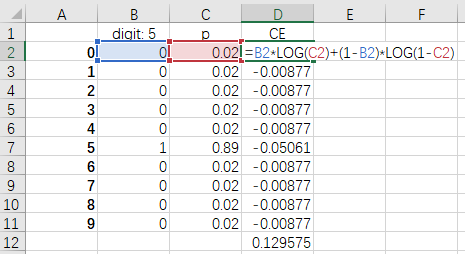
categorical cross entropy则不只有两个分类,本例中有10个分类,如Figure 3所示,一个ground true标签是一个长度为10的向量,同时也一次预测出10个结果,最终CE是10个BCE结果的总和:0.129575。
Training
lr = 1e-2
epochs = 10
torch.manual_seed(40)
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=0.9)
for epoch in range(1, epochs + 1):
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
本例使用SGD优化器来训练神经网络,而优化器是神经网络的重要模块,我打算在后续专门写一篇关于SGD和Adam的博文,因此这里先按下不表。你只需要理解优化器的作用就是通过loss值对神经元的参数求导并根据导数来调整个神经元参数即可。
Test set: Average loss: 0.2803, Accuracy: 9218/10000 (92%)
经过10个epoch的训练后,神经网络的表现是数字体识别的准确率为92%。要提高识别准确率,可以从神经网络规模、训练方法(学习率、优化器、epoch数量等)以及选取更合适的损失函数这几方面入手。
总结
神经网络是一种无限灵活的函数,只要它足够大,它可以逼近任意函数,找到解决难题对应的数学模型。
Refences
- A visual proof that neural nets can compute any function
- Pytorch MNIST sample