数字信号与图像处理
包括数字信号采样、fft、恢复、音频和图像的最最基本操作
这些操作用matlab更容易实现,现给出python3.5的实现版本
第一题
- A:试生成一个抽样频率为8k的信号序列,比如Matlab的Sinc波 Sinc或任何函数x 2 等, 说明它是否是声音,可用sound函数。
- B:编一首你喜欢简单的曲目,利用sound演示。
- C:读取一个图像并显示;
- D:利用矩阵块操作改变图像的像素,显示改变的结果。
import numpy as np
import math
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)A:试生成一个抽样频率为8k的信号序列,比如Matlab的Sinc波 Sinc或任何函数x 2 等, 说明它是否是声音,可用sound函数.
# 生成频率为K,幅值为A,长度为time_s,采样频率为s的信号序列
def signal(A,K,time_s,s):
return A * np.sin(np.linspace(0, K * time_s * 2 * np.pi, s* time_s))
signal = signal(1,44100,10,8000)len(signal) #在10秒中采样80,000个点80000# 绘制0.5%的信号图像
time = np.arange(1,len(signal)+1)/len(signal)
plt.figure(figsize=(15,3))
plt.plot(time[1:401],signal[1:401])
plt.xlabel("Time(s)")
plt.ylabel("Amplitude")
plt.title("Single channel data")
plt.grid('on')![]()
这是声音,因为波动都是声音,但不在人类分辨的频率范围内,抽样前过高(44.1kHZ),抽样后过低(5.5Hz)
B:编一首你喜欢简单的曲目,利用sound演示。
# 播放声音
import pyaudio as au
import wave# 直接播放MP3
import time
import pygame
pygame.mixer.init()
filename = r"D:\迅雷下载\28793052.mp3"
print(str(filename))
filename = filename.encode('utf-8')
track = pygame.mixer.music.load(filename)
pygame.mixer.music.play()
time.sleep(10)
pygame.mixer.music.stop()D:\迅雷下载\28793052.mp3由于python的windows版本不支持直接对mp3格式进行处理,下面演示对wav文件进行处理
import pylab as pl
# 打开WAV文档
wavepath = r"C:\Users\Thinkpad\Desktop\that.wav"
def read_wav(wavepath,show): #show=1则展示,否则不展示
f = wave.open(wavepath, "rb")
# 读取格式信息
# (nchannels, sampwidth, framerate, nframes, comptype, compname)
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
# 读取波形数据
str_data = f.readframes(nframes)
f.close()
#将波形数据转换为数组
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data.shape = -1, 2
wave_data = wave_data.T
time = np.arange(0, nframes) * (1.0 / framerate)
if(show):
# 绘制波形
#pl.subplot(211)
plt.figure(figsize=(15,3))
pl.plot(time, wave_data[0])
#pl.subplot(212)
plt.figure(figsize=(15,3))
pl.plot(time, wave_data[1], c="g")
pl.xlabel("time (seconds)")
pl.show()
f.close()
return wave_data
wave_data = read_wav(wavepath,1)c:\users\thinkpad\miniconda3\envs\mlia\lib\site-packages\ipykernel_launcher.py:15: DeprecationWarning: The binary mode of fromstring is deprecated, as it behaves surprisingly on unicode inputs. Use frombuffer instead
from ipykernel import kernelapp as app生成音频(也可以随意创造数组,将wave_data替换为自己的数组即可)
# 写入音频
import os
import struct
#提取前800个音节并创造自己的音节,单通道
sounds = wave_data[0:1,0:800]
sounds *= 2
sounds = sounds.T
sounds = sounds/max(abs(sounds))
outfile = wavepath+'\\out1.wav'
outwave = wave.open(outfile, 'wb')#定义存储路径以及文件名
nchannels = 1
sampwidth = 2
fs = 8000
data_size = len(sounds)
framerate = int(fs)
nframes = data_size
comptype = "NONE"
compname = "not compressed"
outwave.setparams((nchannels, sampwidth, framerate, nframes,comptype, compname))
for v in sounds:
outwave.writeframes(struct.pack('h', int(v * 64000 / 2)))#outData:16位,-32767~32767,注意不要溢出
outwave.close()播放自己的音频
# 读取音频进行播放
plt.plot(sounds) #自我创造的音频,被存在同路径下out1.wav文件
def play_wav(filepath):
#wav文件读取
f = wave.open(filepath,'rb')
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
if(show)
#instantiate PyAudio
p = pyaudio.PyAudio()
#define stream chunk
chunk = 1024
#打开声音输出流
stream = p.open(format = p.get_format_from_width(sampwidth),channels = nchannels,rate = framerate, output = True)
#写声音输出流到声卡进行播放
data = f.readframes(chunk)
while True:
data = f.readframes(chunk)
if data == b'': break
stream.write(data)
f.close()
#stop stream
stream.stop_stream()
stream.close()
#close PyAudio
p.terminate()
file_ = outfile
play_wav(file_)[] ![]()
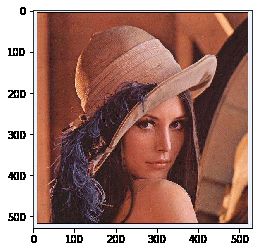
C:读取一个图像并显示
from PIL import Image
import numpy as np
# 输入图像路径
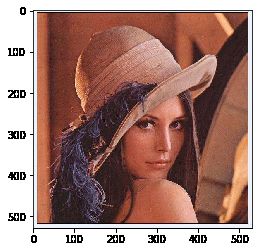
I = Image.open(r'C:\Users\Thinkpad\Desktop\lena.jpg')
I_array = np.array(I)
print("图像大小",I_array.shape)
plt.imshow(I_array,cmap='gray')图像大小 (528, 532, 3)
D:利用矩阵块操作改变图像的像素,显示改变的结果。
for i in range(50,200):
for j in range(50,200):
for k in range(0,1):
I_array[i,j,k] = int(I_array[i,j,k]/3)
plt.imshow(I_array,cmap='gray')
plt.savefig(r'C:\Users\Thinkpad\Desktop\lena_cut.png')# 采用1/2均值滤波对图像进行平滑处理
size = I_array.shape
per = 3
Trans = np.zeros(size) #创建一个存储变换数据的矩阵
for i in range(0,size[2]):
for j in range(per-1,size[0]-per+1):
for k in range(per-1,size[1]-per+1):
Trans[j][k][i] = I_array[j-2:j+3,k-2:k+3,i:i+1].sum() / (5*5) #对中心点周围per*per的矩阵内求均值
for i in range(0,size[2]):
I_array[:,:,i:i+1] = (I_array[:,:,i:i+1]+Trans[:,:,i:i+1])/2
plt.imshow(I_array)![]()
# 7/8均值滤波处理
i=0
while(i<2):
for i in range(0,size[2]):
I_array[:,:,i:i+1] = (I_array[:,:,i:i+1]+Trans[:,:,i:i+1])/2
i+=1
plt.imshow(I_array)第二题 选取任意信号,比如钢琴中央C键。
- A: 给出信号的时间延迟为1秒的对应信号。注意:不是y(n) = x(n − 1).
- B: 给出信号伸缩(λ = 2)的信号;
- C: 给出信号和Sinc波的乘积信号,卷积信号(利用conv);
- D: 说明A,B,C中信号的变化。可以用sound, 或fft。
A: 给出信号的时间延迟为1秒的对应信号。注意:不是y(n) = x(n − 1).
# 给出随机信号,长度为800,范围为0-1
random = np.random.rand(800)
plt.figure(figsize=(16,2))
plt.xlim(0,800)
plt.plot(random)
plt.title('生成的随机信号',fontproperties=font)Text(0.5, 1.0, '生成的随机信号')# 给出延迟信号x'(n)=x(n+1)并给出差值
random_=np.r_[[0],random[0:len(random)-1]]
plt.figure(figsize=(16,2))
plt.xlim(0,801)
pl.plot(random_,'orange')
plt.title('延迟信号',fontproperties=font)
plt.figure(figsize=(16,2))
plt.xlim(0,801)
delta = random[0:len(random)] - random_[0:len(random)]
pl.plot(delta,'green')
plt.title('信号差',fontproperties=font)Text(0.5, 1.0, '信号差')可以看出,延迟一秒就产生了巨大的变化
B: 给出信号伸缩(λ = 2)的信号;
#compress = random[]
plt.figure(figsize=(8,2))
xlim = np.arange(0,400,0.5)
plt.xlim(0,400)
pl.plot(xlim,random,'orange')
pl.title('压缩率为2',fontproperties=font)Text(0.5, 1.0, '压缩率为2')C: 给出信号和Sinc波的乘积信号,卷积信号(利用conv)
#由于python中只支持数值计算,不支持符号计算,因此给出[400,800]区间上的数值卷积(离散形式)
#生成sin信号
X = np.arange(401,801)
Sin = [math.sin(x) for i in X]
#计算卷积
Conv = np.convolve(random[400:801],Sin)
#画图
plt.figure(figsize=(16,8))
plt.xlim(200,1000)
plt.ylim(min(Conv),max(Conv))
Z = np.zeros(200)
Z = np.r_[Z,Conv]
plt.plot(Z,c='b')
pl.title('[400,800]区间数值卷积',fontproperties=font)Text(0.5, 1.0, '[400,800]区间数值卷积')![]()
明显看到,卷积不太平滑,但是基本和方波的卷积一致,这是因为我们生成的随机信号的服从均匀分布,均值为0.5
D: 说明A,B,C中信号的变化。可以用sound, 或fft。
A中信号向后平移1个单位,B中信号被压缩一倍,C中信号与sin进行了卷积(相当于sin作为一个滑窗从区间左端移到右端,计算滑窗内函数曲线重合的面积)
# 以FFT进行直观展示
from scipy.fftpack import fft
import seaborn
# 定义FFT绘图函数
def fastfourier(random,text):
if type(random)==list: #获取信号长度
L = len(random)
else:
L = random.shape[0]
rand_fft = fft(random) #快速傅里叶变换
rand_r = rand_fft.real # 获取实数部分
rand_i = rand_fft.imag # 获取虚数部分
RAND = abs(fft(random)) # 取模
rand = abs(fft(random)/(L/2)) #归一化处理
rand_half = rand[range(int(L/2))] #由于对称性,只取一半区间
#原始波形
plt.figure(figsize=(15, 10))
plt.subplot(221)
plt.plot(random)
plt.title('Original wave of '+text, fontproperties=font)
#混合波的FFT(双边频率范围)
plt.subplot(222)
plt.plot(RAND,'r') #显示原始信号的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range) of '+text, fontproperties=font)
#混合波的FFT(归一化)
plt.subplot(223)
plt.plot(rand,'g')
plt.title('FFT of Mixed wave(normalization) of '+text, fontproperties=font)
plt.subplot(224)
plt.plot(rand_half,'b')
plt.title('FFT of Mixed wave of '+text, fontproperties=font)
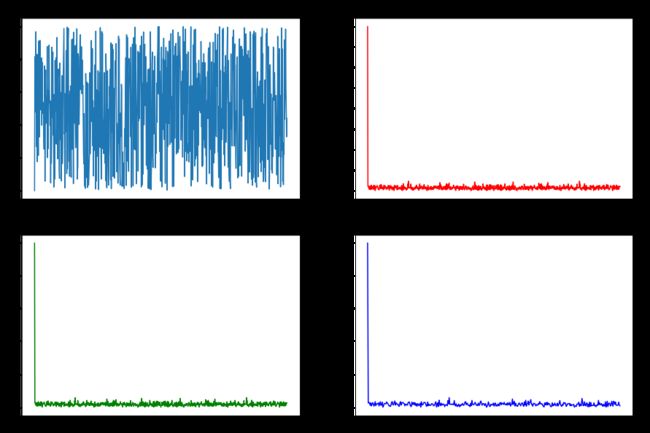
title_list = ['原始信号FFT','延迟信号FFT','卷积信号FFT','伸缩信号FFT']
signal_list = [random, random_, Z]
for i in range(0,3):
fastfourier(signal_list[i],title_list[i])![]()
第三题 (信号的调制)任选低频信号x(t),比如钢琴中央C键。
- A:利用高频信号(比如w 0 = 8Mhz),得到调制信号\(y(t) = x(t)cosw_0 t\)
- B:利用同样高频信号解调制,\(z(t) = y(t)cosw_0 t\)
- C:*** 利用低通滤波器回复信号\(x(t) = H(z(t))\).
- D:实现以上过程,并演示(sound or fft).
A:利用高频信号(比如\(w_0 = 8Mhz\)),得到调制信号\(y(t) = x(t)cosw_0 t\)
# 读取钢琴C键音频wav
# 文件夹中包含钢琴88键单音,中央C为第40个音,对应German Concert D 060 083.wav
middle_C = r'C:\Users\Thinkpad\Desktop\钢琴+88键\钢琴88\German Concert D 060 083.wav'
wave_C = read_wav(middle_C,1)c:\users\thinkpad\miniconda3\envs\mlia\lib\site-packages\ipykernel_launcher.py:15: DeprecationWarning: The binary mode of fromstring is deprecated, as it behaves surprisingly on unicode inputs. Use frombuffer instead
from ipykernel import kernelapp as app![]()
# 调解信号
trans_C = []
channel = wave_C.shape[0] #获取信道数量
len_C = wave_C.shape[1] #获取信号长度
for i in range(channel): #调制信号
trans_C.append([math.cos(8e6*t) for t in wave_C[i]])
plt.figure(figsize=(16,2))
plt.plot(trans_C[i][0:int(len_C/200)]) #展示前0.5%的信号
plt.title('调制信号第'+str(i+1)+'信道',fontproperties=font)B:利用同样高频信号解调制, ?(?)=?(?)????0?
# 再次调制
trans_C2 = []
for i in range(channel): #调制信号
trans_C2.append([math.cos(8e6*t) for t in trans_C[i]])
plt.figure(figsize=(16,2))
plt.plot(trans_C2[i][0:int(len_C/200)]) #展示前0.5%的信号
plt.title('调制信号第'+str(i+1)+'信道',fontproperties=font)![]()
C:*** 利用低通滤波器回复信号\(x(t) = H(z(t))\).
from scipy import signal
b, a = signal.butter(3, 2e-6, 'lowpass')
filtedData = signal.filtfilt(b, a, trans_C[0])
plt.figure(figsize=(16,2))
plt.plot(filtedData)
plt.title('第一次滤波的恢复',fontproperties=font)
b2, a2 = signal.butter(3, 2e-6, 'lowpass')
filtedData2 = signal.filtfilt(b2, a2, trans_C2[0])
plt.figure(figsize=(16,2))
plt.plot(filtedData2)
plt.title('第二次滤波的恢复',fontproperties=font)Text(0.5, 1.0, '第二次滤波的恢复')D:实现以上过程,并演示(sound or fft)
# FFT变换
fastfourier(np.array(trans_C[0][0:int(len_C/200)]), '第一次调制')
fastfourier(np.array(trans_C2[0][0:int(len_C/200)]), '第二次调制')第四题 学习并使用fft,ifft, 请选一个声音和图像文件演示。
#读取图像
from PIL import Image
import numpy as np
# 输入图像路径
I = Image.open(r'C:\Users\Thinkpad\Desktop\lena.jpg')
I_array = np.array(I)
print("图像大小",I_array.shape)
plt.imshow(I_array,cmap='gray')图像大小 (528, 532, 3)
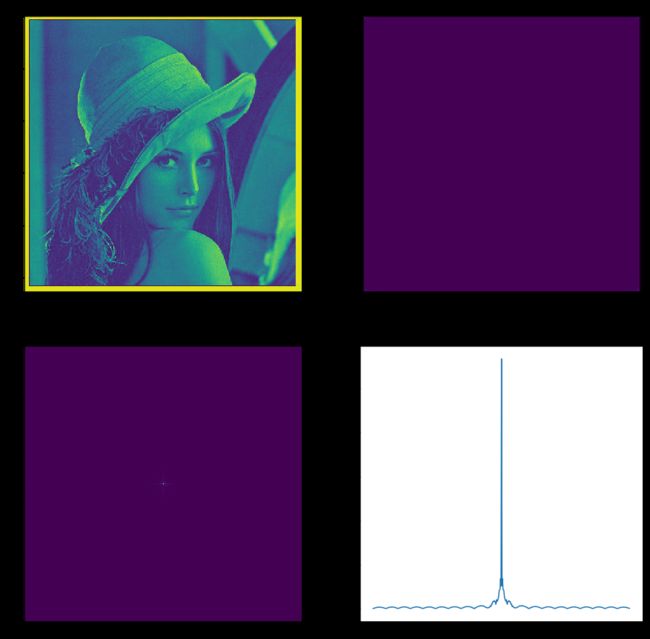
from scipy import fftpack
Z = plt.imread(r'C:\Users\Thinkpad\Desktop\lena.jpg')
# 转为灰度图
Z = 0.2126 * Z[:,:,0] + 0.7152 * Z[:,:,1] + 0.0722 * Z[:,:,2]
Z_fft2 = fftpack.fft2(Z)
Z_fft2_sh = abs(np.fft.fftshift(Z_fft2))
plt.figure(figsize=(15,15))
plt.subplot(221)
plt.imshow(Z)
plt.title('Original')
plt.subplot(222)
plt.imshow(abs(Z_fft2))
plt.title('fft2')
plt.subplot(223)
plt.imshow(Z_fft2_sh)
plt.title('fft2-shift')
plt.subplot(224)
plt.plot(Z_fft2_sh[int(I_array.shape[0]/2),:])
plt.title('x = 264')
plt.figure(figsize=(7,7))
Z_fft2_log = np.log(1 + np.abs(Z_fft2))
plt.plot(225)
plt.imshow(abs(Z_fft2_log))
plt.title('log_fft2')Text(0.5, 1.0, 'log_fft2')# 傅里叶逆变换
plt.figure(figsize=(7,7))
Z_ifft2 = fftpack.ifft2(Z_fft2)
plt.plot()
plt.imshow(abs(Z_ifft2))
plt.title('ifft2逆变换',fontproperties=font)Text(0.5, 1.0, 'ifft2逆变换')# 读取音频信号
middle_C = r'C:\Users\Thinkpad\Desktop\钢琴+88键\钢琴88\German Concert D 060 083.wav'
wave_C = read_wav(middle_C,1)
# fft变换
W = wave_C
W = np.fft.fft(W)
W = W.astype(np.uint8)
Wi = np.fft.ifft(W)
Wi = Wi.astype(np.uint8)
plt.figure(figsize=(15,15))
plt.subplot(221)
pl.imshow(W)
plt.title('fft')
plt.subplot(222)
plt.imshow(Wi)
pl.title('ifft')c:\users\thinkpad\miniconda3\envs\mlia\lib\site-packages\ipykernel_launcher.py:15: DeprecationWarning: The binary mode of fromstring is deprecated, as it behaves surprisingly on unicode inputs. Use frombuffer instead
from ipykernel import kernelapp as app![]()
c:\users\thinkpad\miniconda3\envs\mlia\lib\site-packages\ipykernel_launcher.py:8: ComplexWarning: Casting complex values to real discards the imaginary part
c:\users\thinkpad\miniconda3\envs\mlia\lib\site-packages\ipykernel_launcher.py:10: ComplexWarning: Casting complex values to real discards the imaginary part
# Remove the CWD from sys.path while we load stuff.
Text(0.5, 1.0, 'ifft')![]()
第五题 (模拟演示时域的抽样定理)
- A: 构造一个频率有限的信号(可取若干个正弦信号的和)
- B: 使用三种抽样频率(Nyquist频率,过抽样和欠抽样频率)进行抽样.利用sound说明信号的变化,给出对应信号的频谱(fft),并比较.
- C:说明并构造混叠现象。
- D: ***尝试从抽样信号恢复原信号(可以用滤波器filter);
A: 构造一个频率有限的信号(可取若干个正弦信号的和)
# 构造正弦叠加信号,长度为1024,展示在B中
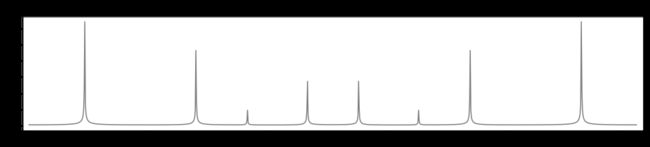
Y = lambda X: [0.7*math.sin(10*xx) + 0.5*math.sin(30*xx) + 0.3*math.sin(50*xx) + 0.1*math.sin(70*xx) for xx in X]B: 使用三种抽样频率(Nyquist频率,过抽样和欠抽样频率)进行抽样.利用sound说明信号的变化,给出对应信号的频谱(fft),并比较.
# 数学计算得信号的频率为70/2pi,为了计算简便取为70,Nyquist频率为170
def samplef(w,txt,color,sign,fft,fftsh,return_):
#sign,fft,fftsh分别控制是否显示信号图、FFT图、频谱图,return_控制是否返回信号值
x_sample = np.linspace(1,int(1024 * w/70),1024) #信号生成函数
signal = Y(x_sample)
if(sign):
plt.figure(figsize=(16,3))
plt.xlim(-10,1034)
plt.plot(signal,c=color)
plt.title(txt,fontproperties=font)
y_fft = np.fft.fft(signal)
if(fft):
plt.figure(figsize=(16,3))
plt.xlim(-10,1034)
plt.plot(y_fft,c=color)
plt.title(txt+'FFT',fontproperties=font)
y_fft_sh = abs(np.fft.fftshift(y_fft))
if(fftsh):
plt.figure(figsize=(16,3))
plt.xlim(-10,1034)
plt.plot(y_fft_sh,c=color)
plt.title(txt+'频谱图',fontproperties=font)
if(return_):
return x_sample,signal,y_fft,y_fft_sh # 依次返回采样点、采样点函数值、FFT变换、频谱
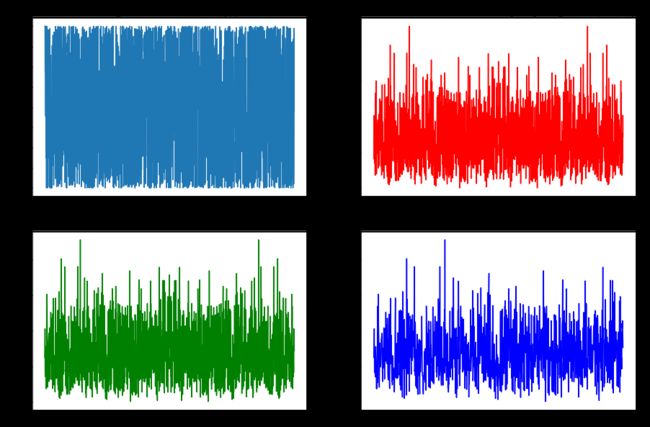
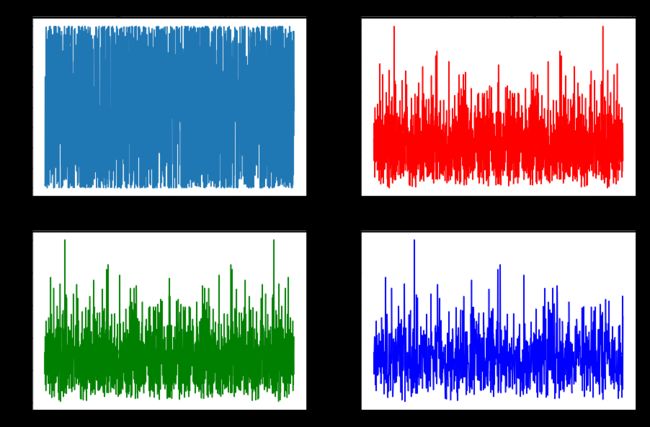
# 原始信号
samplef(70,'原始信号','orange',1,0,0,0)
# Nyquist抽样 wn = 210
samplef(140,'Nyquist抽样信号','g',1,1,0,0)
# 过抽样 w1 = 512
samplef(280,'4倍频过采样','r',1,1,0,0)
# 欠抽样 w2 = 70
samplef(35,'1/2倍频欠采样','b',1,1,0,0)![]()
![]()
![]()
![]()
![]()
C:说明并构造混叠现象。
'''
混叠是指取样信号被还原成连续信号时产生彼此交叠而失真的现象。
当混叠发生时,原始信号无法从取样信号还原。而混叠可能发生在时域上,称做时间混叠,或是发生在频域上,被称作空间混叠。
'''
samplef(105,'信号混叠','g',1,1,1,0)
samplef(70,'原始信号','grey',0,0,1,0)![]()
![]()
![]()
对比频谱图可知发生了混叠现象,信号峰发生了位移和加强
D: ***尝试从抽样信号恢复原信号(可以用滤波器filter).
from scipy import signal
# 获取采样信号
_,signal1,_,_ = samplef(140,'Nyquist抽样信号','g',0,0,0,1)
_,signal2,_,_ = samplef(280,'4倍频抽样信号','b',0,0,0,1)
_,signal3,_,_ = samplef(35,'1/2倍频抽样信号','b',0,0,0,1)
# 滤波器
def recover(signal_,w0,times,title,type_,color):
#w0为滤波频率,times为滤波次数,type_为滤波模式{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}
b, a = signal.butter(1, w0, type_)
recover = signal.filtfilt(b, a, signal_)
plt.figure(figsize=(16,3))
plt.plot(recover,c=color)
plt.xlim(10,1024)
# plt.ylim(-0.25,0.25)
plt.title(title,fontproperties=font)
# 低通
recover(signal1,2*69/140,1,'Nyquist低通滤波恢复','lowpass','b')
recover(signal2,2*69/280,1,'4倍频采样低通滤波恢复','lowpass','b')
recover(signal3,2*10/35,1,'1/2倍频采样低通滤波恢复','lowpass','b')
# 带通
recover(signal1,[2*10/140,2*69/140],1,'Nyquist带通滤波恢复','bandpass','g')
recover(signal2,[2*10/280,2*69/280],1,'4倍频采样带通滤波恢复','bandpass','g')
recover(signal3,[2*9/35,2*17/35],1,'1/2倍频采样带通滤波恢复','bandpass','g')
# 高通
recover(signal1,2*10/140,1,'Nyquist高通滤波恢复','highpass','r')
recover(signal2,2*10/280,1,'4倍频采样高通滤波恢复','highpass','r')
recover(signal3,2*10/35,1,'1/2倍频采样高通滤波恢复','highpass','r')
![]()
![]()
![]()
![]()